Прямоугольная (декартова) система координат в пространстве. Формулы середины отрезка и расстояния между двумя точками

1.

Прямоугольная (декартова)
система координат в
пространстве.
Формулы середины отрезка и
расстояния между двумя точками.

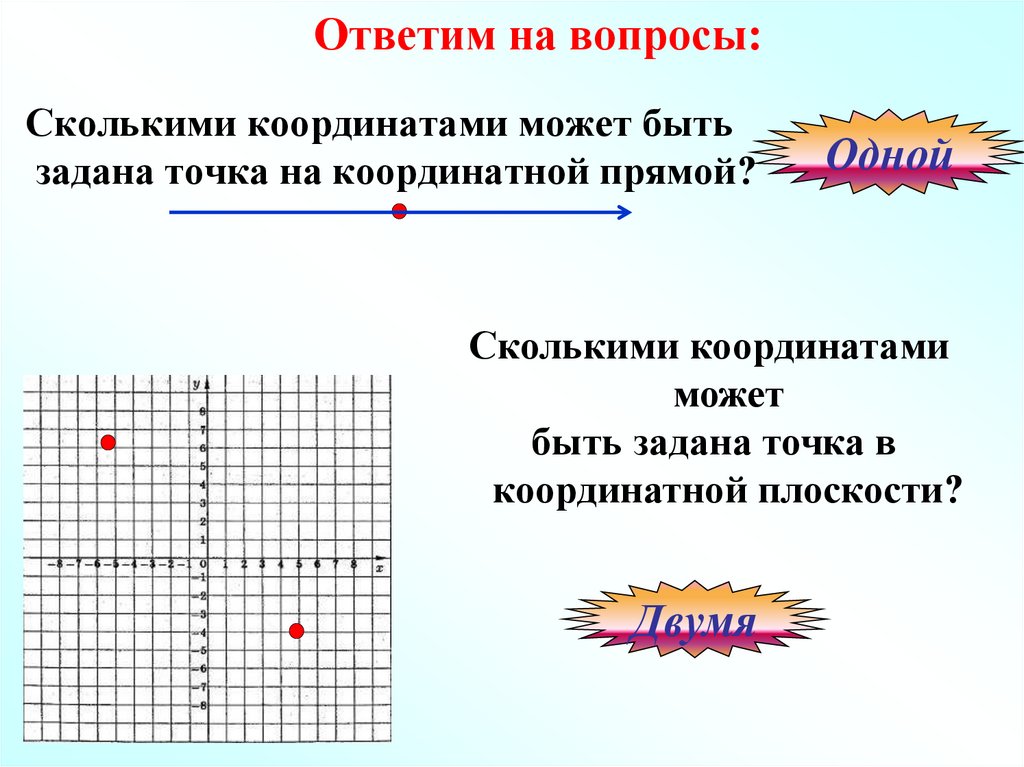
2. Ответим на вопросы:

Сколькими координатами может быть
задана точка на координатной прямой?
Одной
Сколькими координатами
может
быть задана точка в
координатной плоскости?
Двумя

3.

Вспомним, как определяется координатная(числовая) прямая.
1) Изображаем произвольную прямую;
2) Придаем ей положительное направление и обозначаем её;
3) Выбираем произвольную точку за начало отсчета;
4) Определяем длину единичного отрезка (масштаб).
М
х
0
1
а
Тогда любой точки этой координатной прямой соответствует
единственное действительное число a. И наоборот, любое
действительное число может быть изображено единственной
соответствующей точкой, для которой это число является
координатой. Записывают: M(a).

4.

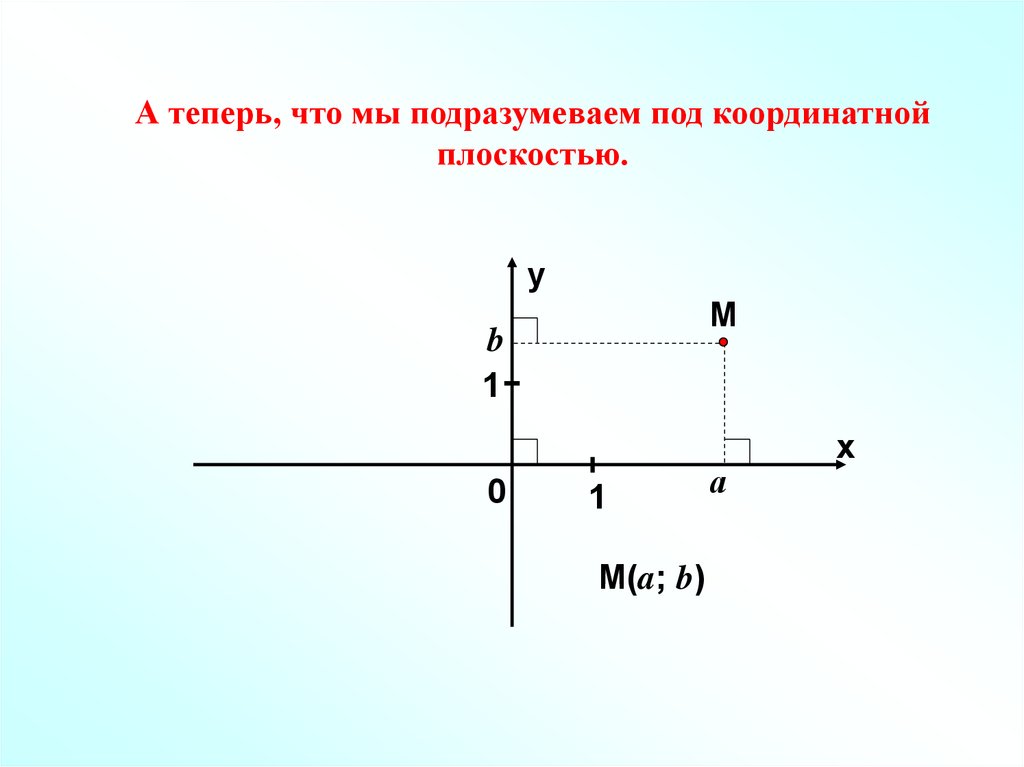
А теперь, что мы подразумеваем под координатной
плоскостью.
у
М
b
1
0
1
M(a; b)
а
х

5.

Сколькими
координатами может
быть задана точка в
пространстве?

6.

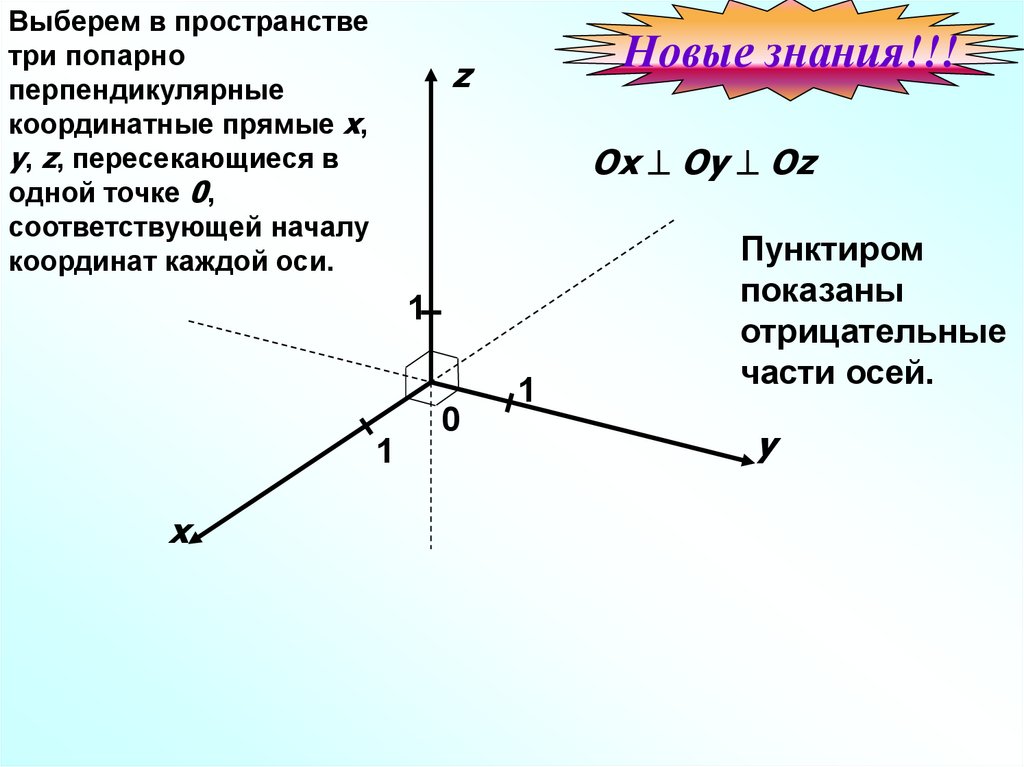
Выберем в пространстве
три попарно
перпендикулярные
координатные прямые x,
y, z, пересекающиеся в
одной точке 0,
соответствующей началу
координат каждой оси.
Новые знания!!!
z
Ox Oy Oz
1
0
1
x
1
Пунктиром
показаны
отрицательные
части осей.
y

7.

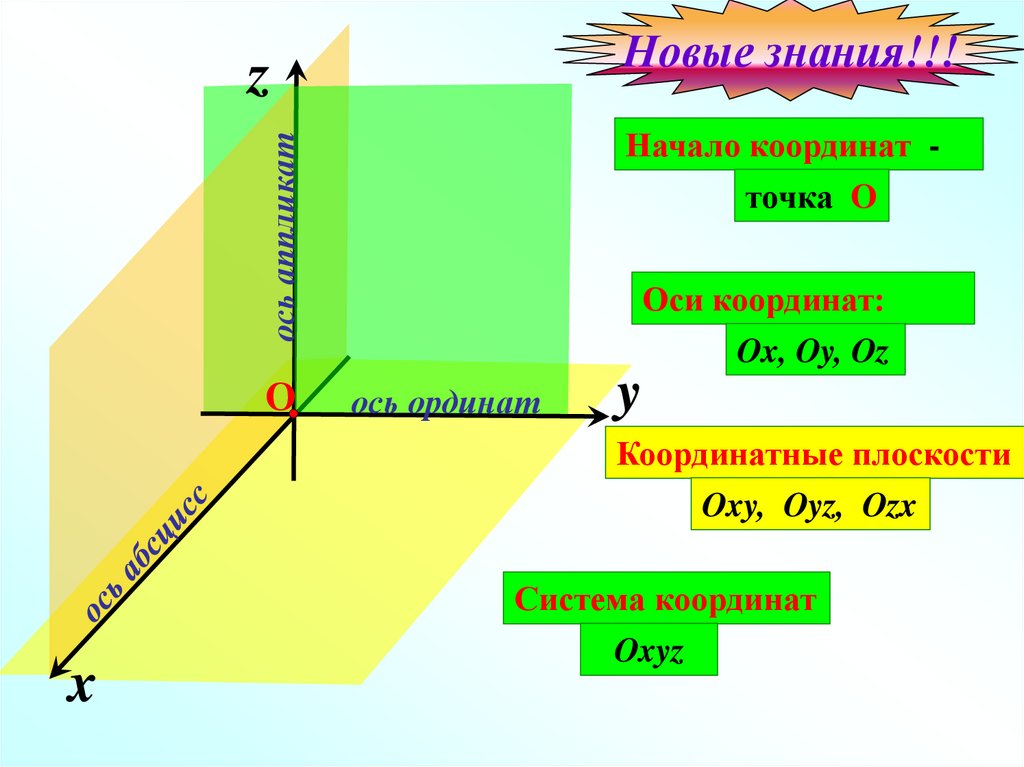
Новые знания!!!
z
ось аппликат
Начало координат -
О
точка O
Оси координат:
Ox, Oy, Oz
ось ординат
y
Координатные плоскости
Oxy, Oyz, Ozx
x
Система координат
Oxyz

8.

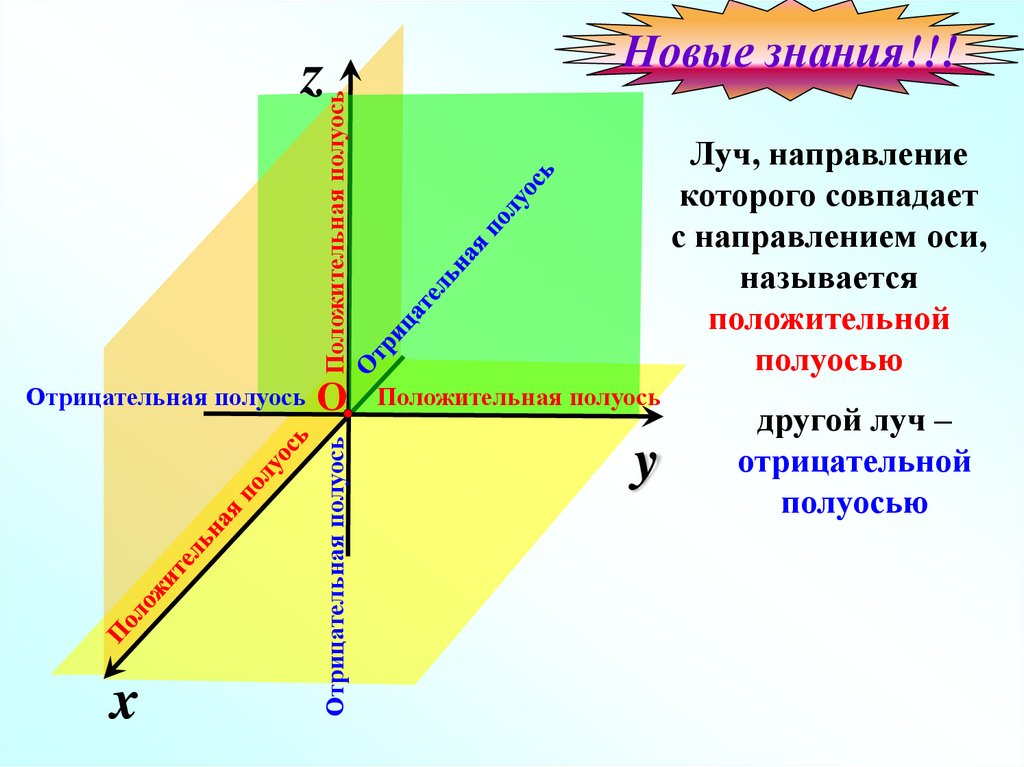
Положительная полуось
z
Новые знания!!!
Отрицательная полуось О
Положительная полуось
Отрицательная полуось
Луч, направление
которого совпадает
с направлением оси,
называется
положительной
полуосью
y
x
другой луч –
отрицательной
полуосью

9.

Новые знания!!!
z
M3
M
О
M1
x
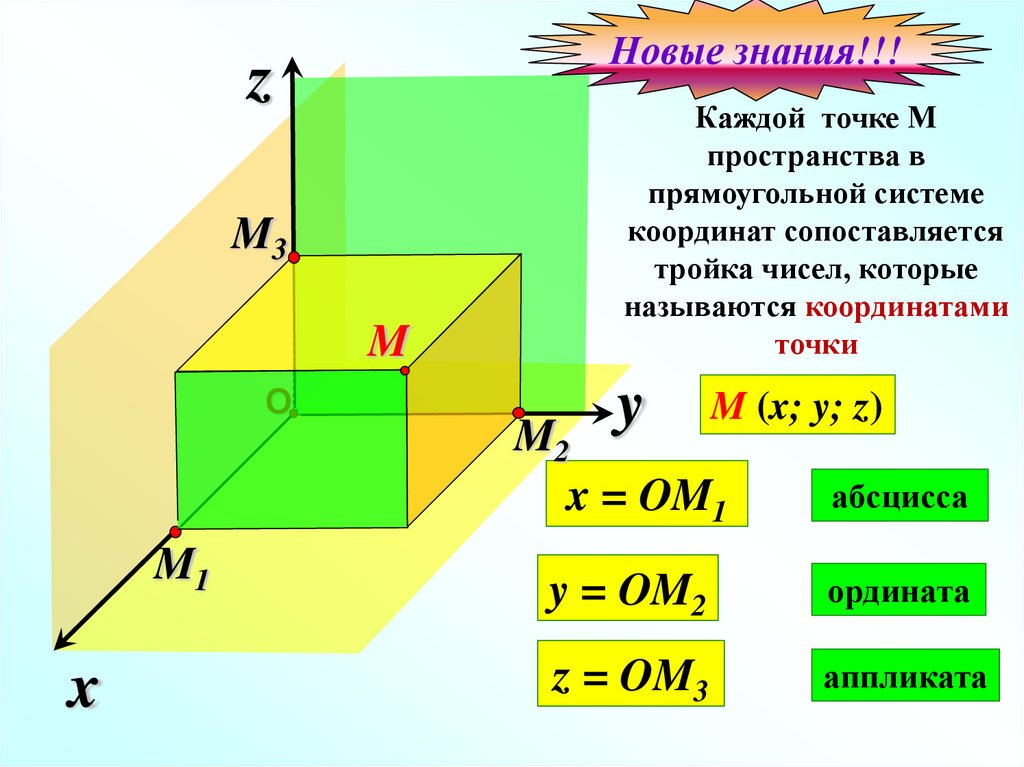
Каждой точке М
пространства в
прямоугольной системе
координат сопоставляется
тройка чисел, которые
называются координатами
точки
y
M (x; y; z)
M2
x = OM1
абсцисса
y = OM2
ордината
z = OM3
аппликата

10.

z
Новые знания!!!
I
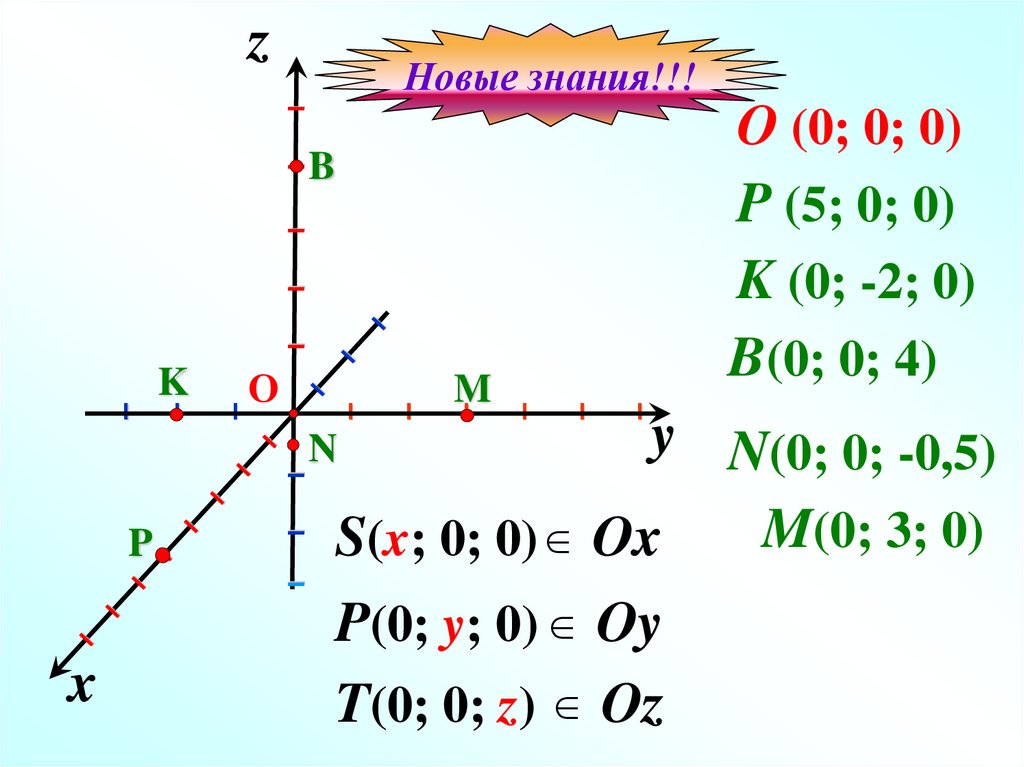
O (0; 0; 0)
P (5; 0; 0)
K (0; -2; 0)
B(0; 0; 4)
I
I
I
I
B
I
K
I
I
О
I
I
M
I
I
I
I
y N(0; 0; -0,5)
M(0; 3; 0)
S(x; 0; 0) Ox
I
P
I
I
N
x
P(0; y; 0) Oy
T(0; 0; z) Oz

11.

z
I
Новые знания!!!
A
I
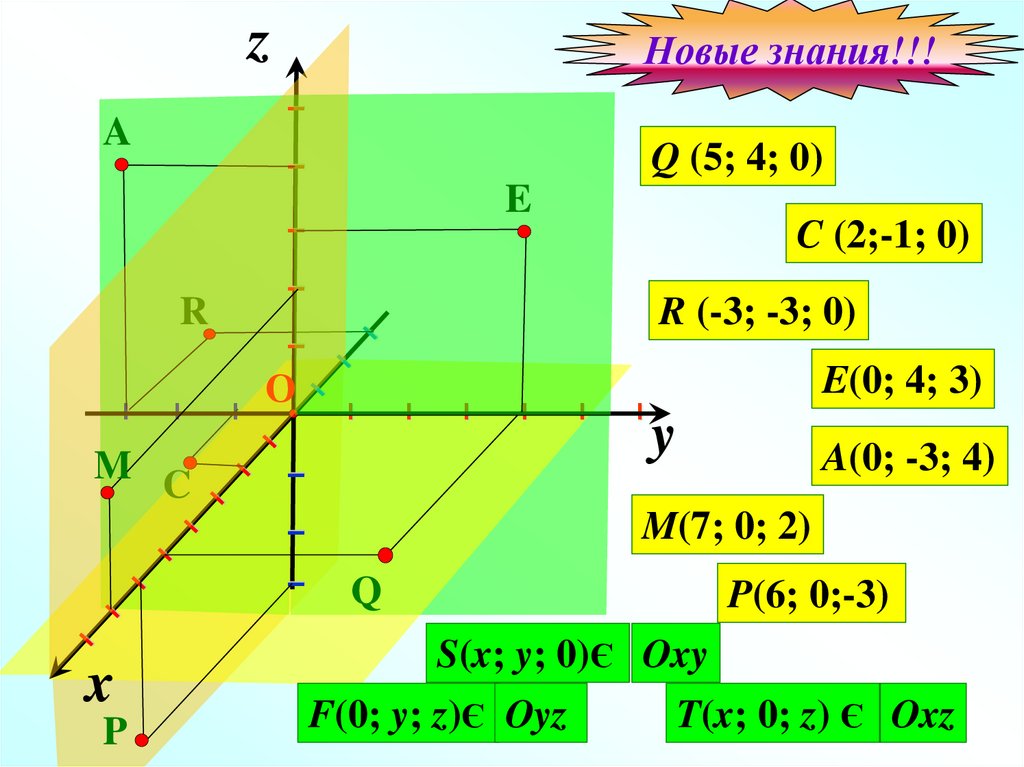
Q (5; 4; 0)
E
I
I
C (2;-1; 0)
R (-3; -3; 0)
I
R
I
I
I
I
I
x
P
I
I
y
A(0; -3; 4)
M(7; 0; 2)
I
M C
I
I
I
E(0; 4; 3)
О
I
Q
P(6; 0;-3)
S(x; y; 0)Є Oxy
F(0; y; z)Є Oyz
T(x; 0; z) Є Oxz

12.

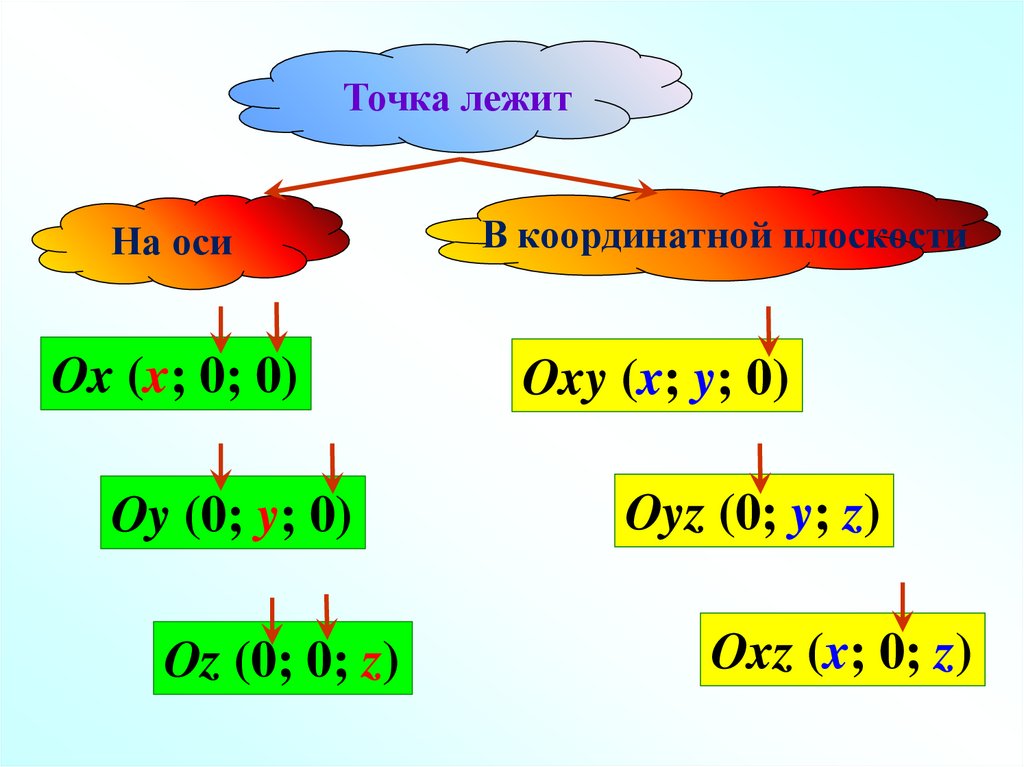
Точка лежит
На оси
Ox (x; 0; 0)
Oy (0; y; 0)
Oz (0; 0; z)
В координатной плоскости
Oxy (x; y; 0)
Oyz (0; y; z)
Oxz (x; 0; z)

13.

z
S
I
R
N
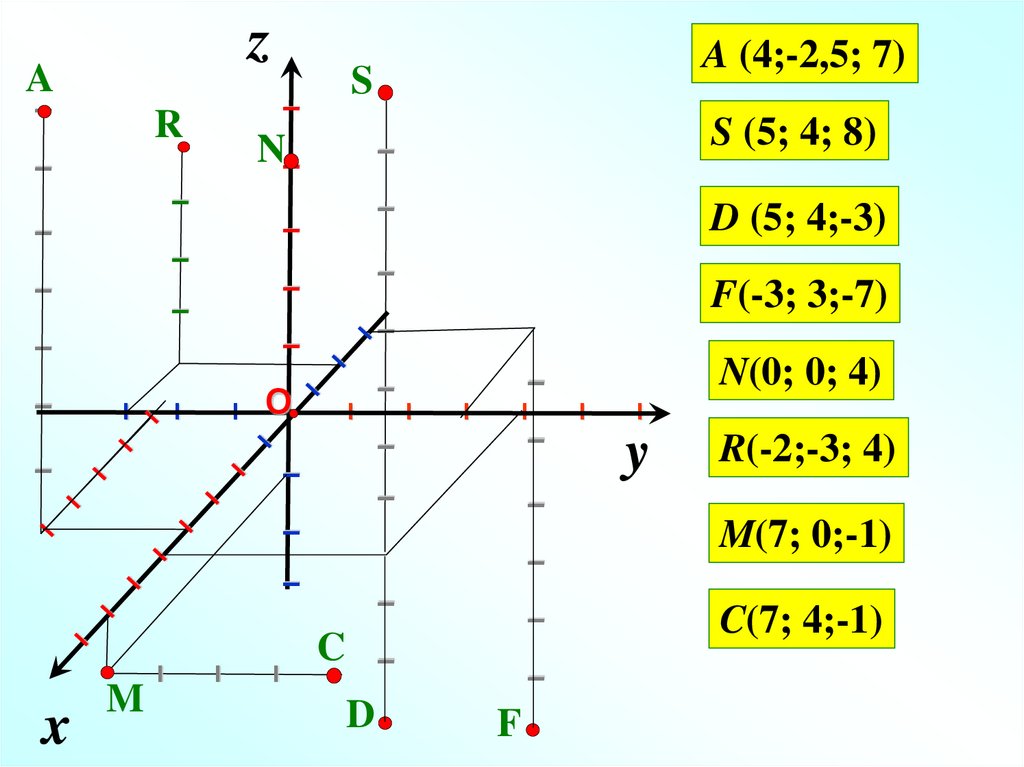
S (5; 4; 8)
I
I
I
I
I
A
A (4;-2,5; 7)
I
I
I
I
I
D (5; 4;-3)
I
I
I
I
I
I
I
I
y
R(-2;-3; 4)
I
I
I
I
N(0; 0; 4)
I
I
О
I
I
I
I
I
I
I
I
I
I
F(-3; 3;-7)
I
I
I
I
I
M(7; 0;-1)
x
M
I
I
I
I
I
C
D
F
C(7; 4;-1)

14.

Решение задач
Точки
и С рассмотреть
№ 401
(а) ВРассмотрим
точкусамостоятельно
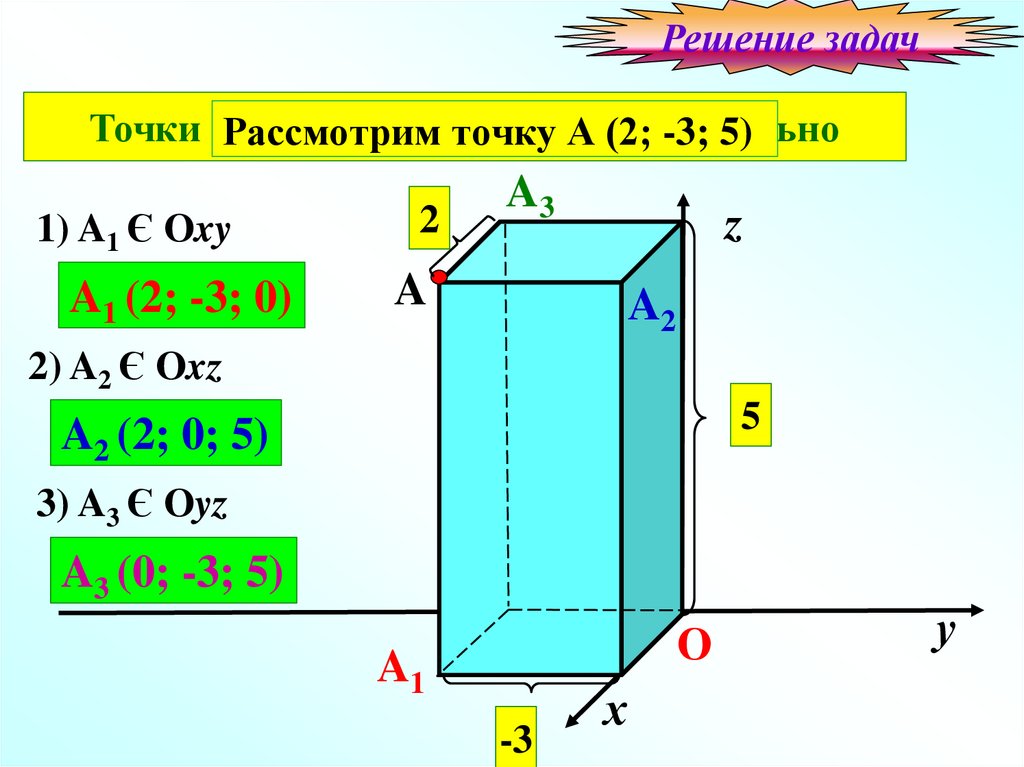
А (2; -3; 5)
1) A1 Є Oxy
A1 (2; -3; 0)
2
A3
z
A
A2
2) A2 Є Oxz
5
A2 (2; 0; 5)
3) A3 Є Oyz
A3 (0; -3; 5)
О
A1
-3
х
у

15.

№Точки
401 (б)В иРассмотрим
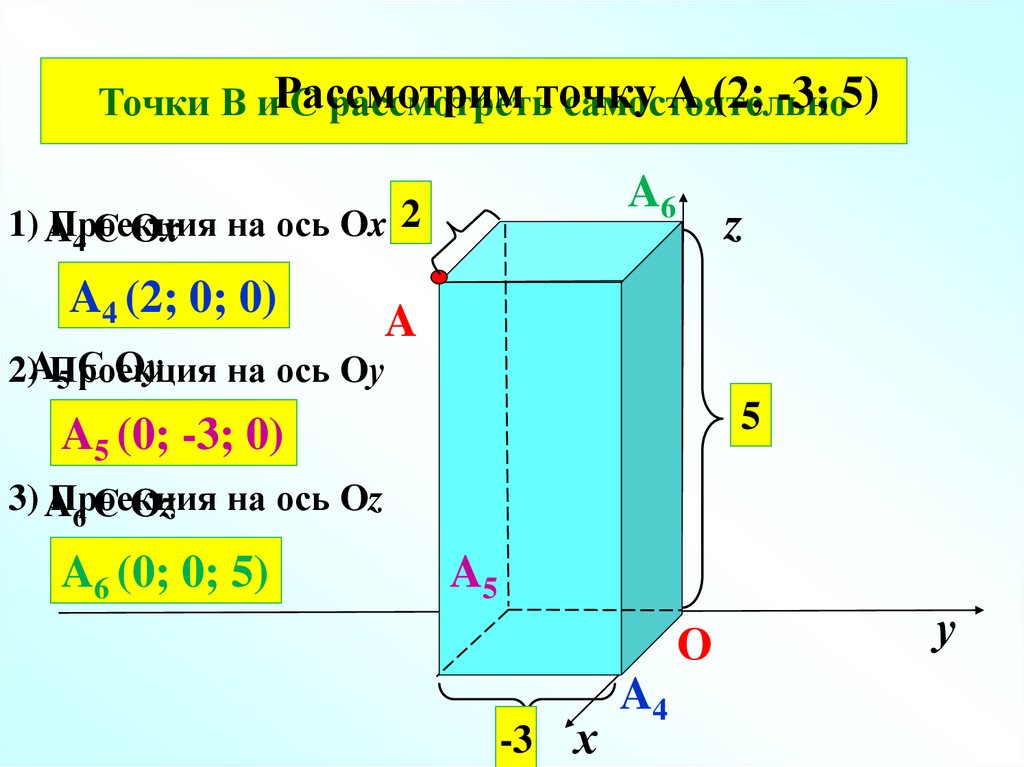
А (2; -3; 5)
С рассмотретьточку
самостоятельно
A6
2
1) A
Проекция
на
ось
Ox
Є
Ox
4
A4 (2; 0; 0)
z
A
2)AПроекция
на ось Oу
5 Є Oу
5
A5 (0; -3; 0)
3) A
Проекция
на ось Oz
6 Є Oz
A6 (0; 0; 5)
A5
О
-3
х
A4
у

16.

Расстояние между точками A(x1; y1; z1) и B(x2; y2; z2)
АВ
x2 x1 y2 y1 z2 z1
2
2
2
Координаты середины отрезка АВ, где A(x1; y1; z1) и B(x2; y2; z2)
x1 x2 y1 y2 z1 z2
M
;
;
2
2
2

17. Задача

Решение задач
Дано: А (1;-1;2), В (3;1;-2)
Найдите координаты
середины отрезка АВ и
его длину.

18. Решите задачи

Решение задач
Решите задачи
1) Дано: А (1;-1;2), В (3;1;-2)
Найдите координаты середины отрезка АВ и его длину.
2) № 424 (б)
3) № 425 (а)
Оформите решение задач в соответствии с требованиями
УДАЧИ!