Similar presentations:
Прямоугольная система координат в пространстве
1. Прямоугольная система координат в пространстве
2.
- Вы уже знакомы с прямоугольной(Декартовой) системой координат на
плоскости, которую
в XIX в. ввёл
французский
математик
Рене Декарт
3.
- А, вот, прямоугольную системукоординат в пространстве ввёл
швейцарский,
немецкий,
российский
математик
Леонард Эйлер
в XVIIIв.
4.
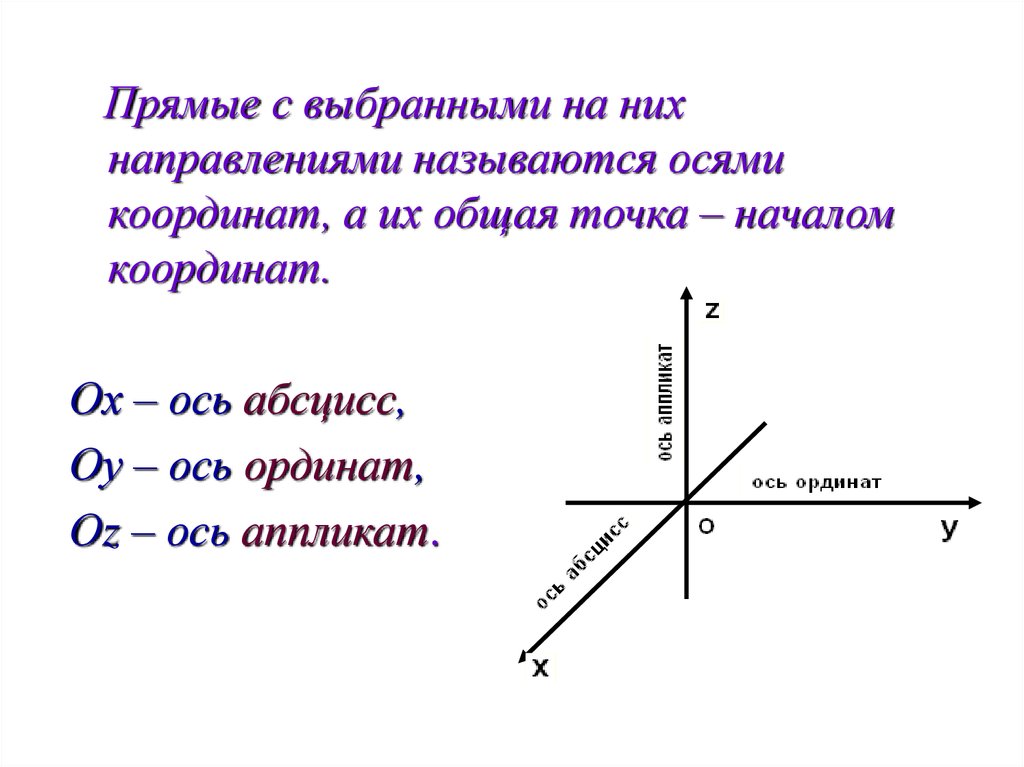
Прямые с выбранными на нихнаправлениями называются осями
координат, а их общая точка – началом
координат.
Ох – ось абсцисс,
Оу – ось ординат,
Оz – ось аппликат.
5.
Три плоскости, проходящие через осикоординат Ох и Оу, Оу и Оz, Оz и Ох,
называются координатными плоскостями:
Оху, Оуz, Оxz.
Плоскость Oyz
Плоскость Oxz
O
Плоскость Oxy
6.
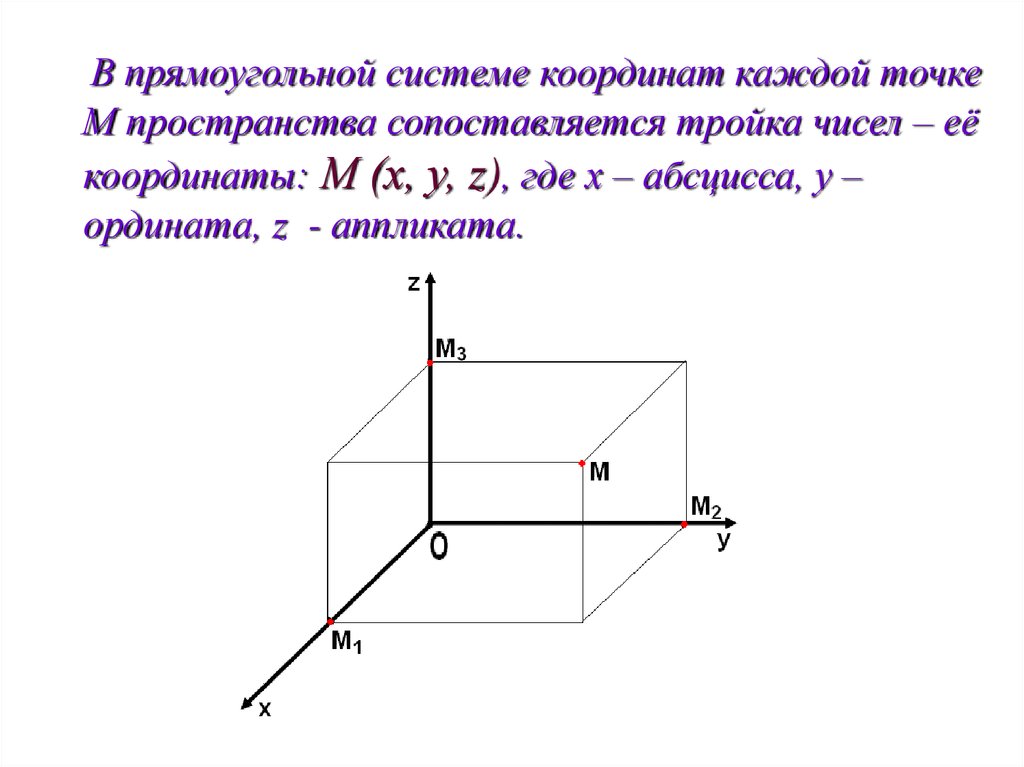
В прямоугольной системе координат каждой точкеМ пространства сопоставляется тройка чисел – её
координаты: М (х, у, z), где х – абсцисса, у –
ордината, z - аппликата.
7. Нахождение точки на координатной плоскости.
Если, например, точка M лежит на координатной плоскостиили на оси координат, то некоторые её координаты равны
нулю. Так, если M принадлежит Oxy, то аппликата точка M
равна нулю: z=0. Аналогично если M принадлежит Oхz, то
y=0, а если M принадлежит Oyz, то x=0. Если M
принадлежит Ox, то ордината и аппликата точки M равна
нулю: y=0 и z=0. Если M принадлежит Oy, то x=0 и z=0;
если M принадлежит Oz, то x=0 и y=0. Все три координаты
начала координат равны нулю: О (0;0;0).
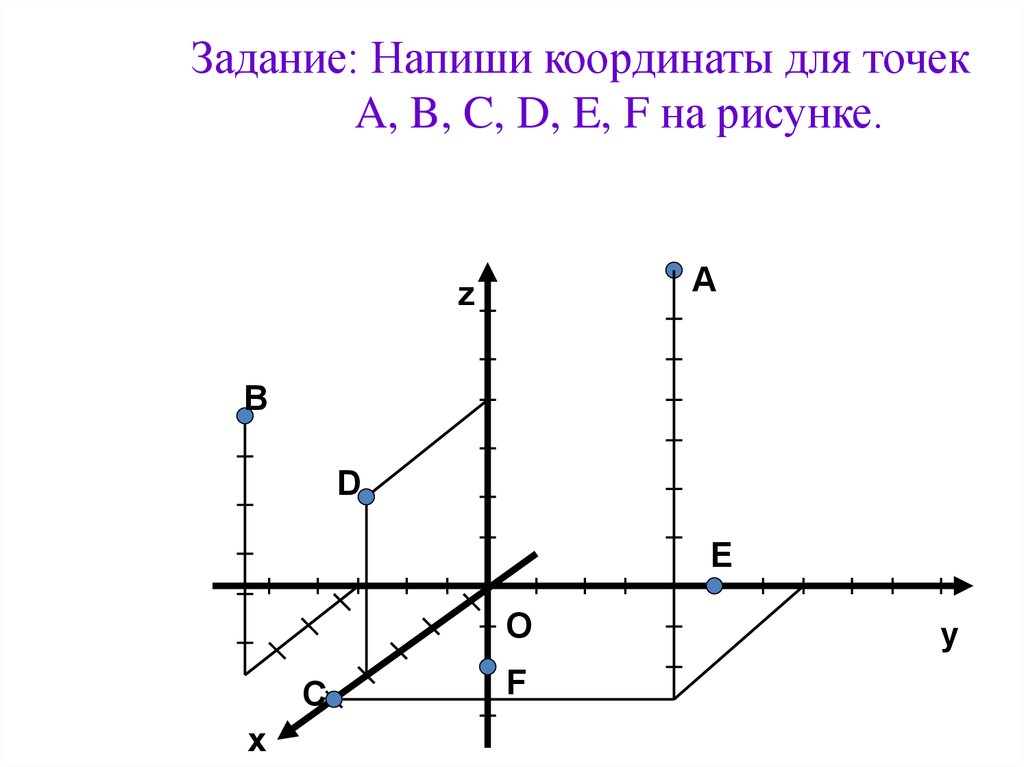
8. Задание: Напиши координаты для точек A, B, C, D, E, F на рисунке.
Az
B
D
E
O
C
x
F
y
9. Ответы
1. A(5; 4; 10),2. B(4; -3; 6),
3. C(5; 0; 0),
4. D(4; 0; 4),
5. E(0; 5; 0),
6. F(0; 0; -2).
Сравни свои ответы.
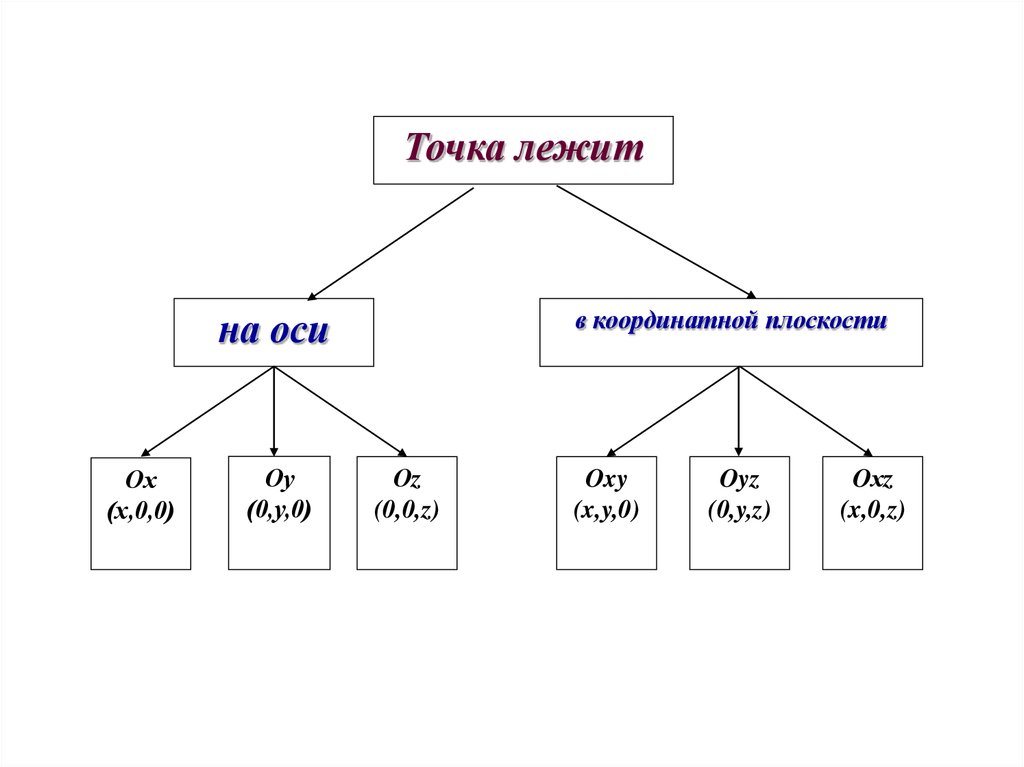
10.
Точка лежитв координатной плоскости
на оси
Ох
(х,0,0)
Оу
(0,у,0)
Оz
(0,0,z)
Oxy
(x,y,0)
Oyz
(0,y,z)
Oхz
(x,0,z)
11.
Нахождение точки на координатнойплоскости.
1. Если М
2. Если М
3. Если М
4. Если М
5. Если М
6. Если М
ОХУ, то z=0
OXZ, то у=0
OУZ, то X=0
ОХ, то У=0 и Z=0
OУ, то Х=0 и Z=0
OZ, то Х=0 и У=0
12.
Координаты вектора впространстве
13.
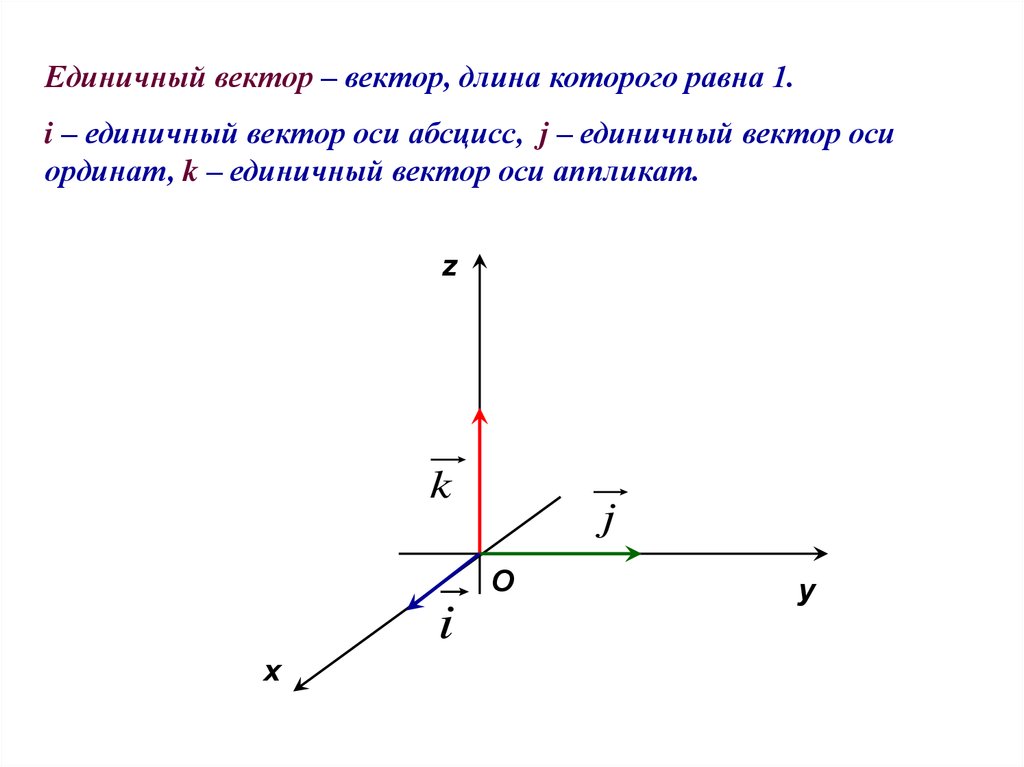
Единичный вектор – вектор, длина которого равна 1.i – единичный вектор оси абсцисс, j – единичный вектор оси
ординат, k – единичный вектор оси аппликат.
z
k
j
O
i
x
y
14.
Любой вектор ā можно разложить по координатнымвекторам, т.е. представить в виде:
а хi y j z k
Нулевой вектор можно представить в виде:
0 0i 0 j 0k
Координаты равных векторов соответственно равны,
т.е., если
ā { x1; y1; z1 } = b { x2; y2; z2 }, то
x1 = x2, y1 = y2, z1 = z2.
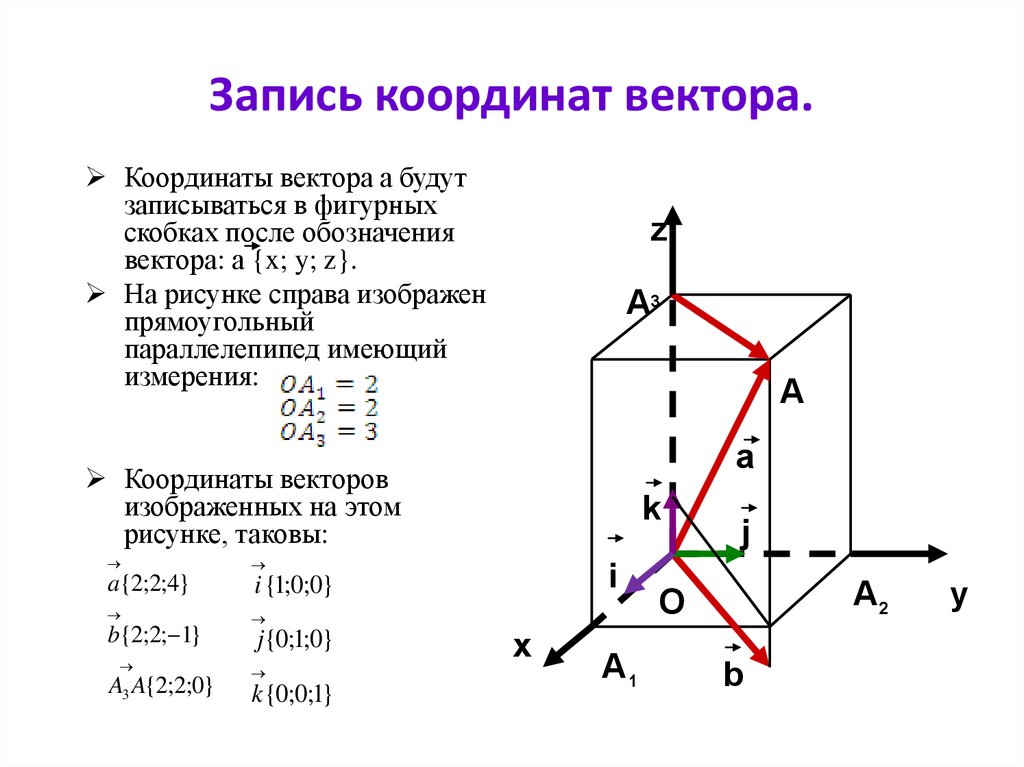
15. Запись координат вектора.
Координаты вектора а будутзаписываться в фигурных
скобках после обозначения
вектора: а {x; y; z}.
На рисунке справа изображен
прямоугольный
параллелепипед имеющий
измерения:
z
A3
A
a
Координаты векторов
изображенных на этом
рисунке, таковы:
a{2;2;4}
i {1;0;0}
b{2;2; 1}
A3 A{2;2;0}
j{0;1;0}
k {0;0;1}
k
i
x
A1
j
A2
O
b
y
16. Формулы середины отрезка и расстояния между точками на плоскости.
x1 x2 y1 y2М
;
2
2
АВ
x2 x1 y2 y1
2
2
17. Задача №1. Найдите координаты середины отрезка АВ и длину отрезка АВ, если:
1 вариант А (3;-1), В (-2;4)2 вариант А (3;4), В (2; -1)
18.
I вариантДано: А (3;-1), В (-2;4),
точка М – середина АВ.
Найти: IАВI, М(x;y).
Решение:
АВ
x2 x1 2 y2 y1 2
АВ
2 3 2 4 ( 1) 2
25 25
50 5 2
II вариант
Дано: А (3;4), В (2;-1),
точка С – середина АВ.
Найти: IАВI, С(x;y).
Решение:
АВ
x2 x1 2 y2 y1 2
АВ (2 3) 2 ( 1 4) 2 1 25 26
x x2 y1 y 2
М 1
;
2
2
x x2 y1 y 2
С 1
;
2
2
3 ( 2) 1 4
М
;
2
2
3 2 4 ( 1)
С
;
2
2
М 0,5;1,5
Ответ:
АВ 5 2
М 0,5;1,5
С 2,5;1,5
Ответ:
АВ 26
С 2,5;1,5
19.
Расстояние между точками A(x1; y1; z1) и B(x2; y2; z2)АВ
x2 x1 y2 y1 z2 z1
2
2
2
Координаты середины отрезка АВ, где A(x1; y1; z1) и B(x2; y2; z2)
x1 x2 y1 y2 z1 z2
M
;
;
2
2
2













 mathematics
mathematics








