Прямоугольная система координат в пространстве

1.

Прямоугольная
система
координат в
пространстве

2.

Цели урока
Знать: как изображать точку пространства по
ее координатам в прямоугольной системе
координат. .
Уметь: изображать точку пространства по ее
координатам в прямоугольной системе
координат; находить координаты проекции
точки пространства на координатные оси и
плоскости.

3.

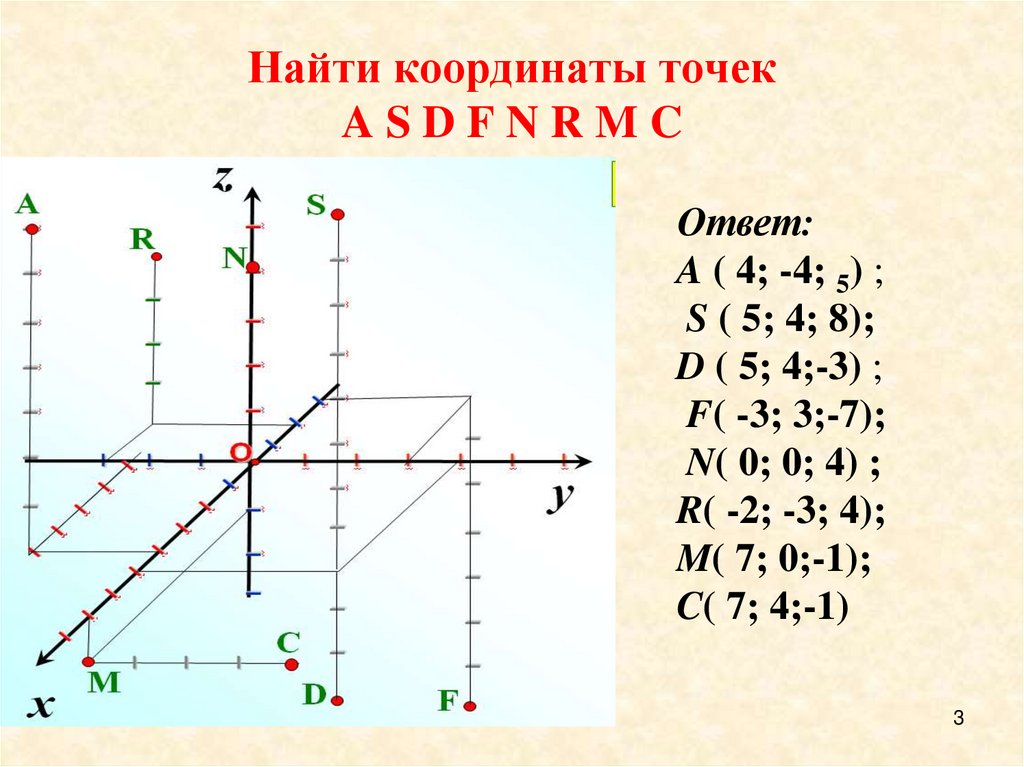
Найти координаты точек
ASDFNRMC
Ответ:
A ( 4; -4; 5) ;
S ( 5; 4; 8);
D ( 5; 4;-3) ;
F( -3; 3;-7);
N( 0; 0; 4) ;
R( -2; -3; 4);
M( 7; 0;-1);
C( 7; 4;-1)
04.02.2025
3

4.

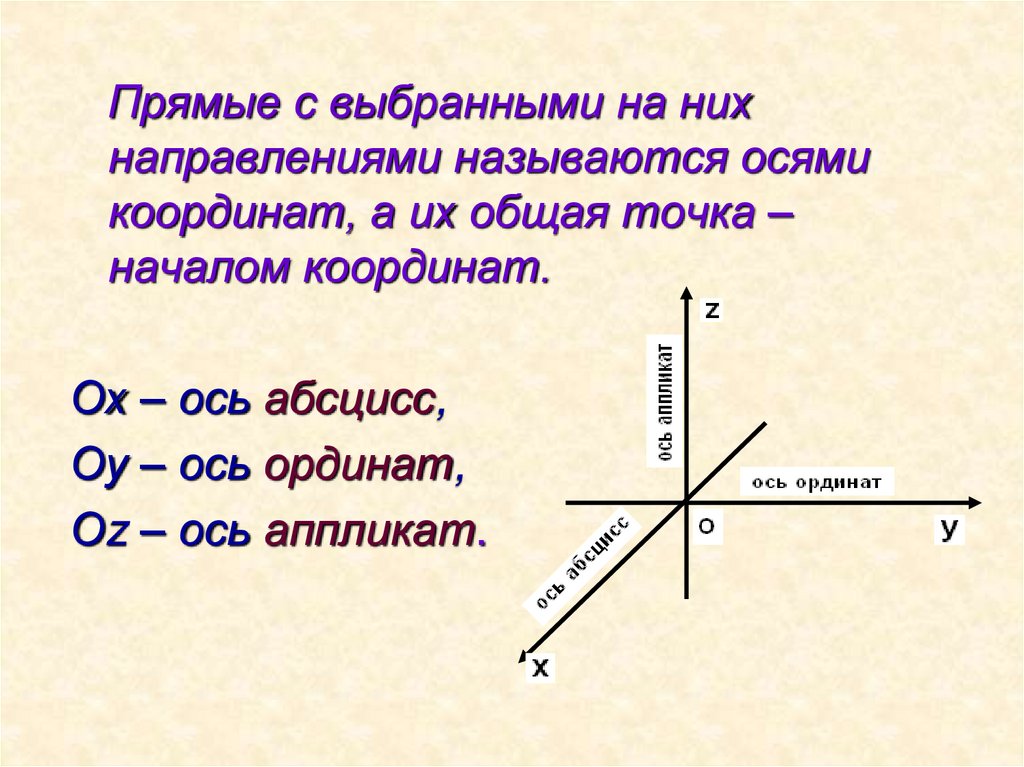
Прямые с выбранными на них
направлениями называются осями
координат, а их общая точка –
началом координат.
Ох – ось абсцисс,
Оу – ось ординат,
Оz – ось аппликат.

5.

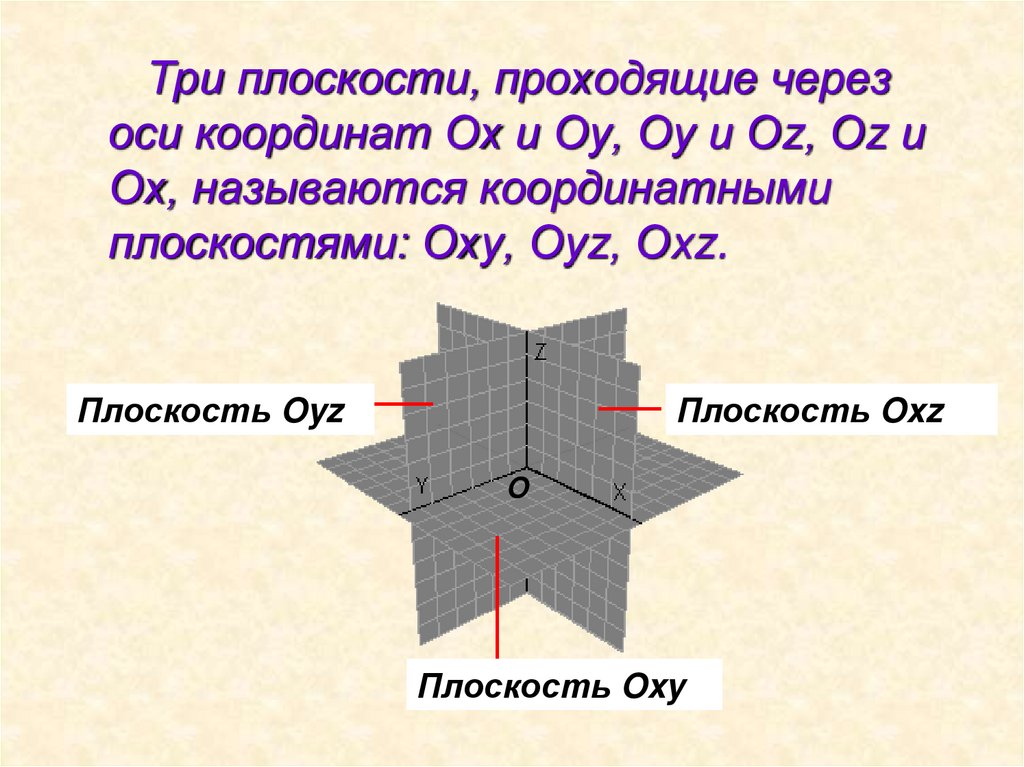
Три плоскости, проходящие через
оси координат Ох и Оу, Оу и Оz, Оz и
Ох, называются координатными
плоскостями: Оху, Оуz, Оxz.
Плоскость Oyz
Плоскость Oxz
O
Плоскость Oxy

6.

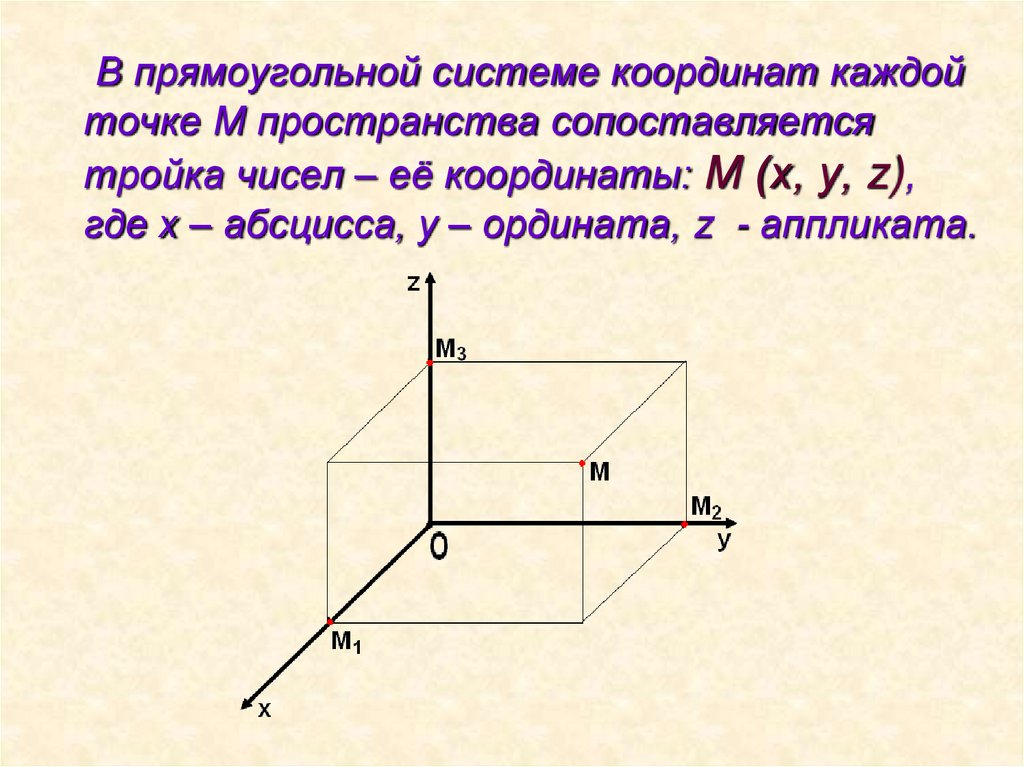
В прямоугольной системе координат каждой
точке М пространства сопоставляется
тройка чисел – её координаты: М (х, у, z),
где х – абсцисса, у – ордината, z - аппликата.

7.

Нахождение точки на координатной
плоскости.
Если, например, точка M лежит на координатной
плоскости или на оси координат, то некоторые её
координаты равны нулю. Так, если M принадлежит
Oxy, то аппликата точка M равна нулю: z=0.
Аналогично если M принадлежит Oхz, то y=0, а если M
принадлежит Oyz, то x=0. Если M принадлежит Ox, то
ордината и аппликата точки M равна нулю: y=0 и z=0.
Если M принадлежит Oy, то x=0 и z=0; если M
принадлежит Oz, то x=0 и y=0. Все три координаты
начала координат равны нулю: О (0;0;0).

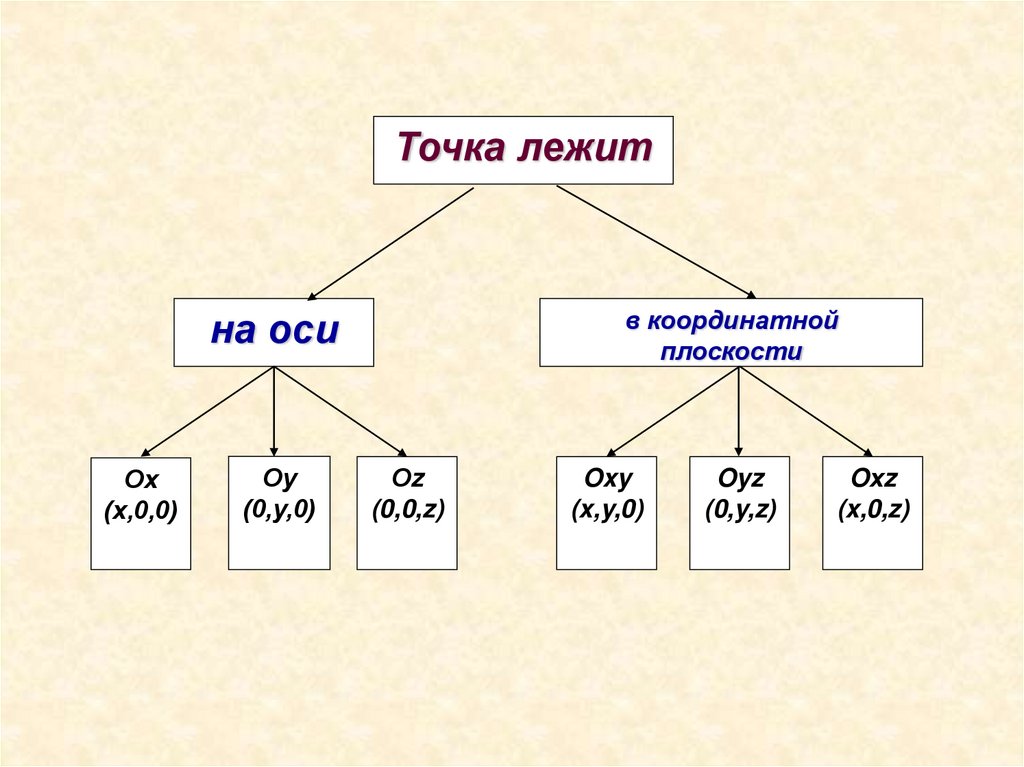
8.

Точка лежит
в координатной
плоскости
на оси
Ох
(х,0,0)
Оу
(0,у,0)
Оz
(0,0,z)
Oxy
(x,y,0)
Oyz
(0,y,z)
Oхz
(x,0,z)

9.

Вариант 1.
Построить точки
А(3;-1;0), В(0;0;-7),
С(2;0;0), D(-4;0;3),
E(0;-1;0), F(1;2;3)
Вариант 2.
Построить точки
А(-3;0;0), В(0;1;-7),
С(0;2;0), D(-2;0;3),
E(-1;0;0), F(3;2;1)