Координаты и векторы

1. Координаты и векторы

2. Прямоугольная система координат в пространстве

Если через точку пространства проведены три попарно
перпендикулярные прямые, на каждом из них выбрано
направление(оно обозначается стрелкой) и выбрана
единица измерения отрезков, то говорят, что задана
прямоугольная (декартова) система
координат в пространстве.

3.

z
Ось аппликат
Прямые с выбранными на них
направлениями называются
осями координат, а их общая
точка – началом координат.
Обозначаются Oх, Oy, Oz.
Плоскости, проходящие
соответственно через оси
координат Ох и Оy, Oу и Оz, Oz и
Ox, называются координатными
плоскостями и обозначаются Oxy,
Oхz, Ozy.
Точка О разделяет каждую из осей
координат на два луча. Луч,
направление которого совпадает
с направлением оси, называется
положительной полуосью, а
другой луч – отрицательной
полуосью.
y
O
x
Ось ординат
Система координат
Oxyz

4.

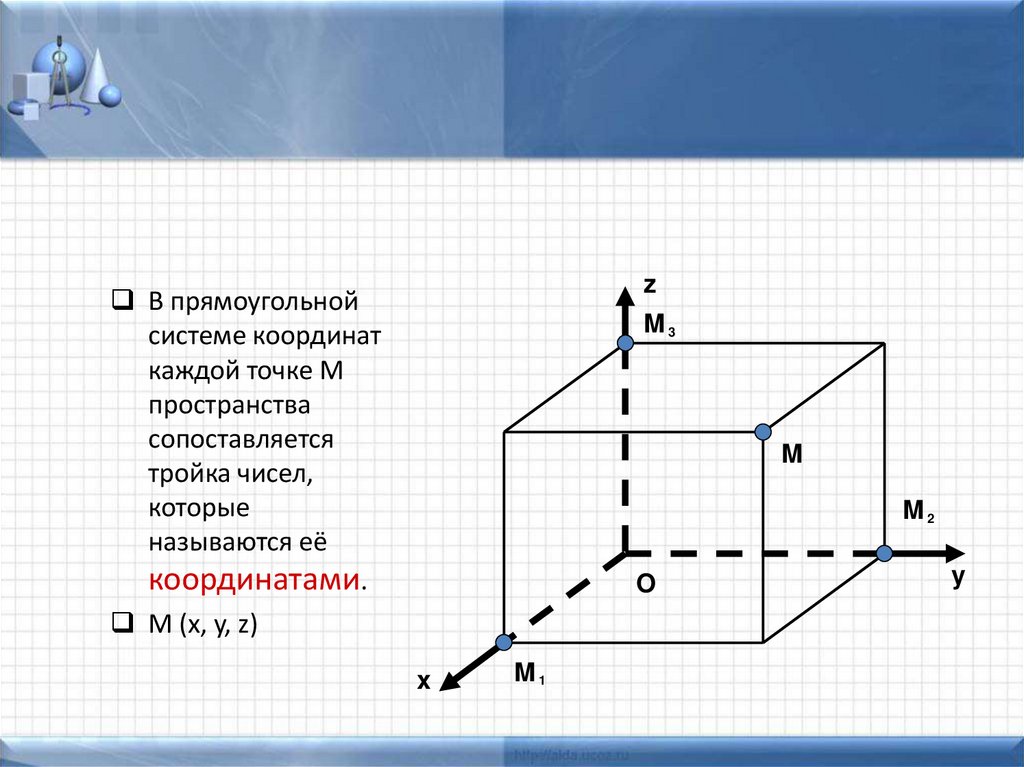
z
В прямоугольной
системе координат
каждой точке M
пространства
сопоставляется
тройка чисел,
которые
называются её
координатами.
M (x, y, z)
M3
M
M2
O
x
M1
y

5.

Координаты точки, лежащей
На оси
В координатной плоскости
Ox (x; 0; 0)
Oxy (x; y; 0)
z
Oy (0; y; 0)
O
x
Oz (0; 0; z)
Oyz
(0; y; z)
y
Oxz (x; 0; z)

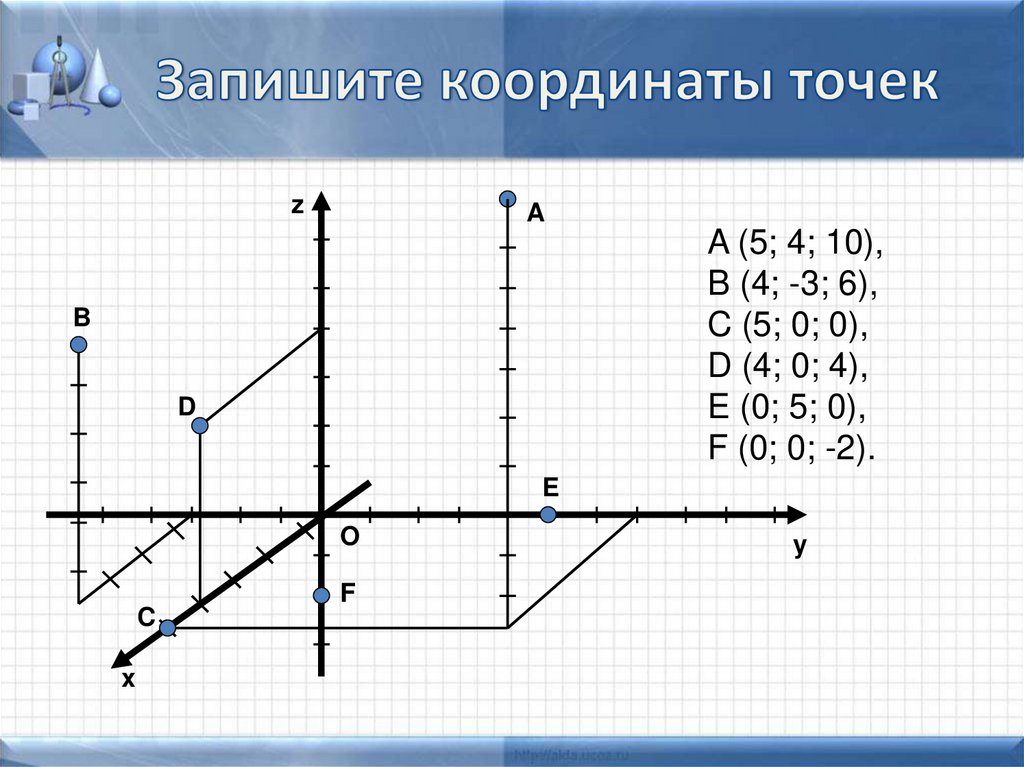
6. Запишите координаты точек

z
A
A (5; 4; 10),
B (4; -3; 6),
C (5; 0; 0),
D (4; 0; 4),
E (0; 5; 0),
F (0; 0; -2).
B
D
E
O
F
C
x
y

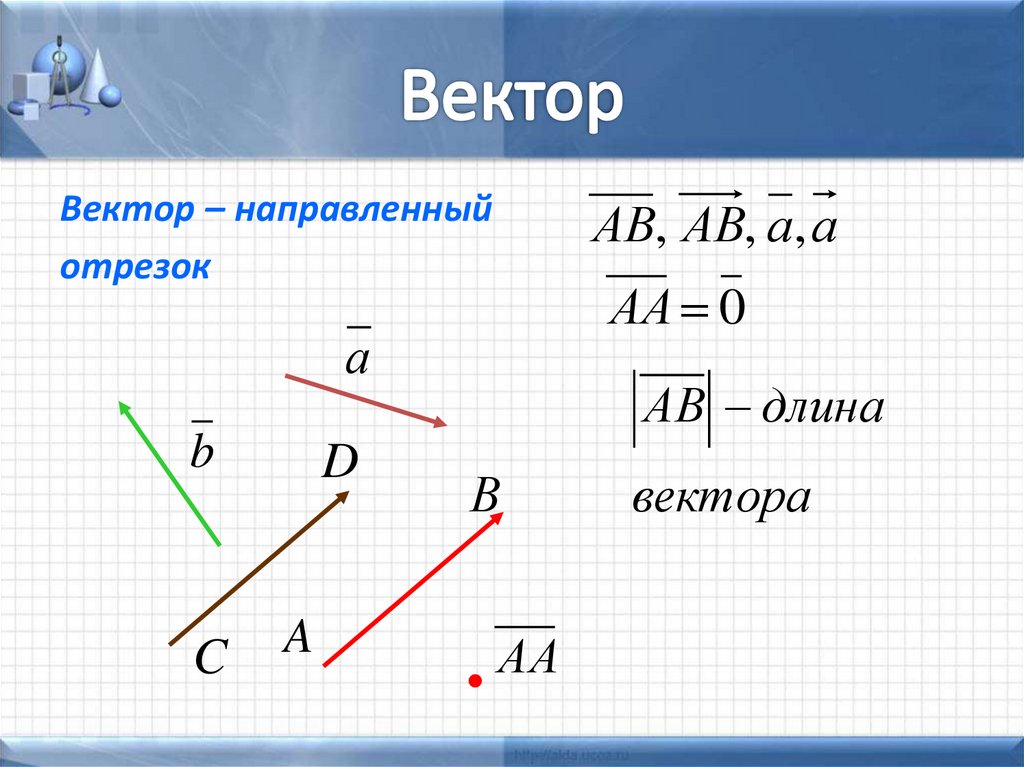
7. Вектор

– направленный
отрезок
АВ, АВ, а, а
АА 0
а
b
C
D
A
АВ длина
В
АА
вектора

8. Координаты вектора

• Координаты вектора
равны разности координат
AB( xB
его конца и начала
• Координаты вектора,
началом которого
является начало
координат (радиусвектора), равны
координатам его конца.
x A ; yB y A ; zB z A )
OA( x A ; y A ; z A )

9. Задача: Найдите координаты вектора АВ, если:

A 2; 5; 3 , B 0; 4; 9
A 3; 7;1 , B 7; 8;12

10. Абсолютная величина вектора

a
( модуль вектора,
длина вектора)
равна корню
AB
квадратному из
суммы квадратов его
координат
x y z
2
a
x
2
AB
2
a
y
0 0
2
AB
2
a
z
2
AB

11. Расстояние между точками

Расстояния между точка M (x ; y ; z ) и
M (x ; y ; z ) вычисляется по формуле
1
2
2
2
1
1
2
d = √(x – x )² + (y – y )² + (z – z )²
2
1
2
1
2
1
1

12. Задача: Найдите абсолютную величину вектора:

1. Каждая координата суммы двух или более
векторов равна сумме соответствующих
координат этих векторов.
a {x1;y1;z1}
b {x2;y2;z2}
a +b {x1+x2; y1+y2; z1+z2}

13. Правила нахождения суммы, разности и произведения на данное число.

2. Каждая координата разности двух
векторов равна разности соответствующих
координат этих векторов.
a {x1;y1;z1}
b {x2;y2;z2}
a –b {x1–x2; y1 –y2; z1– z2}

14.

3. Каждая координата произведения вектора
на число равна произведение
соответствующей координаты вектора на
это число.
a {x; y; z}
ka {kx; ky; kz}

15.

Ответ: