3.6 _Принцип Даламбера (пример)

1.

Динамика
Тема 3.6 Принцип Даламбера
Саврасова Наталья Рэмовна
Слепова Светлана Владимировна
Игнатова Анастасия Валерьевна
Доценты кафедры «Техническая механика»
1

2.

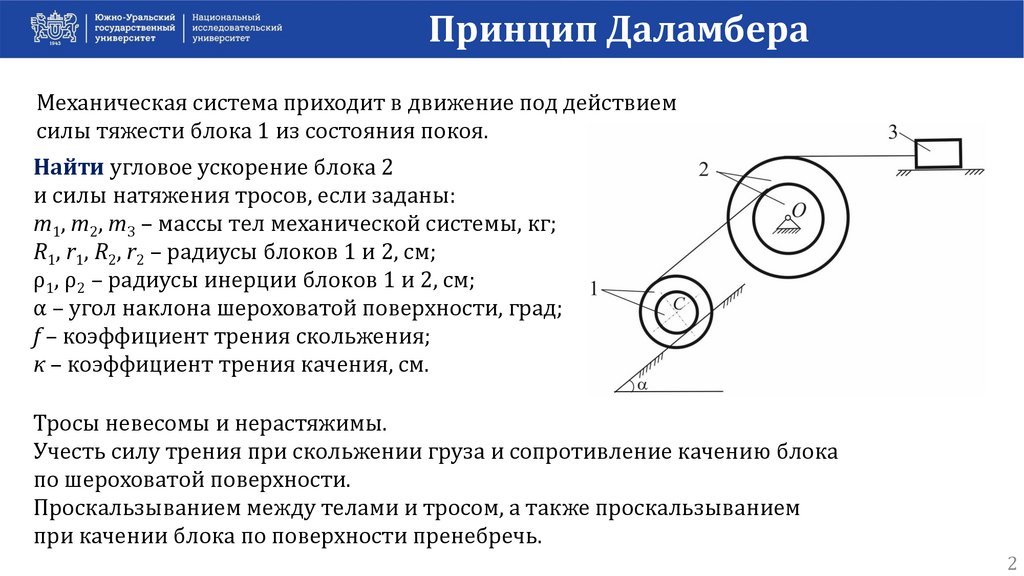
Принцип Даламбера
Механическая система приходит в движение под действием
силы тяжести блока 1 из состояния покоя.
Найти угловое ускорение блока 2
и силы натяжения тросов, если заданы:
m1, m2, m3 – массы тел механической системы, кг;
R1, r1, R2, r2 – радиусы блоков 1 и 2, см;
ρ1, ρ2 – радиусы инерции блоков 1 и 2, см;
α – угол наклона шероховатой поверхности, град;
f – коэффициент трения скольжения;
к – коэффициент трения качения, см.
Тросы невесомы и нерастяжимы.
Учесть силу трения при скольжении груза и сопротивление качению блока
по шероховатой поверхности.
Проскальзыванием между телами и тросом, а также проскальзыванием
при качении блока по поверхности пренебречь.
2

3.

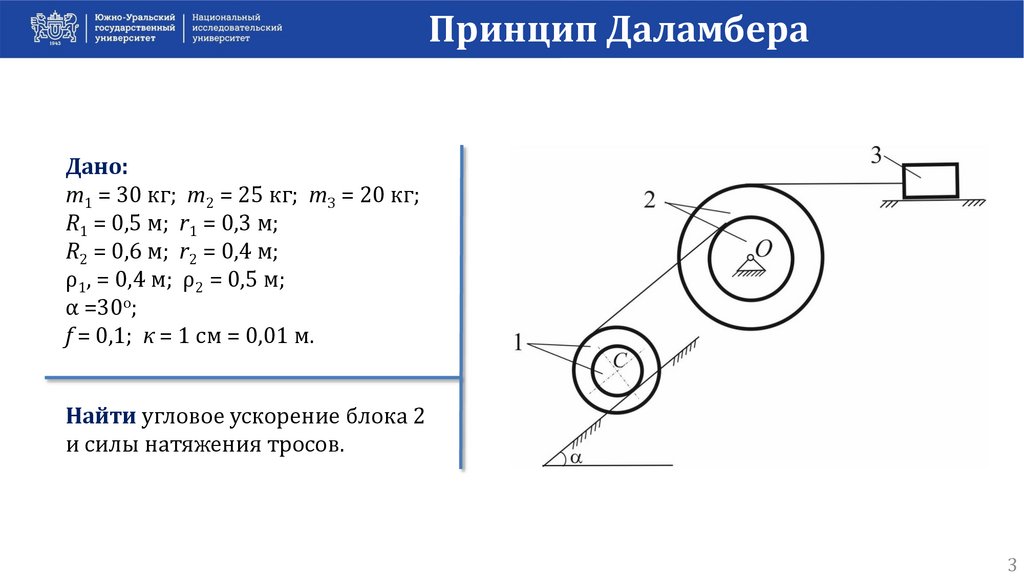
Принцип Даламбера
Дано:
m1 = 30 кг; m2 = 25 кг; m3 = 20 кг;
R1 = 0,5 м; r1 = 0,3 м;
R2 = 0,6 м; r2 = 0,4 м;
ρ1, = 0,4 м; ρ2 = 0,5 м;
α =30о;
f = 0,1; к = 1 см = 0,01 м.
Найти угловое ускорение блока 2
и силы натяжения тросов.
3

4.

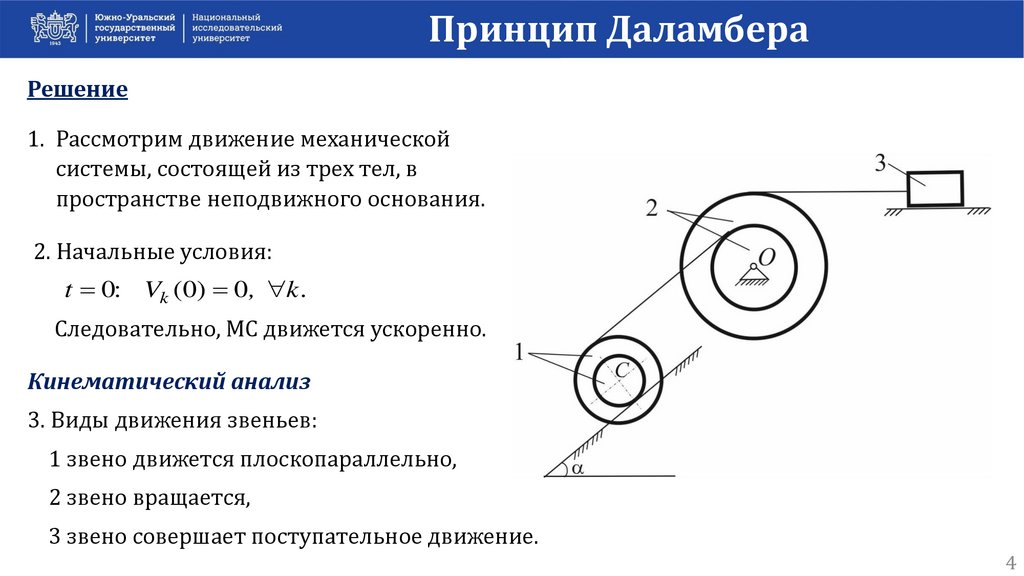
Принцип Даламбера
Решение
1. Рассмотрим движение механической
системы, состоящей из трех тел, в
пространстве неподвижного основания.
2. Начальные условия:
t 0: Vk (0) 0 , k.
Следовательно, МС движется ускоренно.
Кинематический анализ
3. Виды движения звеньев:
1 звено движется плоскопараллельно,
2 звено вращается,
3 звено совершает поступательное движение.
4

5.

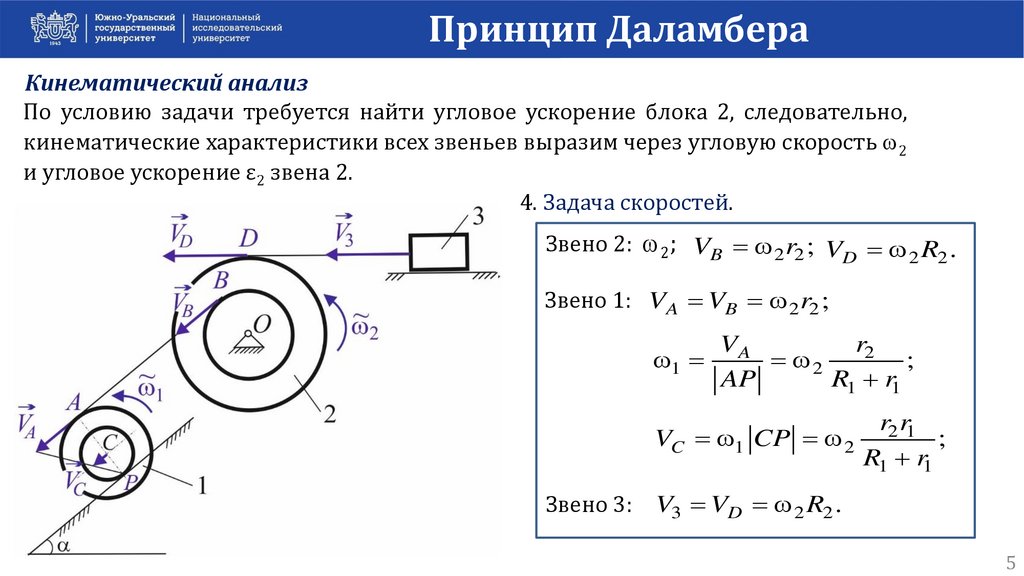
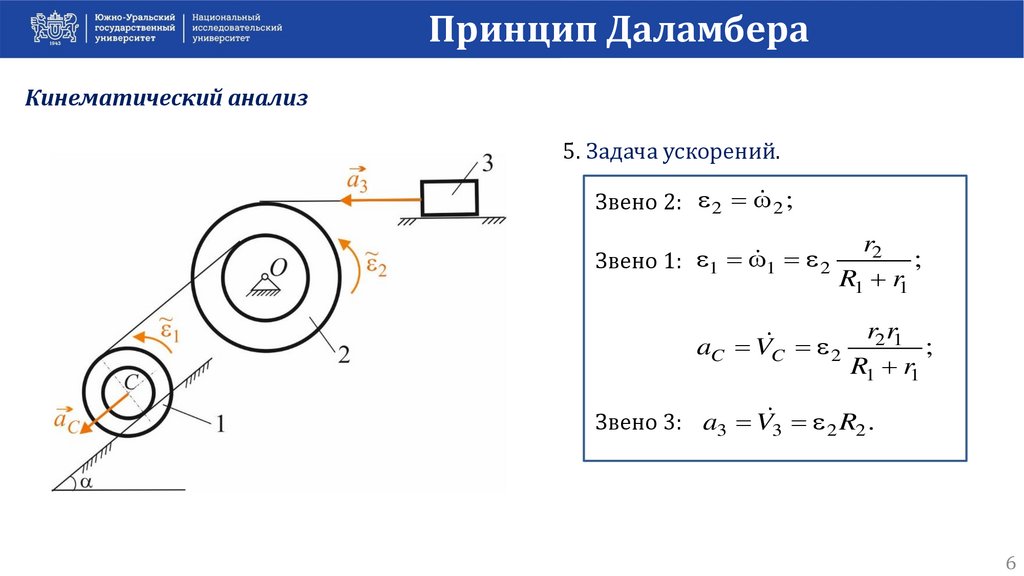
Принцип Даламбера
Кинематический анализ
По условию задачи требуется найти угловое ускорение блока 2, следовательно,
кинематические характеристики всех звеньев выразим через угловую скорость 2
и угловое ускорение ε2 звена 2.
4. Задача скоростей.
Звено 2: 2; VB 2 r2 ; V R .
D
2 2
Звено 1: VA VB 2 r2 ;
VA
r2
1
2
;
AP
R1 r1
r2 r1
VC 1 CP 2
;
R1 r1
Звено 3: V3 VD 2 R2 .
5

6.

Принцип Даламбера
Кинематический анализ
5. Задача ускорений.
Звено 2: 2 2 ;
r2
;
Звено 1: 1 1 2
R1 r1
r2 r1
aC VC 2
;
R1 r1
Звено 3: a3 V3 2 R2 .
6

7.

Принцип Даламбера
Динамический анализ
Механическую систему разобьем на отдельные тела
и рассмотрим движение каждого из тел.
I
1. Рассмотрим плоскопараллельное движение блока 1 в ИСО.
2. Активные силы: m1g
3. Связи:
(3-0) – шероховатая поверхность,
(3-2) – гибкая невесомая нерастяжимая нить.
Заменим связи реакциями: N1 , Fтр1 , M тр.кач. , R21 .
7

8.

Принцип Даламбера
4. Для решения задачи применяем принцип Даламбера:
F a , R,
dФ ~ 0
При движении МС в любой момент времени
приложенные к каждой точке системы активные
силы, реакции связей вместе с силами инерции
образуют систему сил, эквивалентную нулю.
5. Систему приложенных к точкам тела сил инерции
приводим к центру масс С:
dФ ~ Ф1 m1aC , M CФ IC z 1
1
r2 r1
Ф1 m1 aC1 m1 2
,
R1 r1
6. Система сил:
1
M CФ1
1
I C1z 1 m1 12 2
r2
.
R1 r1
m1 g , N1 , Fтр1 , M тр.кач. , R21 , Ф1 , M CФ ~ 0 – плоская произвольная.
8

9.

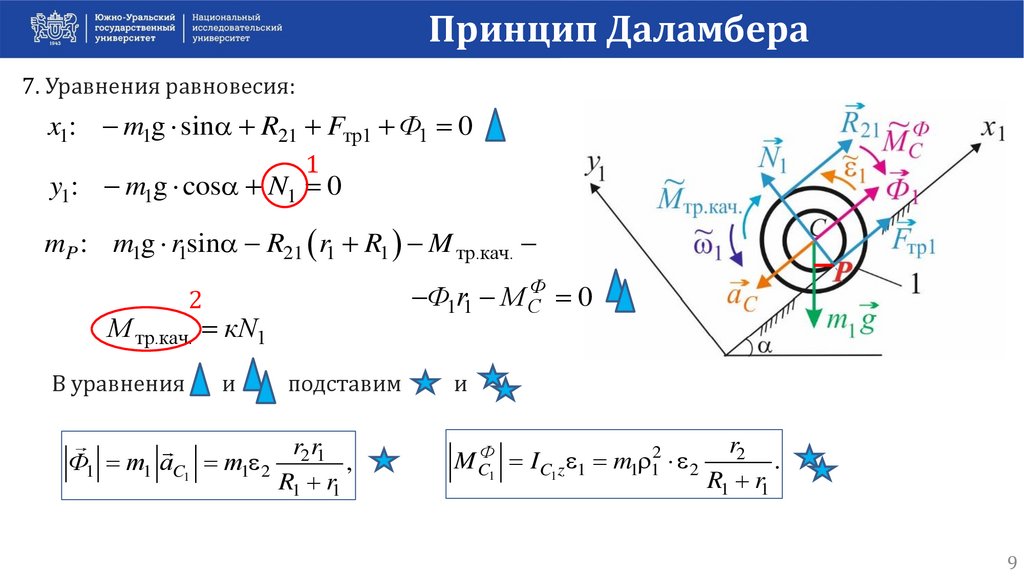
Принцип Даламбера
7. Уравнения равновесия:
x1: m1g sin R21 Fтр1 Ф1 0
1
y1: m1g cos N1 0
mP : m1g r1sin R21 r1 R1 M тр.кач.
Ф1r1 M СФ 0
2
М тр.кач. кN1
В уравнения
и
подставим
r2 r1
Ф1 m1 aC1 m1 2
,
R1 r1
и
M CФ1 I C1z 1 m1 12 2
r2
.
R1 r1
9

10.

Принцип Даламбера
7. Уравнения равновесия:
x1: m1g sin R21 Fтр1 Ф1 0
y1: m1g cos N1 0
mP : m1g r1sin R21 r1 R1 M тр.кач.
М тр.кач. кN1
Уравнения
и
с учётом
Ф1r1 M СФ 0
и
принимают вид:
r2 r1
m1g sin R21 Fтр1 m1 2
0
R1 r1
(1)
r2 r12
r2
2
m1g r1sin R21 r1 R1 к m1gcos m1 2
m1 1 2
0
R1 r1
R1 r1
(2)
10

11.

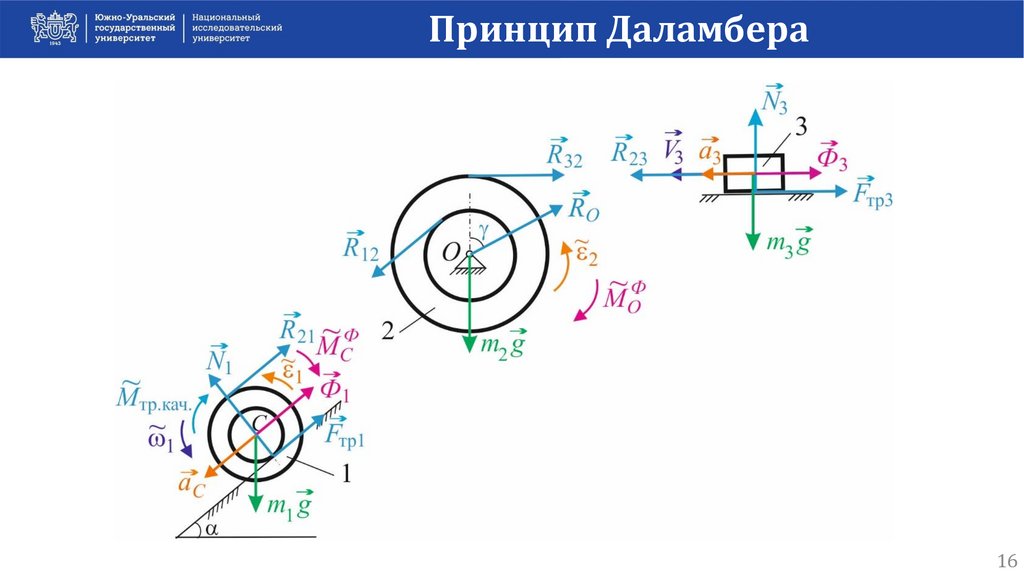
Принцип Даламбера
II 1. Рассмотрим вращательное движение блока 2 в ИСО.
2. Активные силы: m2 g
3. Связи:
(2-0) – неподвижный цилиндрический шарнир,
(2-1) – гибкая невесомая нерастяжимая нить.
(2-3) – гибкая невесомая нерастяжимая нить.
Заменим связи реакциями:
R12 , R32 , RO .
11

12.

Принцип Даламбера
4. Применяем принцип Даламбера:
F a , R,
dФ ~ 0
При движении МС в любой момент времени
приложенные к каждой точке системы активные
силы, реакции связей вместе с силами инерции
образуют систему сил, эквивалентную нулю.
5. Вводим фиктивные силы инерции:
dФ ~ Ф2 m2 aC2 , M OФ I Оz 2
0
M OФ I Oz 2 m2 22 2 .
6. Система сил:
m g , R , R , R , M ~ 0 – плоская произвольная.
2
12
32
O
Ф
O
12

13.

Принцип Даламбера
7. Уравнения равновесия:
x2 : R12cos R32 ROx 0
(3)
y2 : m2g R12sin ROy 0
(4)
mО :
R12 r2 R32 R2 M OФ 0
Уравнение
с учётом
M OФ I Oz 2 m2 22 2
принимает вид:
R12 r2 R32 R2 m2 22 2 0
(5)
13

14.

Принцип Даламбера
III 1. Рассмотрим поступательное движение груза 3 в ИСО.
2. Активные силы: m3g
3. Связи: (3-0) – шероховатая поверхность,
(3-2) – гибкая невесомая нерастяжимая нить.
Заменим связи реакциями: N 3 , Fтр3 , R23 .
4. Применяем принцип Даламбера:
F a , R,
dФ ~ 0
При движении МС в любой момент времени
приложенные к каждой точке системы активные
силы, реакции связей вместе с силами инерции
образуют систему сил, эквивалентную нулю.
14

15.

Принцип Даламбера
5. Вводим фиктивные силы инерции:
dФ ~ Ф3 m3aC , M СФ IС z 3
3
3
3
Ф3 m3 a3 m3 2 R2
0
6. Система сил:
m3 g , R23 , N3 , Fтр3 , Ф3 ~ 0 – плоская сходящаяся.
7. Уравнения равновесия:
x3: R23 Fтр3 Ф3 0
1
y3: m3g N3 0
2
Уравнение
Fтр3 f N3
с учётом
принимает вид:
R23 f m3 g m3 2 R2 0
(6)
15

16.

Принцип Даламбера
16

17.

Принцип Даламбера
r2 r1
m1g sin R21 Fтр1 m1 2
0
R1 r1
(1)
r2 r12
r2
2
m1g r1sin R21 r1 R1 к m1gcos m1 2
m1 1 2
0
R1 r1
R1 r1
R12cos R32 ROx 0
(3)
m2g R12sin ROy 0
(4)
R12 r2 R32 R2 m2 22 2 0
(5)
R23 f m3 g m3 2 R2 0
(6)
(2)
17

18.

Принцип Даламбера
m1
r2
2
2
r1 1 (7)
Из (2) R21
g r1sin кcos 2
R1 r1
r1 R1
Из (6)
R23 m3 f g 2 R2
(8)
R12 , R32 (5) R12 r2 R32 R2 m2 22 2 0
m1gr2 r1sin кcos
r1 R1
m1 2
r R
r22
1
2
2
2
2
r
f
m
gR
m
R
m
1
3
2
3 2 2
2 2 2 0
2 1
1
m1gr2 r1sin кcos
2
2
2
2
2
f m3 gR2
r
m
m
R
1
1
2 2
3 2
2
r1 R1
r1 R1
m1r22
(9)
(7) R21
(9)
(8) R23
1
(9)
18

19.

Принцип Даламбера
Вычислим:
30 9,8 0,4 0 ,3sin30о 0 ,01cos30о
0 ,1 20 9 ,8 0 ,6
0,3 0,5
0 ,59 рад/c 2
2
30 0 ,42
0 ,32 0 ,42 25 0 ,52 20 0 ,62
0 ,3 0 ,5 2
30
0 ,59 0 ,4
о
о
2
2
R21
0 ,3 0 ,4 49 ,18 Н
9,8 0 ,3sin30 0 ,01cos30
0 ,3 0 ,5
0,3 0,5
R23 20 0 ,1 9 ,8 0 ,59 0 ,6 26 ,68 H
Ответ:
2 0 ,59 рад/c 2 ;
R21 49 ,18 Н;
R23 26 ,68 H.
Задача решена
19

20.

Принцип Даламбера
Жан Леро́ н Д’Аламбе́ р (Даламбер)
16.11.1717 – 29.10.1783
Французский учёный-энциклопедист.
Широко известен как философ, математик и
механик. Член Парижской академии наук (1740),
Французской Академии (1754), Петербургской
(1764) и других академий.
Наше занятие закончено.
Спасибо за внимание!
20