Задача силового анализа действующих на механизм

1.

КИНЕТОСТАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ
Задача силового анализа
действующих на механизм.
механизма
–
определение
сил,
Машинный агрегат можно представить в виде схемы:
Механизмы
двигателя
Передаточные
механизмы
Технологич. машины
механизма
На данной части машинного агрегата действуют:
1) движущие силы, которые стремятся ускорить движение
механизма, совершающие полезную работу (в двигателе внутреннего
сгорания (ДВС) сила давления газа на такте расширения);
2) силы полезного сопротивления – те, которые необходимо
преодолеть для выполнения требуемого технологического процесса (в
станках – сила резания, в автомобилях – сила сопротивления качения);
3) силы вредных сопротивлений, на которые затрачивается
дополнительная работа сверх той, которая необходима для преодоления
сил полезного сопротивления (силы трения в узлах машины).

2.

Определение уравновешивающей силы методом построения
планов сил
Всякий механизм,
обладающий одной степенью подвижности и
находящийся под действием заданной системы внешних сил, можно
считать находящимся в равновесии, если к одному из его звеньев
приложить уравновешивающее эту систему усилие.
Уравновешивающим силовым фактором может быть либо некоторая
условная уравновешивающая сила Ру, либо уравновешивающая пара сил
с моментом Му.
Последовательность силового анализа механизма:
1. Произвести структурный анализ механизма.
2. Произвести кинематический анализ.
3. Найти силы тяжести, силы инерции, момент от пар сил инерции, силу
давления газов.
4. К наиболее удаленной от механизма первого класса группе Ассура
приложить найденные силы и реакции.
5. Найти реакции с помощью многоугольника сил.
6. Произвести анализ механизма первого класса, найти реакции,
уравновешивающую силу и уравновешивающий момент.

3.

Задачей силового анализа механизма является определение сил,
действующих на звенья механизма, реакций в кинематических парах и
уравновешивающих сил (уравновешивающих моментов). Полученные
при анализе силы являются исходными для расчета на прочность и
износ деталей и узлов механизма, при подборе мощности привода,
расчете механического КПД.
Для определения реакций в кинематических парах удобно
пользоваться принципом Даламбера, который можно сформулировать
так: «Можно отдельно рассматривать часть механизма, как будто она
продолжает находиться в работающем или покоящемся механизме, в
том случае, если приложить к ней все действующие силы, а в
«разорванные» кинематические пары реакции».
Если часть механизма рассматривается без нарушения ее движения
или покоя, то для нее верны уравнения статики:
где:
M
i
0
F 0
i
Fi
- силы, действующие на часть механизма, включая реакции;
Мi
- моменты сил, относительно какой либо точки.

4.

Находить неизвестные реакции в кинематических парах, можно
пользуясь уравнениями статики, поэтому такой силовой анализ
называется кинетостатическим.
При
кинетостатическом
анализе
механизм
рассматривается
последовательно по частям. Этими частями являются группы Ассура и
механизм первого класса. Это удобно ввиду того, что число уравнений
статики для группы Ассура равно числу неизвестных реакций, которые
в таком случае легко находятся.
Кинетостатический анализ в первом приближении производится без
учета сил трения в кинематических парах, ввиду их малости.

5.

Определим реакции в кинематический парах R12;R23;R01;R03 и
уравновешивающий момент для механизма двигателя Му. Известными
величинами являются: масса m3 поршня 3, диаметр d цилиндра, масса
m2, длина lВА и момент инерции J2 шатуна 2, длина кривошипа lОА,
давление в цилиндре рiВ, а также постоянная угловая скорость 1
кривошипа 1. Центры масс звеньев 1, 2, 3 лежат соответственно в
точках О, S2, В.
Силы тяжести звеньев 2 и 3 определяются по формулам:
G2 = m2 g, G3 = m3 g,
где g=9,8 м/с^2 - ускорения свободного падения.
Силы тяжести звеньев направляются вертикально вниз.
Силы инерции звеньев 2 и 3 определяются по формулам:
Fи2 = m2 aS2 , Fи3 = m3 ab,
где: aS2, ab, - ускорения центров масс звеньев 2 и 3, определенные в
ходе кинематического анализа.
Силы
инерции
звеньев
направляются
противоположно
соответствующим ускорениям.

6.

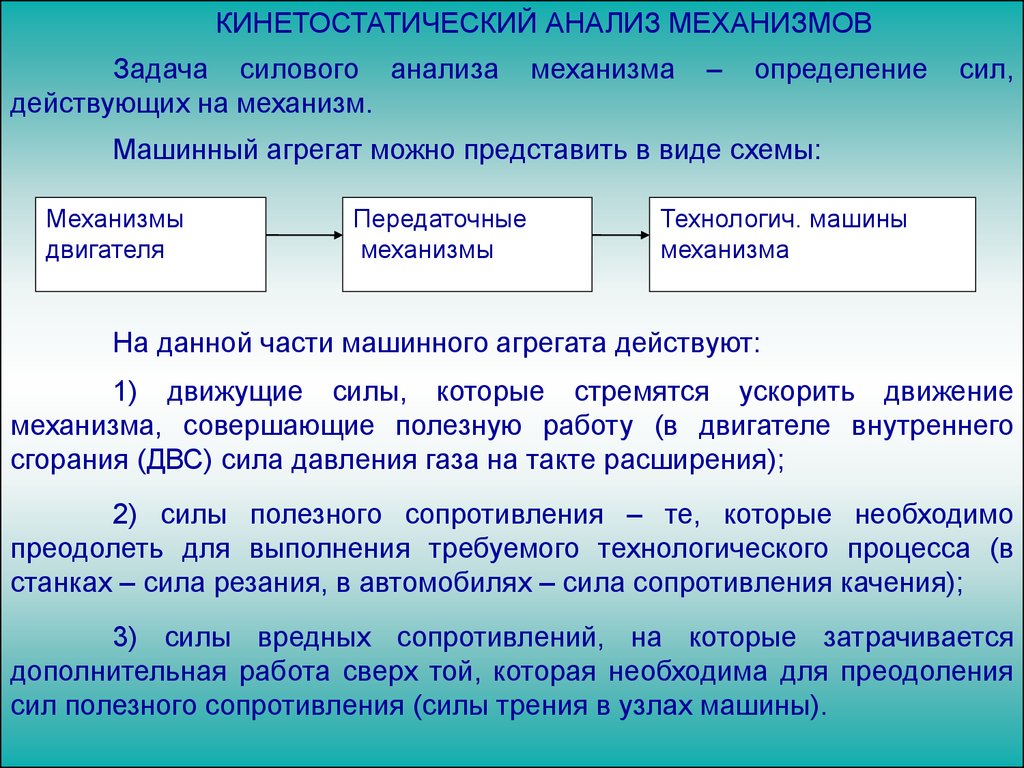
Произведем силовой анализ кривошипно-ползунного механизма двигателя
внутреннего сгорания для заданного положения.
Определение сил тяжести звеньев
В
3
Силы тяжести шатуна 2 и поршня 3
определяются по формулам:
2
S2
А
G2 m2 g, H ;
ω1
1
G3 m3 g , H ,
О
где g - ускорение свободного падения g = 9,8
м / с2.

7.

Площадь поперечного сечения цилиндра
FB
d2
4
, м2.
Сила давления газов на поршень В
PДB PiB FB , Н .
Определение результирующих сил инерции
Сила инерции шатуна 2 определятся по формуле
Ри 2 m2 aS 2 , Н .
Сила инерции поршня 3 определятся
Силы инерции звеньев
направляются
противоположно
соответствующим ускорениям.
P и 3 m3 a B , Н .
Момент пар сил инерции шатуна 2 определятся по формуле
M и 2 J S 2 2 , Н м,
Момент инерции направляется
противоположно
соответствующему угловому
ускорению.
Угловое ускорение определятся по формуле
a BA 2
2
,c .
l AB
Момент удобно представить в виде пары сил, приложенных в
точках А и В шатуна 2, перпендикулярно ему.
Pми2 M и 2 / l AB , H .

8.

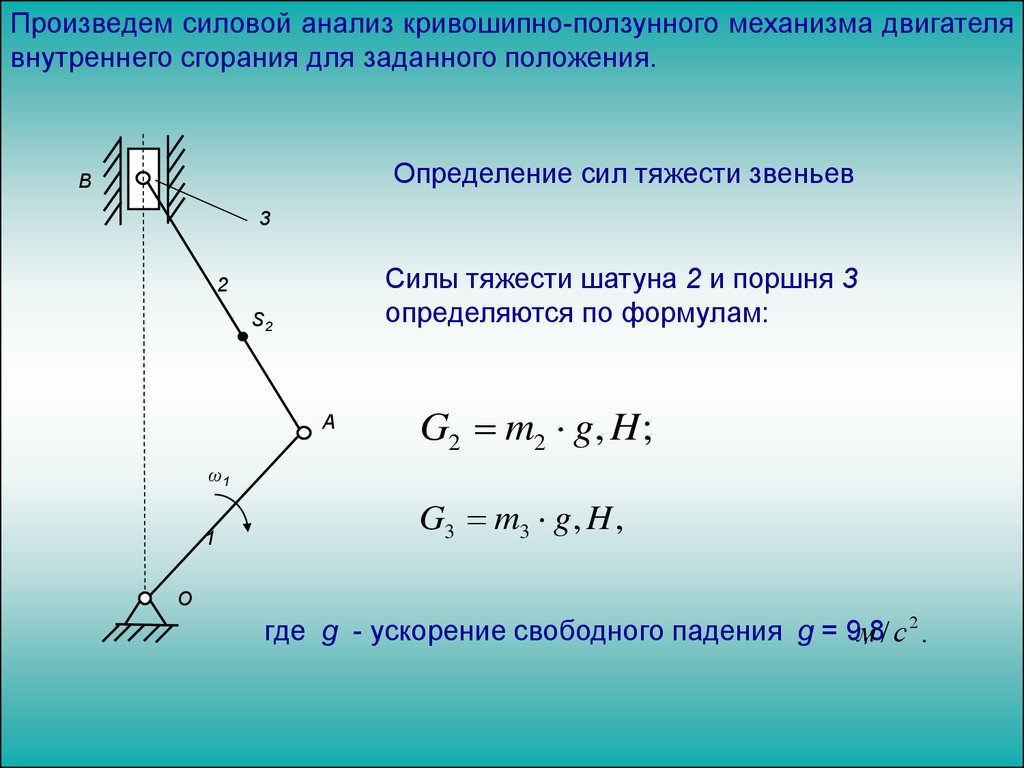
Определение силы давления газов на поршень
Такты:
1.Всасывание горючей смеси
(0º -180º).
2.Сжатие (180º-360º).
3.Рабочий ход (360º-540º).
4.Выхлоп (540º-720º).
Теоретическая (пунктир) и действительная
(сплошные линии) индикаторные диаграммы 4—
тактного двигателя: ra — линия впуска; ac — линия
сжатия; cz — линия сгорания; zb — линия
расширения; br — линия выпуска; P давление; V —
объём

9.

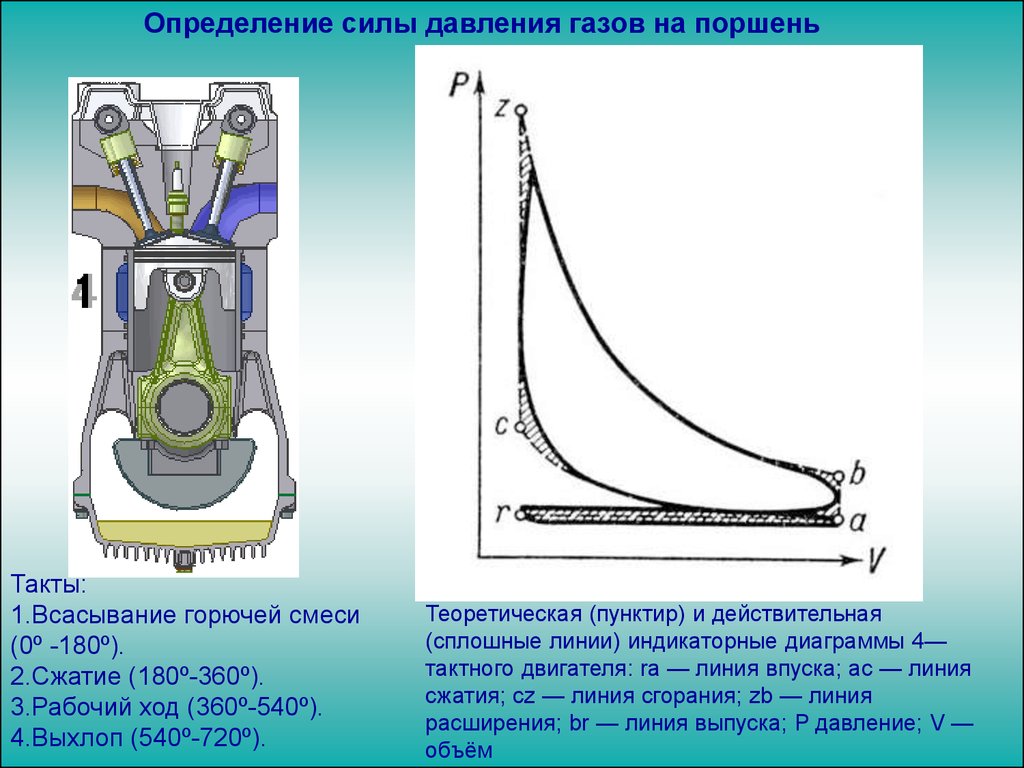
Силовой анализ группы Ассура 2-3
принцип Даламбера:
систему можно рассматривать без нарушения движения
или покоя, если при отсоединении от механизма
приложить к ней все силы, включая силы инерции и
силы реакции в разрушенных шарнирах.
Ри3
R03
В
Рми2
n
R12 R12 R12
hP
П
G3
Рдв
Pи2
Мми2
aА
S2
аs2
а
hG
Рми2
G2
Rτ12
S2
аnВА
А
аВ
в
аτВА
n2
Rn12
n
P ДB Pи 2 Pи 3 G 2 G3 R12 R12 R03 P ми2 P ми2 0.
M P P
B
R12
и2
l
l AB
h1 G2 h2 R12
l AB / l Pми2 l AB / l 0.
Pи 2 h1 G2 h2 Pми2 l AB / l , H .

10.

Построение многоугольника сил
Выбирается масштабный коэффициент для построения: F Fmax
где Fmax – величина наибольшей силы;
f - длина отрезка, который будет изображать силу на плане сил.
/f
Для определения длин векторов, величины сил делят на F.
Силовой многоугольник строится в соответствии с условием Fi 0 , поэтому он
должен быть замкнутым. Вначале в любом порядке откладываются известные по
направлению и величине векторы, затем многоугольник замыкается линиями
n
действия неизвестных векторов R12
и R03, которые при пересечении ограничивают
друг друга по длине.
n
Направления R12
и R03 указывают так, чтобы многоугольник можно было «обойти»
в одну сторону по направлению стрелок. Силы Pми2 можно не учитывать,
поскольку при построении они уравновешивают друг друга.
Геометрическим сложением векторов
вектор R12.
иR12 на силовом
многоугольнике получают
R
n
12

11.

P ,
Ри3
R03
Рми2
Н
мм
G2
Ри2
G3
В
hP
РДВ
G3
Ри3
Рдв
R03
Pи2
R12
Мми2
S2
Rn12
hG
Рми2
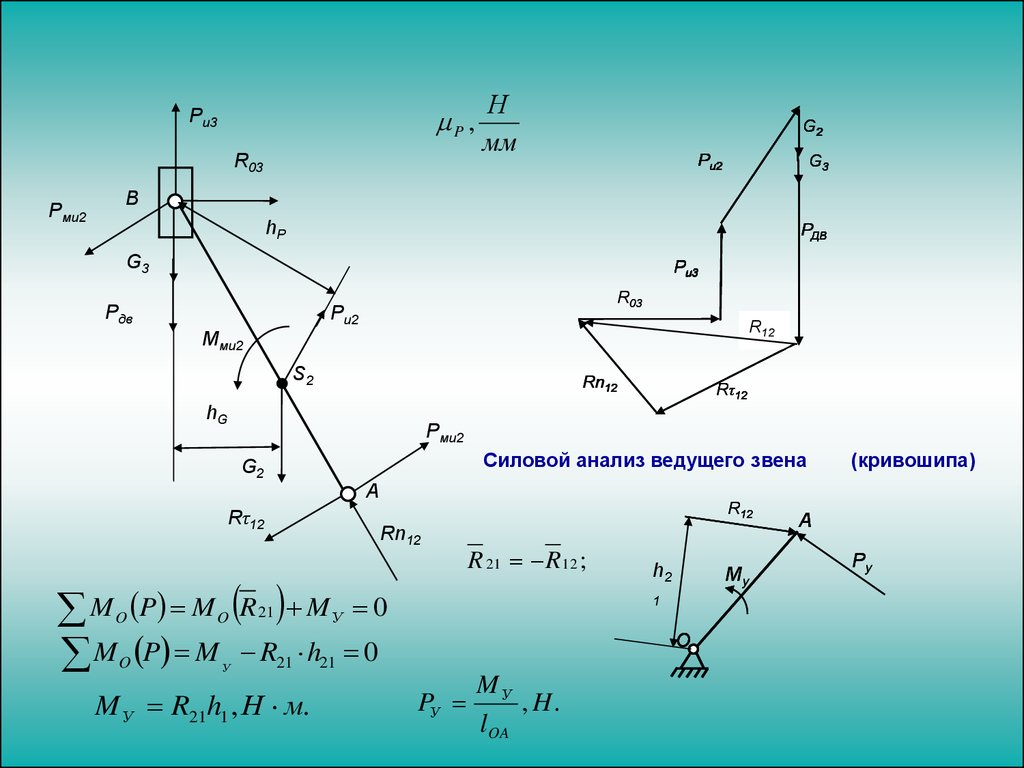
Силовой анализ ведущего звена
G2
А
Rτ12
O
O
У
R12
Rn12
M P M R M
M P M R h
O
Rτ12
21
21
M У R21h1 , Н м.
У
R 21 R 12 ;
0
Му
h2
1
О
21 0
PУ
MУ
, H.
lOA
(кривошипа)
A
Ру

12.

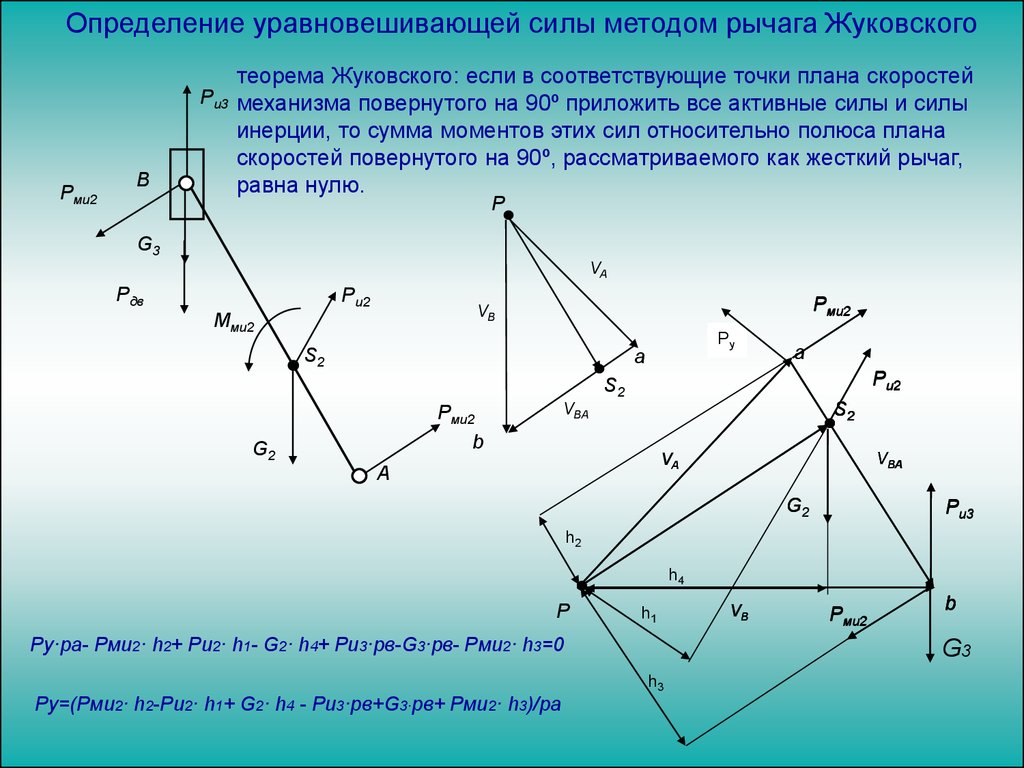
Определение уравновешивающей силы методом рычага Жуковского
Ри3
Рми2
В
теорема Жуковского: если в соответствующие точки плана скоростей
механизма повернутого на 90º приложить все активные силы и силы
инерции, то сумма моментов этих сил относительно полюса плана
скоростей повернутого на 90º, рассматриваемого как жесткий рычаг,
равна нулю.
Р
G3
VA
Рдв
Pи2
Мми2
Рми2
VВ
S2
Ру
a
a
Pи2
S2
G2
Рми2
b
S2
VВА
VВА
VA
А
Ри3
G2
h2
h4
Р
h1
Ру·ра- Рми2· h2+ Pи2· h1- G2· h4+ Ри3·рв-G3·рв- Рми2· h3=0
Ру=(Рми2· h2-Pи2· h1+ G2· h4 - Ри3·рв+G3·рв+ Рми2· h3)/ра
VВ
Рми2
b
G3
h3