ORT_lk_6_silovoy_analiz_ploskikh_mekhanizmov

1.

СИЛОВОЙ АНАЛИЗ РЫЧАЖНЫХ МЕХАНИЗМОВ
Задачи:
- определить усилия в кинематических парах механизма;
- определить величину уравновешивающей силы (или момента).
Это необходимо для:
- расчёта звеньев механизма и элементов привода на прочность, устойчивость
и пр.;
- выбора типа и расчёта мощности привода;
- прогнозирования износа трущихся поверхностей;
- выбора типа подшипников и способа их смазки;
- расчёта к.п.д. механизма и решения большого числа других более мелких
вопросов конструирования механизма.
Механизмы бывают:
- Тихоходные – в которых силы инерции намного меньше, внешних сил и ими
можно пренебречь (проводится статический расчёт;
- Быстроходные – силы инерции больше некоторых внешних сил, которыми
в этом случае можно пренебречь (например, весом деталей).
Обычно силовой анализ выполняется с использованием принципа
Д'Аламбера. В этом случае такой расчёт (анализ) часто в литературе называют
кинетостатическим.

2.

Существует несколько видов (этапов, стадий) силового анализа механизма:
А) Силовой анализ на начальном этапе.
На этом этапе для выполнения полезных функций создаётся кинематическая
схема механизма и на основании статистических данных выбираются некоторые
параметры звеньев и параметры работы его.
На этом этапе обычно предполагается, что начальное (ведущее) звено
механизма перемещается с постоянной скоростью 1 const . Это
предположение приводит к тому, что определяются несколько усреднённые
значения усилий в звеньях и кинематических парах. Но эти данные очень важны
для предварительной конструкторской проработки механизма: конструирования
звеньев механизма и кинематических пар; более точного определения весовых
и инерционных параметров звеньев; выполнения прочностных и иных расчётов
звеньев; выбора коэффициентов запаса прочности и т.д.
Б) Силовой анализ после предварительной конструкторской проработки.
Определённые новые значения параметров кинематической схемы
механизма учитываются при повторном кинематическом и силовом анализах
механизма, после чего, при необходимости, вносятся корректировки в
конструкцию механизма.
В) Силовой анализ после конструкторской разработки механизма.
На этом этапе по определённым правилам массы и моменты инерции всех
звеньев механизма приводятся к начальному звену, все внешние силы и
моменты также приводятся к начальному звену.

3.

Составляется дифференциальное уравнение движения начального звена
(динамическая модель механизма), дважды интегрируя которое определяют
закон движения ведущего звена 1 var
Иногда на этом же этапе определяют параметры маховика, производят, если
это необходимо, уравновешивание некоторых звеньев. Затем вновь
производится кинематический и силовой анализ механизма и, при
необходимости, вносятся корректировки в конструкцию механизма.
Г) Если механизм предназначен для работы на борту летательного аппарата
или в условиях космоса, когда имеют место очень жёсткие ограничения на
габаритные размеры и массу, то задаются минимальные коэффициенты запаса
прочности и некоторые из рассмотренных этапов могут повторяться
многократно.
3.1 ПОРЯДОК ВЫПОЛНЕНИЯ СИЛОВОГО АНАЛИЗА
РЫЧАЖНОГО МЕХАНИЗМА
1) Определить весовые и инерционные параметры всех звеньев механизма.
2) Оценить рабочие нагрузки, действующие на механизм.
3) Начиная с последней группы Асура произвести силовой анализ групп в
направлении начального звена методом силовых многоугольников.
4) Выполнить силовой анализ начального звена и определить
уравновешивающую силу.
5) Построить «рычаг Жуковского» и произвести расчёт уравновешивающей
силы.
6) Сравнить значения уравновешивающей силы, найденные двумя методами.

4.

3.2 СИЛЫ, ДЕЙСТВУЮЩИЕ НА МЕХАНИЗМ
Основными силами, определяющими характер движения механизма, являются
движущие силы, совершающие положительную работу, и силы полезного
(производственного) сопротивления, возникающие в процессе выполнения
механизмом полезной работы и совершающие отрицательную работу.
К движущим силам относятся: сила давления рабочей смеси на поршень
цилиндра двигателя внутреннего сгорания; момент, развиваемый
электродвигателем на ведущем валу насоса или компрессора, и т. д.
Силы полезного сопротивления — это те силы, для преодоления которых
предназначен механизм (силы сопротивления резанию в токарном станке,
сопротивления ткани проколу иглы в швейной машине и т. д.) Эти силы обычно
задаются в виде так называемых механических характеристик.
Механической характеристикой двигателя или рабочей машины
называют зависимость момента, приложенного к ведомому валу двигателя или к
ведущему валу рабочей машины, от одного или нескольких кинематических
параметров.
При работе механизма в результате действия всех приложенных к его звеньям
указанных сил в кинематических парах возникают реакции, которые
непосредственно не влияют на характер движения механизма, но на
поверхностях элементов кинематических пар вызывают силы трения. Эти силы
являются силами вредного сопротивления.

5.

Основная задача кинетостатического анализа (расчета) состоит в
определении реакций в кинематических парах механизмов или, иначе говоря,
давлений, возникающих в местах соприкосновения элементов кинематических
пар, а также в определении уравновешивающих моментов или
уравновешивающих сил.
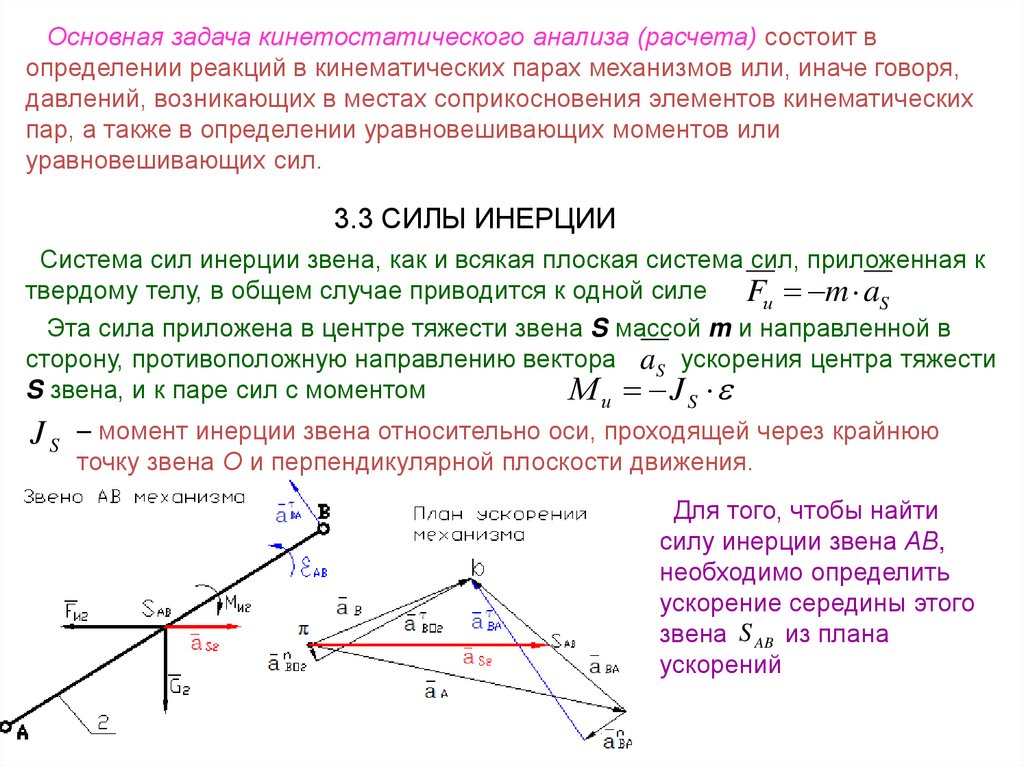
3.3 СИЛЫ ИНЕРЦИИ
Система сил инерции звена, как и всякая плоская система сил, приложенная к
твердому телу, в общем случае приводится к одной силе
Fи m aS
Эта сила приложена в центре тяжести звена S массой m и направленной в
сторону, противоположную направлению вектора aS ускорения центра тяжести
S звена, и к паре сил с моментом
М и J S
J S – момент инерции звена относительно оси, проходящей через крайнюю
точку звена О и перпендикулярной плоскости движения.
Для того, чтобы найти
силу инерции звена АВ,
необходимо определить
ускорение середины этого
звена S AB из плана
ускорений

6.

При силовом расчете механизм расчленяется на отдельные группы Асура; при
этом силовой расчет начинается с группы, присоединенной последней в
процессе образования механизма, и заканчивается расчетом ведущего
(начального) звена механизма. Если плоский механизм имеет одну степень
свободы, то начальный механизм состоит из двух звеньев: неподвижного
(стойка) и начального звена. Эти звенья образуют либо вращательную
кинематическую пару (кривошип — стойка), либо поступательную
кинематическую пару (ползун — направляющие).
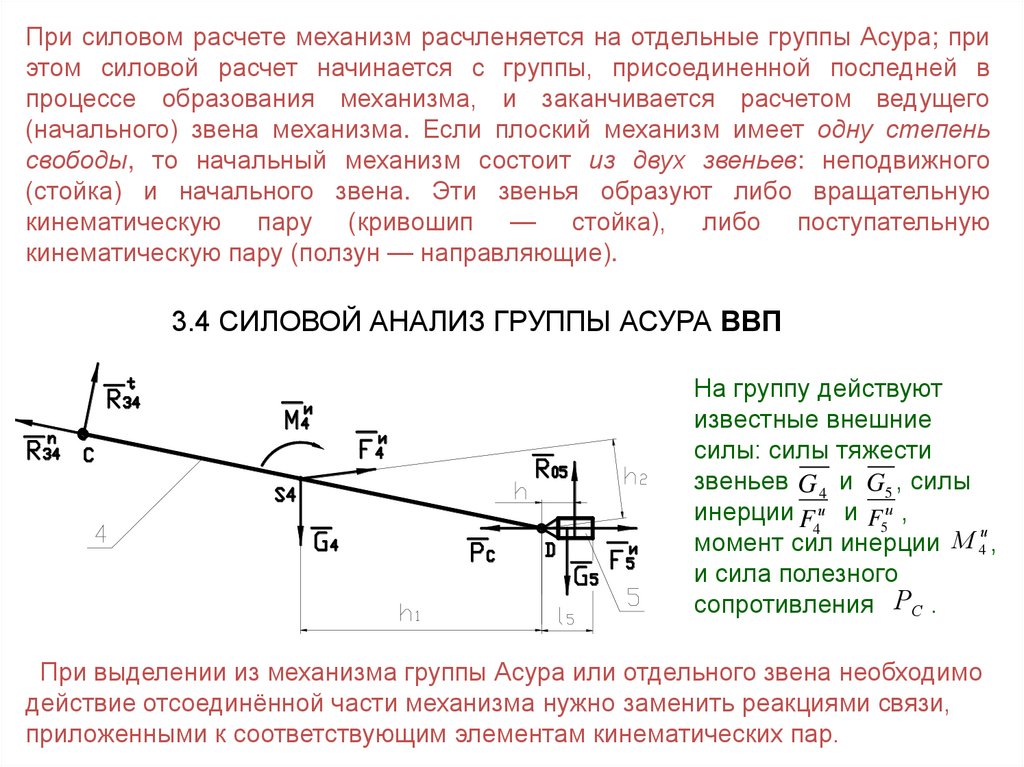
3.4 СИЛОВОЙ АНАЛИЗ ГРУППЫ АСУРА ВВП
На группу действуют
известные внешние
силы: силы тяжести
звеньев G 4 и G5 , силы
инерции F и и F5и ,
4
и
момент сил инерции М 4 ,
и сила полезного
сопротивления РС .
При выделении из механизма группы Асура или отдельного звена необходимо
действие отсоединённой части механизма нужно заменить реакциями связи,
приложенными к соответствующим элементам кинематических пар.

7.

Прикладываем неизвестные реакции R34 и R05 и составляем систему
уравнений равновесия исследуемой группы Асура:
F R R G F Р G F R 0
и
и
М
(
F
)
G
h
F
h
R
l
M
i
D ( зв4) 4 1 4 2 34 CD 4 0
l
М
(
F
)
R
h
G
0
2
F F G Р R R 0
i ( 4 5)
D
i ( зв 5 )
n
34
34
и
4
4
С
5
i ( зв 5 )
05
и
5
5
5
С
05
45
5
и
5
05
(1)
(2)
(3)
(4)
R34
можно получить из
уравнения равновесия (2)
составленного для звена 4
относительно шарнира D.
Уравнение (1) можно решить
графически методом
построения плана сил.

8.

Из уравнения (3) найдём точку приложения реакции R 05 находящейся на
расстоянии h от шарнира D:
G5 l5
h
R05 2
Для определения реакции R 45 звена
4 на звено 5 воспользуемся
уравнением равновесия сил,
действующих на звено 5 в векторном
виде (4), вычертив соответствующий
силовой многоугольник.
3.5 СИЛОВОЙ АНАЛИЗ ГРУППЫ АСУРА ВВВ
На группу действуют известные внешние силы: силы тяжести звеньев G 2
и G3 , силы инерции F2и и F3и , моменты сил инерции М 2и и М 3и .
Реакция в точке С со стороны группы Асура 4-5 уже известна по модулю и
направлению, т.к.
R43 R34

9.

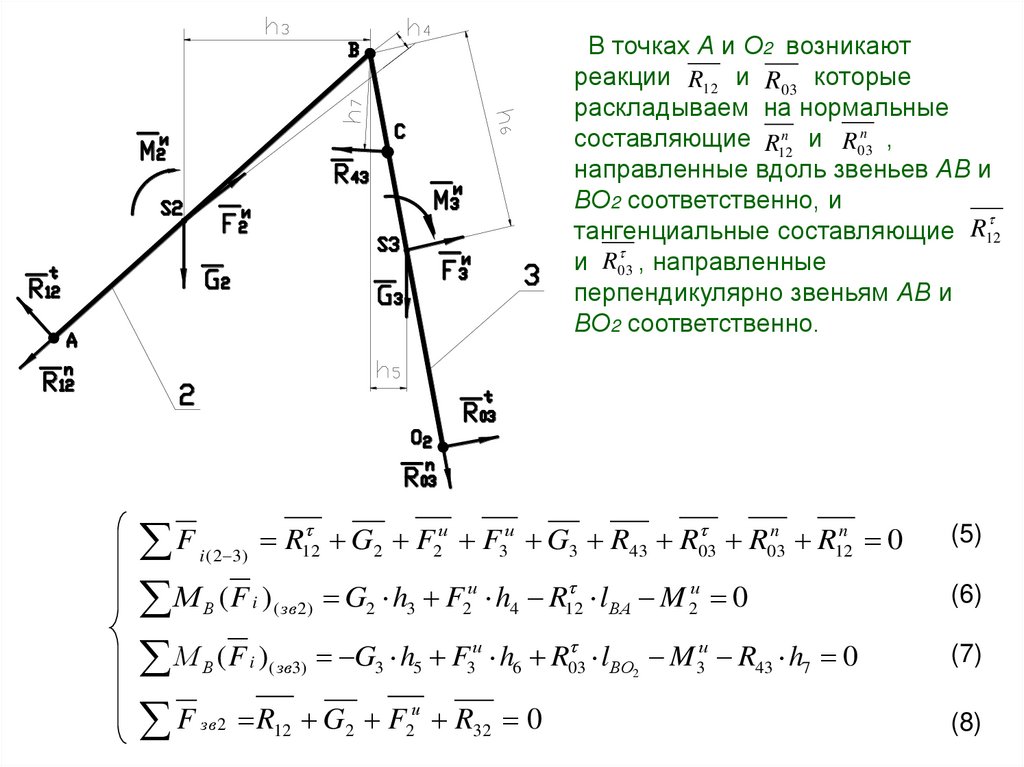
В точках А и О2 возникают
реакции R12 и R03 которые
раскладываем на нормальные
составляющие R12n и R03n ,
направленные вдоль звеньев АВ и
ВО2 соответственно, и
тангенциальные составляющие R12
и R03
, направленные
перпендикулярно звеньям АВ и
ВО2 соответственно.
F R G F F G R R R R 0
М ( F ) G h F h R l M 0
М
(
F
)
G
h
F
h
R
l M R h 0
F R G F R 0
i ( 2 3)
12
2
В
i ( зв 2 )
2
В
i ( зв3)
зв 2
12
3
2
и
2
3
и
2
5
и
3
и
2
32
и
3
3
4
12
6
03
43
03
ВА
и
2
ВО2
и
3
n
03
43
n
12
7
(5)
(6)
(7)
(8)

10.

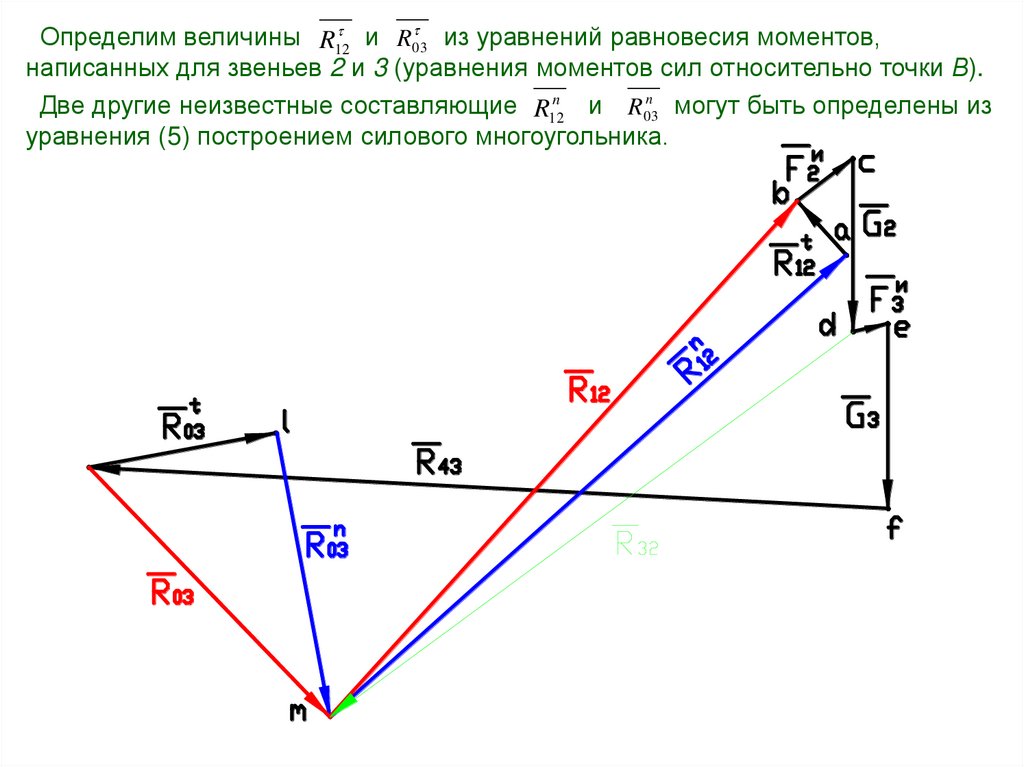
Определим величины R12
и R03
из уравнений равновесия моментов,
написанных для звеньев 2 и 3 (уравнения моментов сил относительно точки В).
Две другие неизвестные составляющие R12n и R03n могут быть определены из
уравнения (5) построением силового многоугольника.

11.

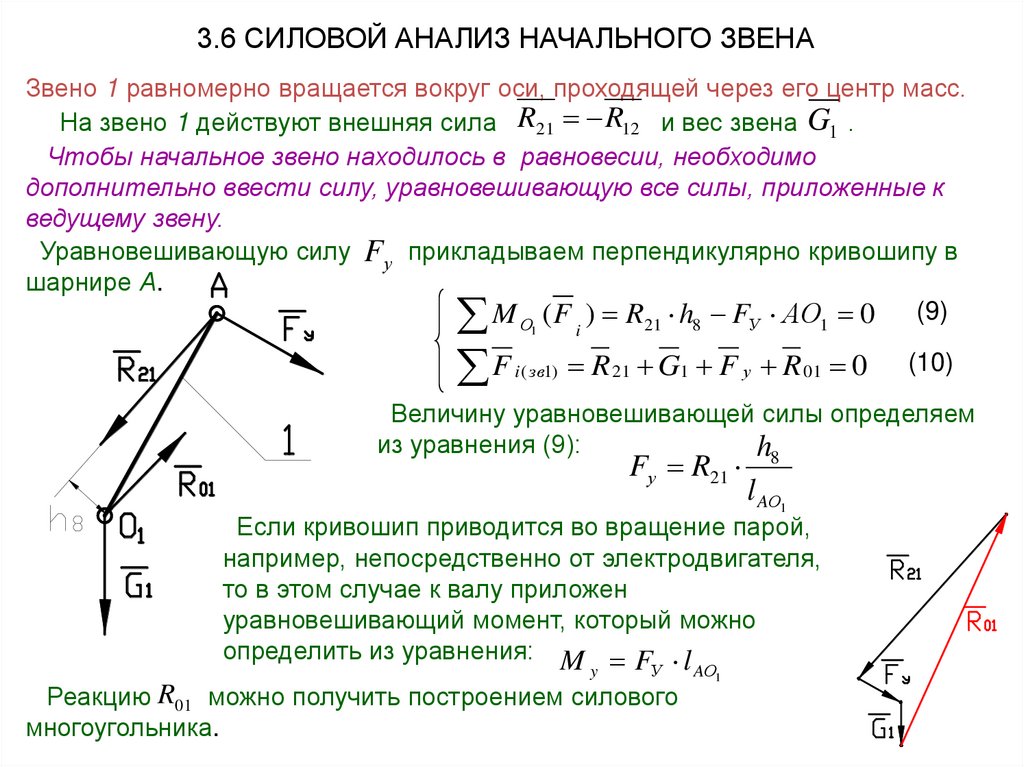
3.6 СИЛОВОЙ АНАЛИЗ НАЧАЛЬНОГО ЗВЕНА
Звено 1 равномерно вращается вокруг оси, проходящей через его центр масс.
На звено 1 действуют внешняя сила R21 R12 и вес звена G1 .
Чтобы начальное звено находилось в равновесии, необходимо
дополнительно ввести силу, уравновешивающую все силы, приложенные к
ведущему звену.
Уравновешивающую силу F у прикладываем перпендикулярно кривошипу в
шарнире А.
M О ( F ) R21 h8 FУ АО1 0 (9)
F
1
i ( зв1)
i
R 21 G1 F у R 01 0
(10)
Величину уравновешивающей силы определяем
из уравнения (9):
h8
Fу R21
l AО1
Если кривошип приводится во вращение парой,
например, непосредственно от электродвигателя,
то в этом случае к валу приложен
уравновешивающий момент, который можно
определить из уравнения: M F l
y
У
Реакцию R01 можно получить построением силового
многоугольника.
AО1

12.

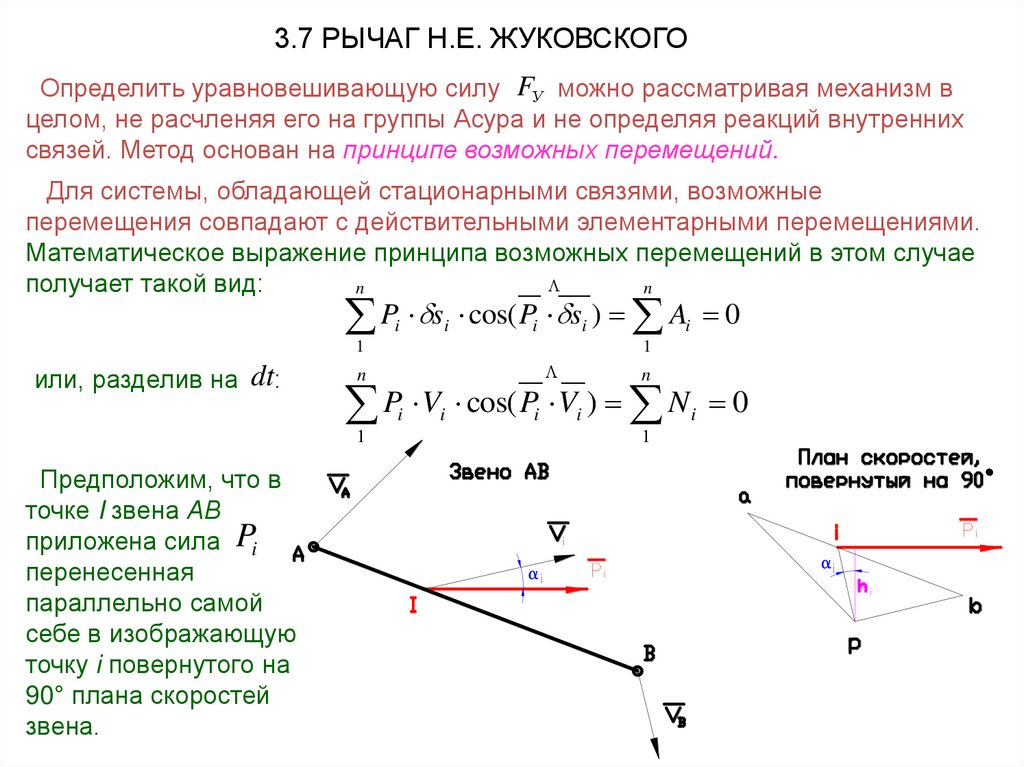
3.7 РЫЧАГ Н.Е. ЖУКОВСКОГО
Определить уравновешивающую силу FУ можно рассматривая механизм в
целом, не расчленяя его на группы Асура и не определяя реакций внутренних
связей. Метод основан на принципе возможных перемещений.
Для системы, обладающей стационарными связями, возможные
перемещения совпадают с действительными элементарными перемещениями.
Математическое выражение принципа возможных перемещений в этом случае
получает такой вид:
n
n
P s cos( P s ) A 0
i
i
i
i
1
или, разделив на dt:
n
n
P V cos( P V ) N 0
i
1
Предположим, что в
точке I звена АВ
приложена сила Pi
перенесенная
параллельно самой
себе в изображающую
точку i повернутого на
90° плана скоростей
звена.
i
1
i
i
i
i
1

13.

Мощность
N i силы Pi можно выразить следующим образом:
N i Pi Vi cos i Pi pi v cos i Pi hi v
hi — перпендикуляр, опущенный из полюса р плана скоростей на линию
действия силы.
Так как полученное выше уравнение, определяющее величину N i , имеет
место для всех сил Pi действующих на другие звенья механизма, то будем
n
n
иметь:
N P h 0
i
Поскольку v 0 , то
v
i
1
i
1
n
P h 0
i
i
1
На этом основан метод рычага Жуковского.
Для рассматриваемого механизма строится план скоростей и поворачивается
на 90° в сторону вращения кривошипа. В соответствующих точках плана
скоростей прикладываются внешние силы. Полученный чертёж рассматриваем
как жёсткий рычаг, вращающийся вокруг полюса р (рычаг Жуковского). Записав
уравнение равновесия рычага найдём уравновешивающую силу
.

14.

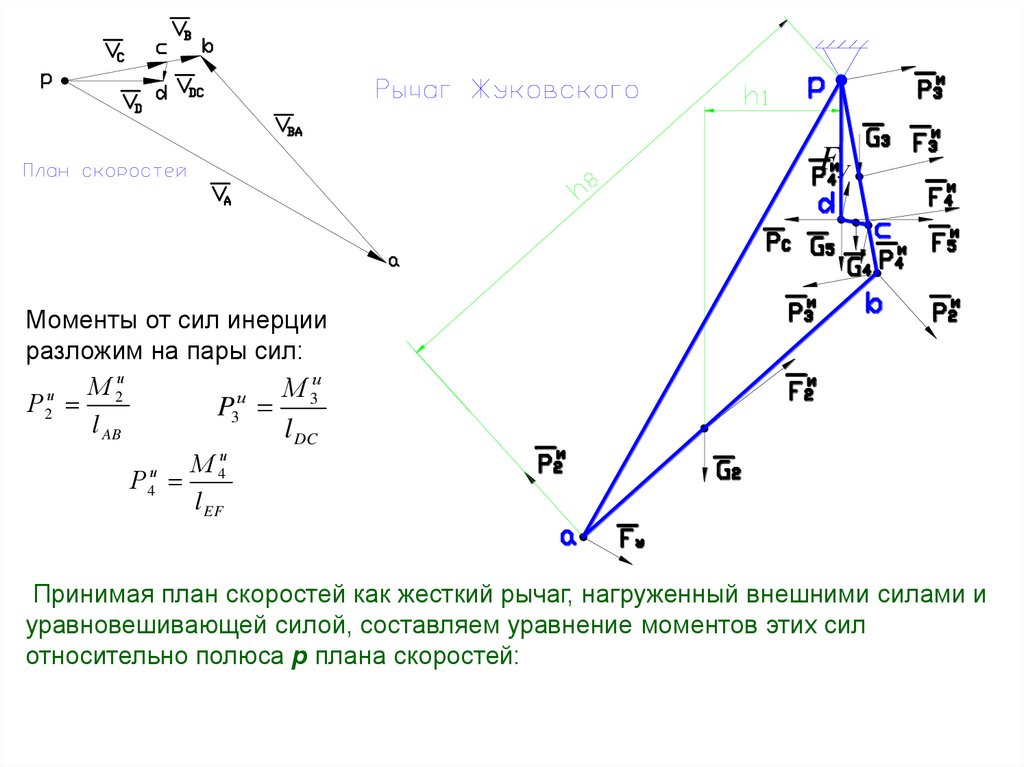
FУ
Моменты от сил инерции
разложим на пары сил:
М 2и
М 3и
и
и
Р2
P3
l AB
l DC
М 4и
Р
l EF
и
4
Принимая план скоростей как жесткий рычаг, нагруженный внешними силами и
уравновешивающей силой, составляем уравнение моментов этих сил
относительно полюса р плана скоростей:

15.

и
М
(
F
)
G
h
G
h
G
h
(
F
i
р
2
1
3
2
4
3
5 PC ) pf
F3и h4 F4и h5 F2и h6 Р3и h7 P2и h8 P2и h9
P4и h10 P4и h11 FУ рa 0
Из этого уравнения определяем величину уравновешивающей силы:
( PC F5и ) pf G2 h1 G3 h2 G4 h3 F3и h4
FУ
ра
F4и h5 F2и h6 Р3и h7 P2и h8 P2и h9 P4и h10 P2и h11
pа
Метод рычага Жуковского является более точным, т.к. погрешность
построений не накапливается, как в методе планов сил.
Метод планов позволяет определить не только уравновешивающую силу, но
и реакции в связях механизма, что важно знать при дальнейшем
конструировании и расчёте механизма и его элементов.
Сравним значения уравновешивающей силы, полученные двумя методами:
FУ ( Р. Ж .) FУ ( пл)
FУ ( Р. Ж .)
100%