Similar presentations:
12-дәріс
1. Нүкте динамикасының жалпы теоремалары
2. Материялық нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема
3. Анықтамалар: Нүктенің массасы мен жылдамдығының көбейтіндісіне тең векторын материялық нүктенің қозғалыс мөлшері деп атаймыз.
Анықтамалар:Нүктенің массасы мен жылдамдығының
көбейтіндісіне тең q mv векторын
материялық нүктенің қозғалыс мөлшері
деп атаймыз.
Күштің элементар уақыт аралығына
көбейтіндісін F dt күштің элементар
импульсі деп атаймыз. Ал одан алынған
t
F dt
интегралды
күштің [0,t] уақыт
0
аралығындағы импульсі деп атаймыз.
4. Динамиканың негізгі заңын қолданамыз
ma F ;dv
a
;
dt
d mv
F ; d mv Fdt (1)
dt
Материялық
нүктенің
қозғалыс
мөлшерінің
элементар өзгеруі осы нүктеге әсер етуші күштің
элементар импульсіне тең.
5. (1) теңдеуді [0,t] уақыт аралығында интегралдаймыз;
tmv mv0 Fdt
(2)
0
Материялық нүктенің шекті уақыт аралығындағы
қозғалыс мөлшерінің өзгеруі осы нүктеге әсер
етуші күштің сол уақыт аралығындағы импульсіне
тең.
6.
r xi yj zkv x i y j z k
F Fx i Fy j Fz k
t
mx mx 0 Fx dt
0
t
my my 0 Fy dt
0
t
mz mz 0 Fz dt
0
7. Жалпы түрде
F F x, y, z, x , y , z , tЕгер күш уақыттың
функциясы болса, онда
mx mx 0 S x t
my my 0 S y t
mz mz 0 S z t
F F t
t
Мұндағы
S x Fx dt
0
t
S y Fy dt
0
t
S z Fz dt
0
8. Интегралдау арқылы табатынымыз:
t1
x x0 x 0 t S x dt
m0
t
1
y y0 y 0 t S y dt
m0
t
1
z z 0 x 0 t S z dt
m0
9. Материялық нүктенің қозғалыс мөлшері моментінің (кинетикалық моментінің)өзгеруі туралы теорема
10.
Анықтамалар:M0 r F,
- күштің О центріне қатысты моменті,
l0 r mv , - нүктенің О центріне қатысты қозғалыс
мөлшері моменті.
Динамиканың негізгі заңын қолданамыз
ma F ;
r ma r F ;
11.
dv ddr
r mv mv ;
Түрлендіреміз: r ma r m
dt dt
dt
dr
v;
dt
Сондықтан:
r ma
v mv 0;
d
r mv ;
dt
Анықтамаларға сәйкес алатынымыз
dl 0
M0
dt
Материялық нүктенің кез келген О центріне қатысты
қозғалыс мөлшері моментінен уақыт бойынша
алынған туындысы осы нүктеге әсер етуші күштердің
сол центрге қатысты моментіне тең.
12.
ij
k
i
d
x
y
z x
dt
mx my mz Fx
j
k
y
z
Fy
Fz
Бірінші жолдың элементтері бойынша анықтауышты жіктеп,
i , j, k бірлік векторларының коэффициенттерін теңестірем
d
m yz zy yFz zF y
dt
Материялық нүктенің кез келген
өске қатысты қозғалыс мөлшері
d
уақыт
бойынша
m zx xz zFx xFz моментінен
алынған туындысы осы нүктеге
dt
d
m xy yx xFy yFx
dt
әсер етуші күштердің
қатысты моментіне тең.
сол
өске
13.
Центрлік күшті қарастырайық: Күштің әсер ету сызығыбойынан алынған нүктеге қатысты моменті әр қашан
нөлге тең.
l0 r mv const
бұдан үш алғашқы интегралды оңай алға болады:
m yz zy С1
m zx xz С2
m xy yx С3
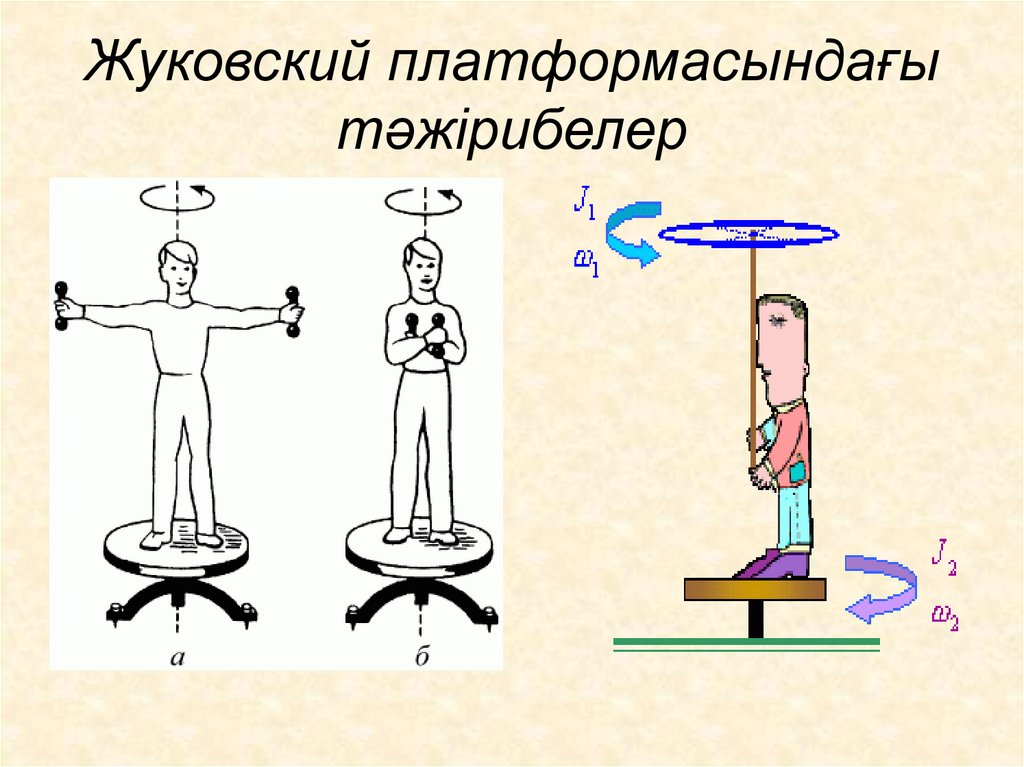
14. Жуковский платформасындағы тәжірибелер
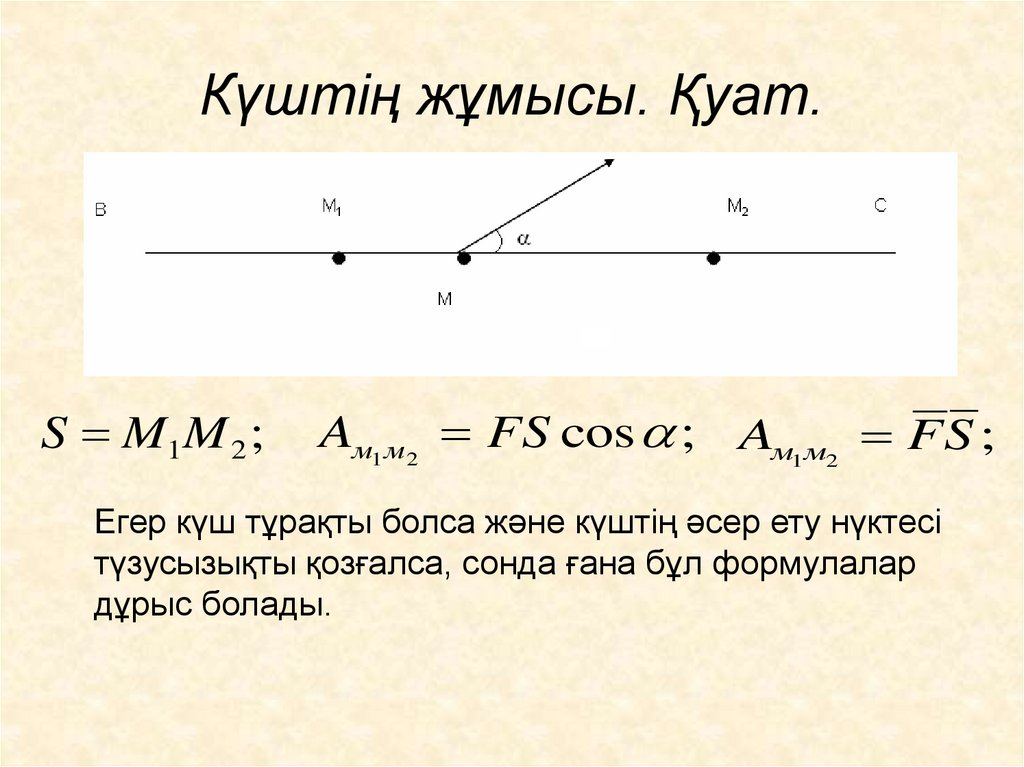
15. Күштің жұмысы. Қуат.
S M 1M 2 ;Aм1 м2 FS cos ; Aм1 м2 FS ;
Егер күш тұрақты болса және күштің әсер ету нүктесі
түзусызықты қозғалса, сонда ғана бұл формулалар
дұрыс болады.
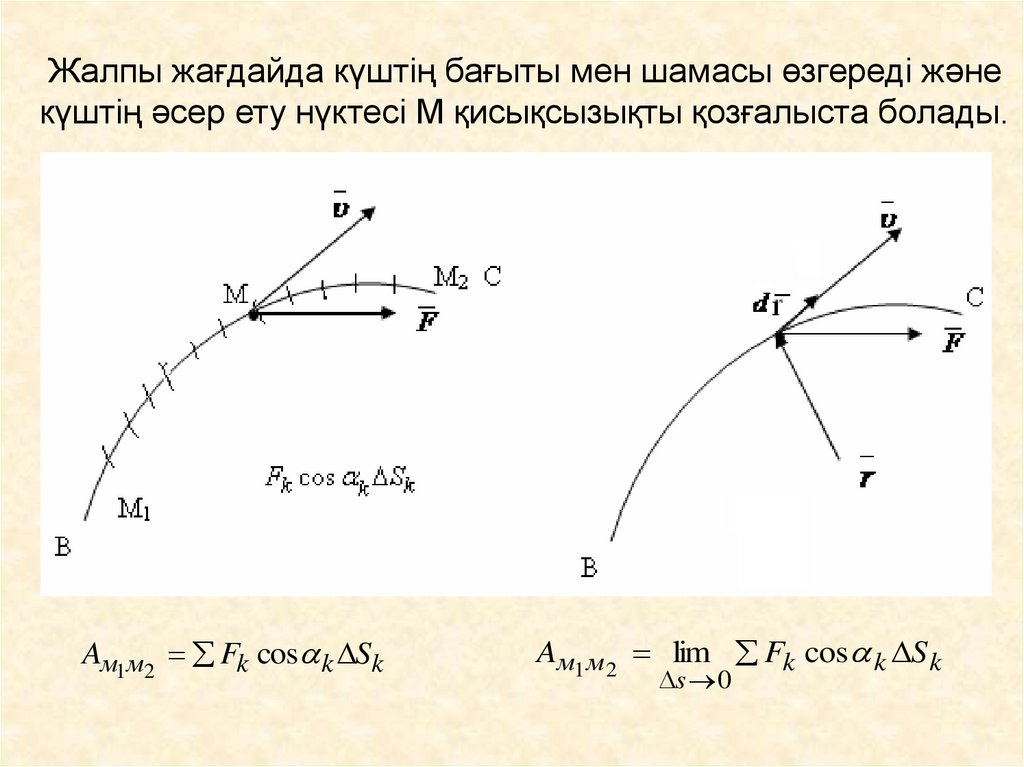
16. Жалпы жағдайда күштің бағыты мен шамасы өзгереді және күштің әсер ету нүктесі М қисықсызықты қозғалыста болады.
Aм1 м2 Fk cos k SkAм1 м2 lim Fk cos k S k
s 0
17.
Бұл шек бірінші ретті қисық сызықты интеграл деп аталадыA
F cos ds Бұдан екінші ретті қисық сызықты
интегралға өтеміз
м1 м2
dA F cos ds F күшінің элементар жұмысы.
dA F dr cos Fdr ,
Олай болса
Aм1 м 2
dr v dt
dA Fx dx Fy dy Fz dz, интегралдаймыз
Fx dx Fy dy Fz dz - екінші ретті қисық
м1 м 2
сызықты интеграл.
18.
Егер x x t , y y t , z z t ; болса ондаt2
Aм1 м2 Fx x Fy y Fz z dt
t1
Егер материялық нүктеге бірнеше F1 , F2 ,...Fn күштері
әсер етсін.
Материялық нүктенің әсер етуші тең әсерлі күштің кез
келген орын ауыстыру кезіндегі жұмысы құрамдас
күштердің
сол
орын
ауыстыру
кезіндегі
жұмыстарының қосындысына тең
A A1 A2 ... An .
19.
Дербес жағдайлар: F constr2
Aм1 м2 F dr F dr F r2 r1
м1 м2
r1
r2 r1 м1 м2
Aм1 м2 F м1 м2 F s cos
Ауырлық күшінің жұмысы
s cos Aм1 м2 р
20. Қуат
AF dx F dy F dz
x
y
z
м1 м 2
Егер F уақыт бойынша өзгерсе, онда
t2
A t Fx x Fy y Ft z dt
t1
Яғни жұмыс уақыт функциясы болса
F күшінің N қуаты деп жұмыстың өзгеру жылдамдығын
айтамыз.
A dA
N lim
.
t 0 t
dt
21.
dA t Fx x Fy y Ft z dt F x dx Fy dy Fz dzdA t F dr .
N
dA
dr
F
немесе N F Fx x Fy y Fz z
dt
dt
t2
Aм м2 N t dt
t1
A
N
t
(егер жұмыс бір қалыпта өзгерсе).
N 1Вт 1 Дж
сек
22. Материялық нүктенің кинетикалық энергиясының өзгеруі туралы теорема
23.
Анықтама:Нүктенің массасы мен жылдамдығының квадратының жарым
көбейтіндісі материялық нүктенің кинетикалық энергиясы
m 2
деп аталады.
T
2
d
d
m
F,
dt
m
dt
dr F dr
m 2
d
dr
m
dr m d m d d
dt
dt
2
m 2
dA
d
2
Материялық нүктенің кинетикалық
энергиясының толық
дифференциялы осы нүктеге әсер
етуші барлық күштердің элементар
жұмысына тең
24.
d mN
dt 2
2
Материялық нүктенің кинетикалық
энергиясынан уақыт бойынша алынған
толық туынды сол нүктеге әсер етуші
күштердің қуаттарының қосындысына
тең.
2
2
m 2
m
m
2
1
dA
d
Aм1 м2
2
м1 м2
м1 м 2
2
2
Материялық нүктенің бастапқы орнынан
соңғы орнына орын ауыстыру кезіндегі
кинетикалық энергиясының өзгеруі, осы нүктеге
әсер етуші күштердің сол орын ауыстыру
кезіндегі жұмыстарының қосымдысына тең.




![(1) теңдеуді [0,t] уақыт аралығында интегралдаймыз; (1) теңдеуді [0,t] уақыт аралығында интегралдаймыз;](https://cf5.ppt-online.org/files5/slide/r/Rjyc3rm1SAbp2KevYtq06gQZTu7CwfEVsFXIGD/slide-4.jpg)
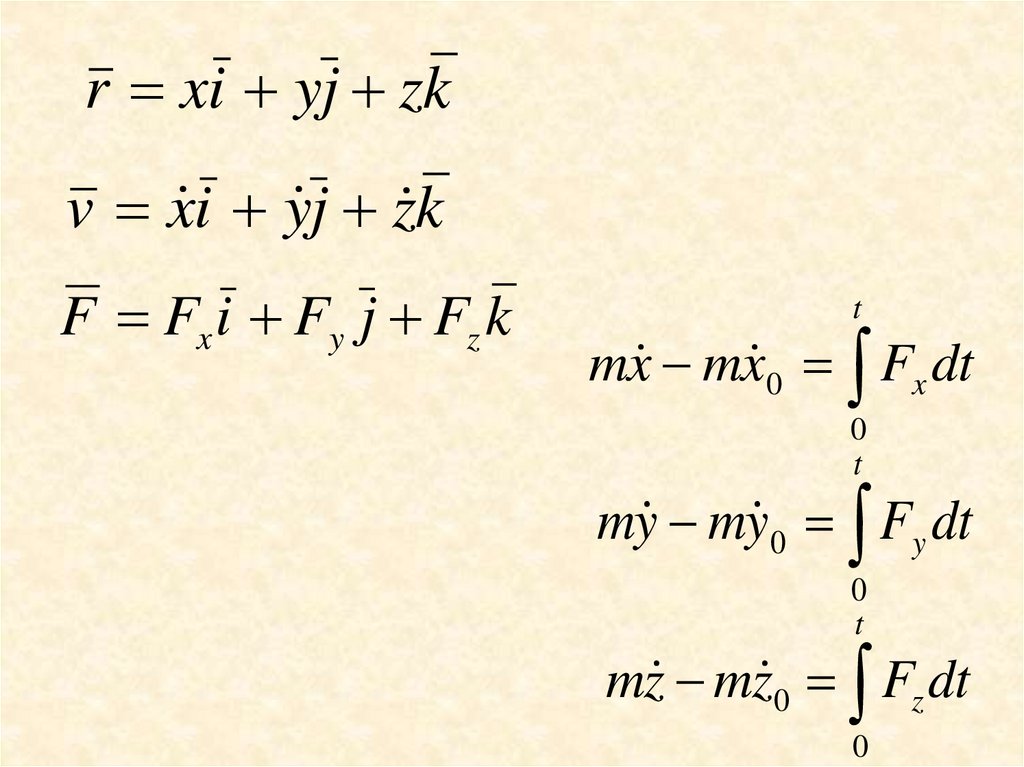
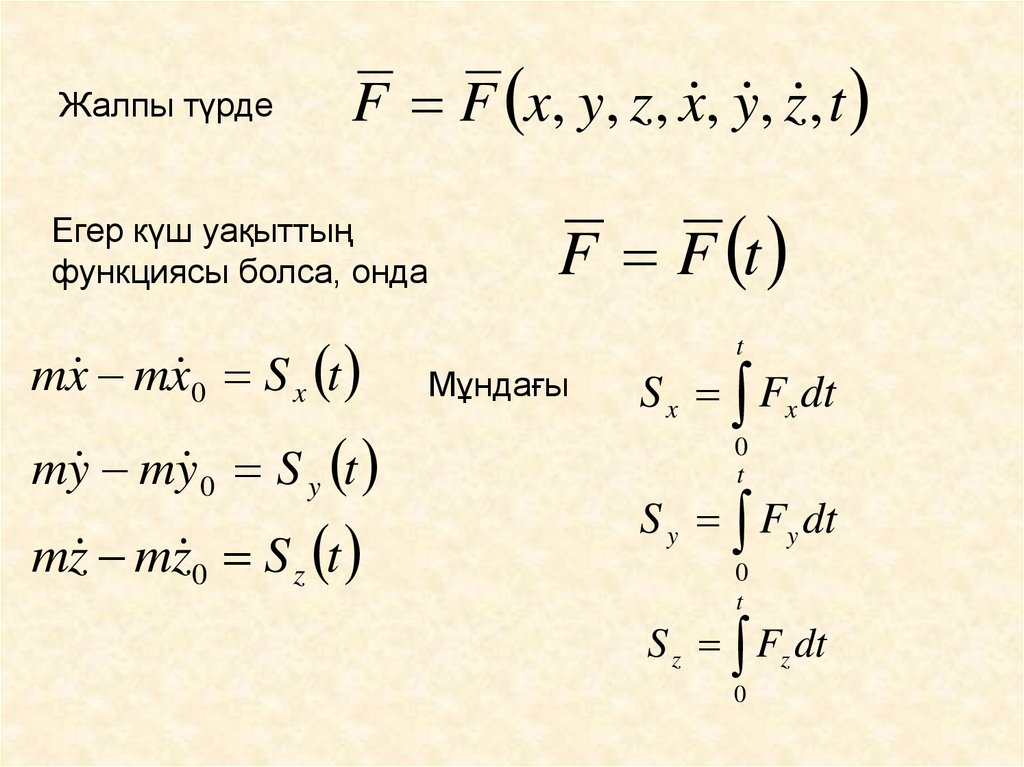
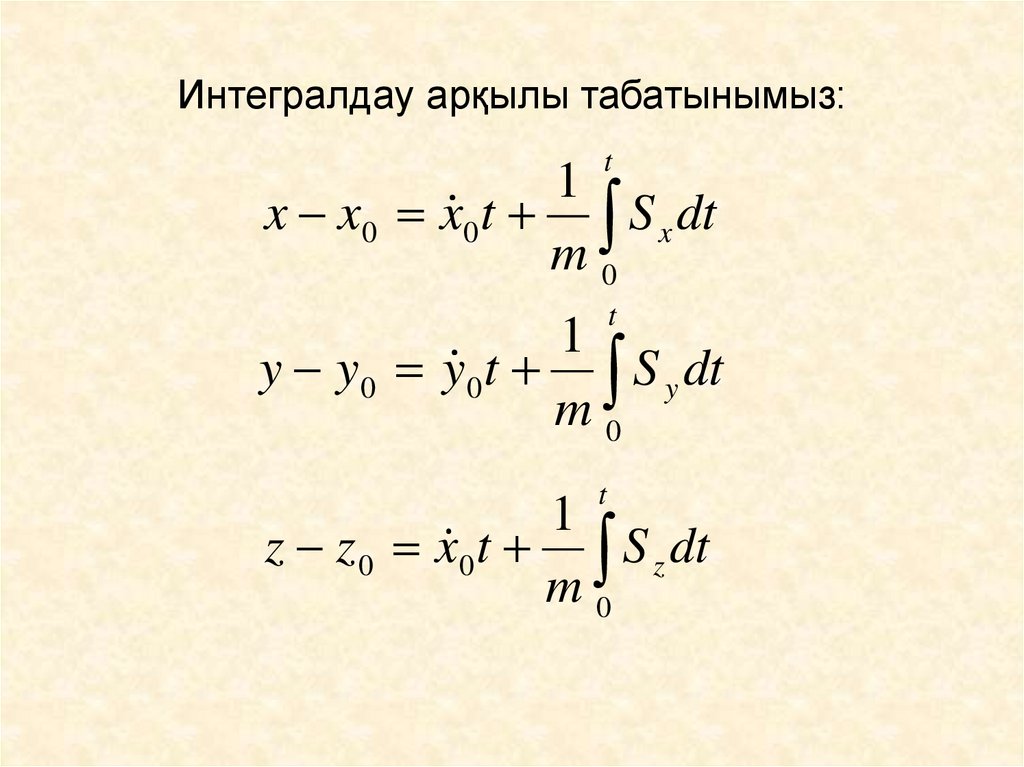









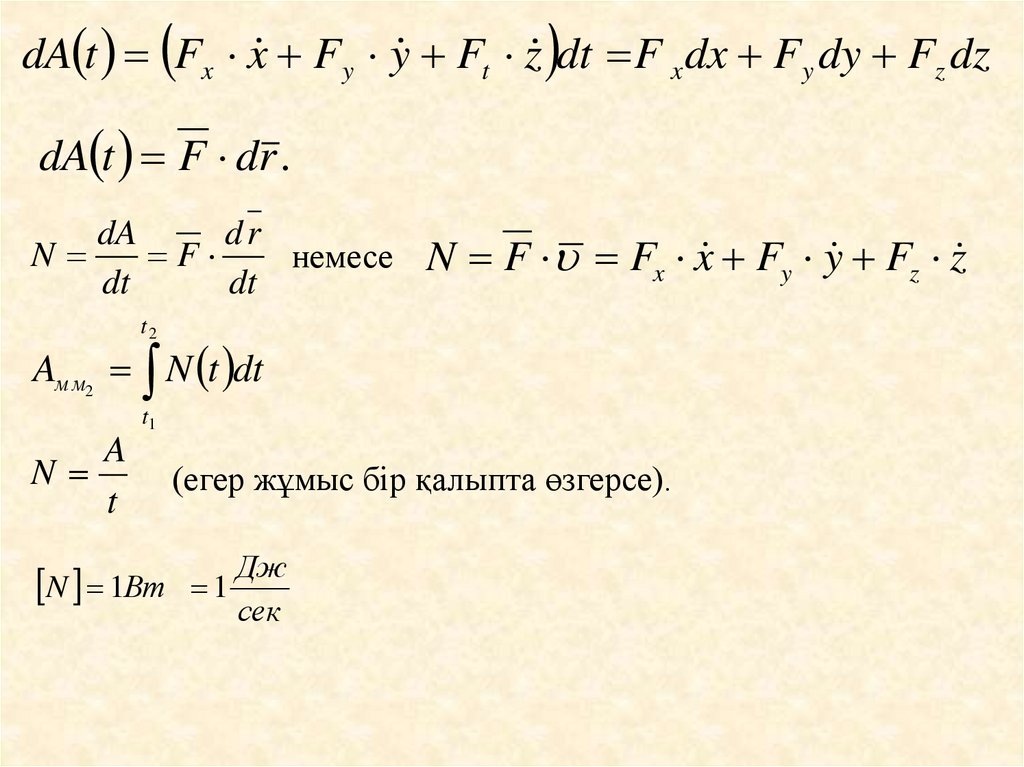



 physics
physics








