Similar presentations:
4.1
1. ПОНЯТИЕ ЛОГАРИФМА
2. Определение логарифма
Логарифмом числа b по основанию аназывается показатель степени,
в которую нужно возвести а, чтобы
получить b.
log a b c ,
a 0,
a b,
a 1,
c
b 0
3.
Определение логарифмаПримеры:
b >0
a>0, a≠1
c
b=a
log216=4,
log42=1/2,
log 1 27 3 ,
с = loga b
3
.
log0,254=
4. При каких значениях х существует логарифм
log x 3Х>3
log 10 x
X< 10
log 3x
X<0
log 2 x
X R
log x
Не существует ни при
каком х
1
4
5
5
5
2
0, 2
4
1, 3
5. Виды логарифмов
ОбыкновенныеНатуральные
Десятичные
6. Примеры
log 2 83 , т.к.
2 8
log 5 25 2 , т.к.
5 25
log 2 2
1 , т.к.
2 2
1
log 2 1, т.к.
2
1
2
2
1
2
3
9
1
log 3
9
2 , т.к.
3
2
1
1
7. Запишите в виде логарифмического равенства:
3 81log 3 81 4
1
32
1
log 2
5
32
3
1
log 1
3
64
4
4
2
5
1
1
64
4
3
4
125 5
16 8
3
1
log125 5
3
3
log16 8
4
(по
определению);
(по
определению);
8. Найдите число x
log 5 x 22
25
x 5
log 3 x 1
1
xx 31
3
log 1 x 2
6
2
1 2
x
6
xx 36
6
log 5 x 0
51
x
x
0
9. Найдите число x
log x 81 4x 3
4
3 81
1
log x
2
16
log 1 x 2
1
log x 2
4
6
2
1 2
x
6
xx 36
6
2
1
1
x
x
44
1
2x
2 4
2
10. Вычислите
1log 2 0,25 log 2 2
4
log 1 3
3
3 log 1 3 3
3
1
1
2
log 1 3
3
1
2
3
2
1
log 1 3 log 1
3
3
3
3
2
3
2
11. Вычислите
13 log 7 3 1 2
7
4
2 log 5 0,04 2 log 5
100
1
2 log 5
2 2 4
25
12. ОСНОВНОЕ ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВО
aloga b
b
( где b>0,a>0 и a ≠1)
13.
Вычислите письменно значения логарифмов:log 3 9
log 32 2
log 125 25
log10 0,01
1
log 2
8
1
log 3
3
log 27 9
log10 0,001
log 4 16
log 9 3
log 5 0,04
log 3 9
1
log 5
25
log 32 8
1
log 3
243
log 7 1
log 81 27
log10 100
log0 , 3 0 , 09
0,3
2
log 2 16









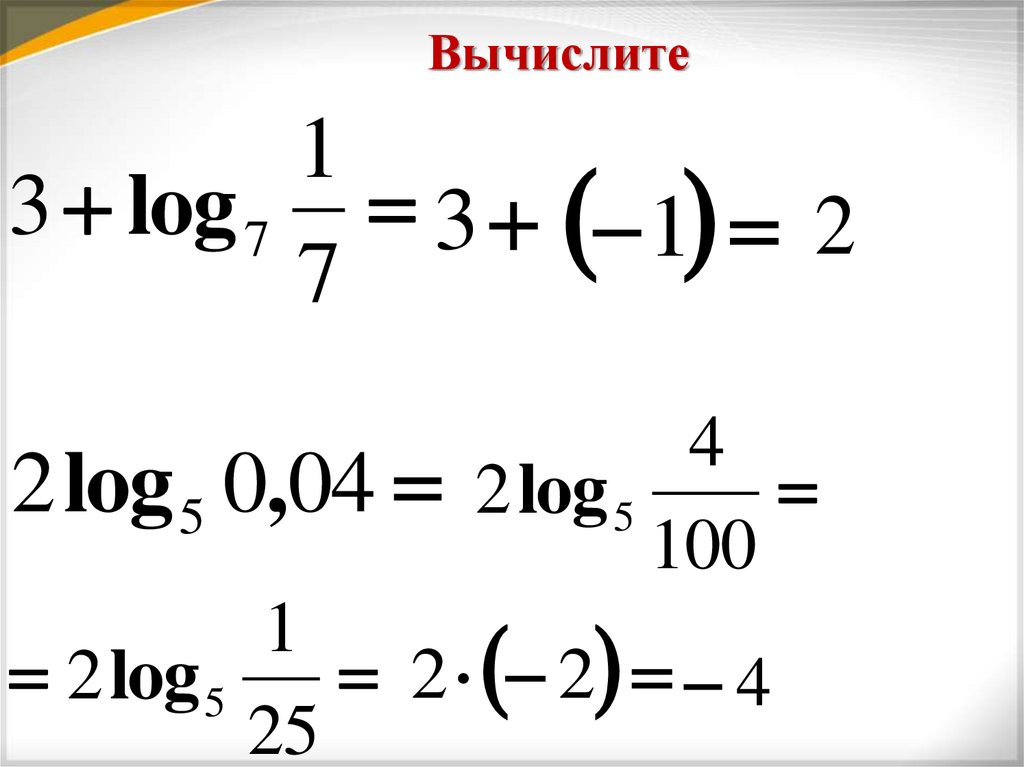





 mathematics
mathematics








