Similar presentations:
Тождественные преобразования логарифмических выражений
1.
Тождественные преобразованиялогарифмических выражений
Понятие логарифма
Понятие логарифма
Тождественные
преобразования
Свойства логарифмов
логарифмических выражений
Свойства логарифмов
2.
Логарифмы открытышотландским
математиком
Дж. Непером и
швейцарским
математиком
Й. Бюрги
в начале 17 в.
logos - отношение, соотношение и
arithmos - число
3.
«Изобретениелогарифмов, сокращая
вычисления нескольких
месяцев в труд
нескольких дней, словно
удваивает жизнь
астрономов».
Лаплас
4.
Для чего были придуманылогарифмы?
для ускорения вычислений
для упрощения вычислений
для решения
астрономических задач
5.
Определениеloga b
loga b
b > 0a b основное
p log x
a > 0log x логарифмическое
p
Тождественные преобразования
логарифмических выражений
Понятие логарифма
log a xy log a x log a y
p
тождество
b
log
b
log
a1
a
a
a
b
Свойства логарифмов
a
a
log aq x p log a x
q
6.
log a bb
a
Вычислите:
log
основное
логарифмическое
тождество
3
3
17
log 0,36
6
0,3
17
log
5
0,5
1
2
5
7.
log a blog a 1 0
log a a 1
означает,
что
x
a b
0
a 1
1
a a
x
Вычислите:
log 3 81 log 3 3 4
4
1
1
2
log 0,3
log 0,3 0,09 log 0,3 0,3
0,09
2
log 0,3 0,3 2
1
8.
Задание ЕГЭЕсли log a 8 3 и log b 243 5,
то чему равно a b ?
b 243
a3 83
5
5
b 3
a 2
b 3
a 2
a b 2 3 6
5
3
1)4
2)5
3)6
4)8
9.
log 10 x lg x - десятичный логарифмlog e x ln x - натуральный логарифм
lg 100 ?2
ln e ?5
lg 0,001 ? 3
1
ln 4 ? 4
e
5
10.
1log 2 14 log 2 (2 7) log 2 2 log 2 7
a b
1 log 2a7Свойства
log a xy> 0log axx 0log a y
aлогарифмов
1 y 0
Тождественные преобразования
логарифмических выражений
Понятие логарифма
Свойства логарифмов
loga b
loga b
log a xy log a x log a y
log a x p p log a x
p
log aq x p log a x
q
11.
Задание ЕГЭУпростите выражение
log 2 14 log 2 14 log 2 7 2 log 2 7
log 2 14 2 log 2 7
2
2
(1log
log 214
7)
1(1
log
7
)
log
7
2
log
7
2
2
2
log 2 7
2
(1 log 2 7) 2 log 2 7
2
2
1 2 log 2 7 log 2 7 log 2 7 log 2 7 2 log 2 7
1 log 2 7 2 log 2 7
2
a b
2
2 2 7 1
2
3 log
a 2ab b1
3 log 2 7 1
2
2
12.
a>0a 1
Свойства
логарифмов
x 0
y 0
3
Найдите значение логарифма: log c ,если
c
log c 3 4
log b
log b
3
a
b1
log c log xc 3 loglogc x c p log x log c 3 1
c log a log alog xx p log xlog a y
q
4 1 3 y
1)7
2)2,5
3) 1
4)3
a
Тождественные преобразования
логарифмических выражений
Понятие логарифма
a
log a xy log a x log a y
p
Свойства логарифмов
a
a
p
a
q
a
13.
Задание ЕГЭНайдите значение b по его логарифму
lg b lg log 7 343 lg 4
3
lg log 7 343 lg 4 lg log 7 7 lg 4
3
lg 3 lg 4 lg
4
3
b 0,75
4
1)3
2) 1
3)0,75
4)1
3
14.
a>0a 1
Свойства
логарифмов
log 5 49 log 5 7
7
log 3 5 log 3p 5 log x p log x
log x x p70log
p
Тождественные преобразования
логарифмических выражений
Понятие логарифма
Свойства логарифмов
a
2
log2
7
a blog
5
1 loga b
a 1 b
7
log 5
p
log a xy log a x log a y
a
a
log aq x log a x
q
p
3
a
x
15.
Задание ЕГЭ2
Вычислите log 3 (b : 27), если log 3 b 6
log 3 (b : 27) log 3 b log 3 27
3
3
log 3 b log 3 3 log 3 b 3
2
log 3 b 6
1
2 log 3 b 6 2
log 3 b 3
3 3 6
1) 6
2) 1
3) 9
4)0
16.
a>0a 1
Свойства
логарифмов
loga b
log16
ab
x 0
Выразить log 3 через
a
b
логарифм с основанием 2.
log x p logbx
p 3
log a2 3b > 0loglog
log 2 3
x 2log x
1 q 4
log 16 3
b
log 2 16 log 2 2b
4
Тождественные преобразования
логарифмических выражений
log x
log x
log a
Понятие логарифма
log a xy log a x log a y
p
Свойства логарифмов
a
a
p
a
q
a
17.
Задание ЕГЭВычислите:
2 log 3 8 log 2 3 2
log6 7
3
log6 7
log 2 8 3
2
log 2 3 2 3 log6 7
log 2 3
6 6
log6 7
7
6 7 1
18.
a>0a 1
Свойства
логарифмов
Тождественные преобразования
логарифмических выражений
a
x 0
q 0
loga b
loga b
b
1 1
x 5 log
x 35
log
log 27log
5 a q log
q 3
Понятие логарифма
Свойства логарифмов
log a xy log a x log a y
log a x p p log a x
3 log x p p log x a
3 aq q a
19.
Задание ЕГЭУпростите выражение:
6 log 8 9 2 log 2 3
2
6 log 23 3 2 log 2 3
2
6 log 2 3 2 log 2 3
3
4 log 2 3 2 log 2 3 2 log 2 3
1) 2 log 2 3
2) 6 log 2 3
3) 6
4) log 2 3
20.
Задание ЕГЭВычислите:
3 3
log16 3 3
7
4
2
2
log 2 3 3
log 2 3 3
7
4
72
42
log
3
3
log
3
3
2
2
7
4
7
4
log49
2
2
1
3 6q х log а х
log3 а х3 3р log
3 а х 2 log
а
q
р
21.
Тождественные преобразованиялогарифмических выражений
loga b
loga b
x
alogx xblog y
log log
log a log
a
b1 a 0
b
a
a1
y a px
xb
p log x
log
xlog
a
logalog
x q x alog
a log
p
log
x
x
plog
xy
log
x
y
log
x
a log
a
a
log
x
log
x
a
a
a
b
log a 1
Тождественные преобразования
логарифмических выражений
log a xy log a x log a y
Понятие логарифма
p
a
Свойства логарифмов
a
p
a
a
q
a
q
q
a
22.
Вычислите: log 5 125 log 5 251 способ: log 5 125 log 5 25
log 5 5 log 5 5 3 2 1 125
2 способ:log 5 125 log 5 25 log 5
1
25
3
2
Найдите значение выражения:
4
1
4
1
log 4 log 4 9 log 4 log 4 9 log 4 16
9
16
9
2
log 4 4x log 4 4 1 2 1 2 3
log a a x
log a xy log a x log a y
x
log a log a x log a y
y
23.
2 log2 3Вычислите:
4
4
2 log 3
log2 3
2
16 : 2
4 : 4
2 log2 3
2
16 : 2
a
loga b
log2 32
b
a :a a
x
y
16
7
16 : 9 1
9
9
log a x p log a x
p
x y
24.
1log 1
16
81
Найдите значение выражения:
1
1
1
1
log 1
log 2
log
16
9 16
2 9 16
81
9
9
9
(9
1
1
log
9 16
2
log a q
a
)
b
1
2
1 2
4
(
16
)
16
1
x log a x
q
loga b
19
a
b
x
b
a
x
25.
Найдите значение выражения:log 3 12 log 3 7 log 7 5 log 5 4
log 3 7 log 7 5 log 5 4
log 3 5 log 3 4
log 3 7
log 3 4
log 3 7 log 3 5
12
log 3 12 log 3 4 log 3 log 3 3 1
4
26.
Представьте в виде разности1
логарифмов: 1
((log 2 log 3 2) 2 2) 2
4
1
log
3
4
3
4
4
2
log 3 2 log 2 3 2 log 3 2
4
log 3 2
log 3 2 è log 22 3
4
4
2 2 log 3 2 1
1 1 è log 3log
4
log 3 2 4 2
32 4
log 3 2
log 3 2
2
2
4
4
log 3 2 1 log 3 2 1
2
4
log 3 2
log 3 2
4
3
4
2
27.
12
1
2
((log 2 log 3 2) 2)
1
1
log 4 2 1 2 2 log 4 2 1 2
3
3
2
2
2
2
log
2
log
2
3
3
1
1
2 2
2
4
2
log 3 2 1 2 log 3 2 2 log 3 2 1
2
2
1log 3 2
log
2
3
2
2
log 2 2 1
3
log 3 2
4
3
4
2 1
2
28.
12
2
log 2 1
log
2
1
3
log 3 2
log 3 2
0 log 3 2 1
2
0 log 3 2 1
2
2
1 log 3 2
log 3 2
1
1
log 3 2
log 3 2
log 3 2 log 3 2 log 3 2
log 2 3
log 3 2 log 2 3 log 3 2
log 2 2 1
1
1
4
4
((log 3 2 log 2 3 2) 2 2) 2 log 2 3 log 3 2
2
3
2
29.
Тождественные преобразованиялогарифмических выражений
Тождественные преобразования
логарифмических выражений
Понятие логарифма
Свойства логарифмов








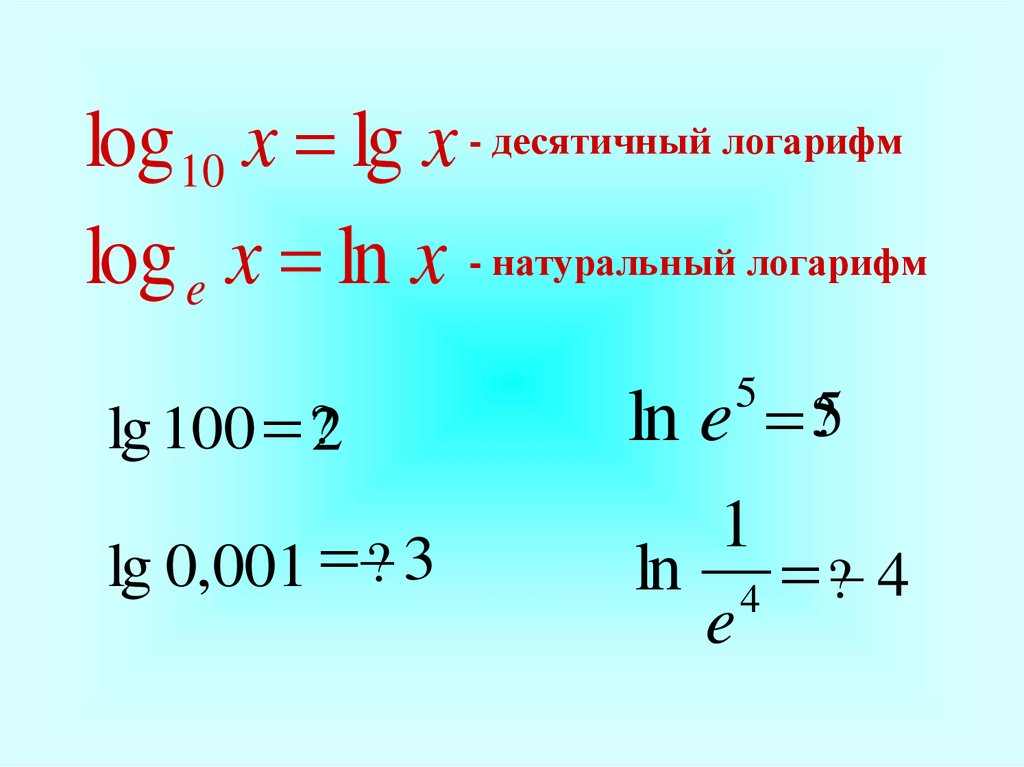



















 mathematics
mathematics








