Similar presentations:
Понятие логарифма. Определение логарифма
1. ПОНЯТИЕ ЛОГАРИФМА
2. Определение логарифма
Логарифмом числа b по основанию аназывается показатель степени,
в которую нужно возвести а, чтобы
получить b.
log a b c ,
a 0,
a b,
a 1,
c
b 0
3.
Определение логарифмаПримеры:
b >0
a>0, a≠1
c
b=a
с = loga b
log216=4,
log42=1/2,
log 1 27 , 3
3
log0,254=
.
4. Примеры
log 2 83 , т.к.
2 8
3
log 5 25 2 , т.к.
5 25
log 2 2
2 2
1 , т.к.
1
log 2 1, т.к.
2
1
log 3
9
2 , т.к.
2
1
2
3
1
2
1
2
1
9
5. Запишите в виде логарифмического равенства:
43 81 log 3 81 4 (по определению);
1
5
1
2
log 2
5
(по определению);
32
3
1
1
64
4
32
3
125 5
4
16 8
3
1
log 1
3
4 64
1
log125 5
3
3
log16 8
4
6. Особые логарифмы
Десятичныелогарифмы
(по основанию 10)
Натуральные
логарифмы
(по основанию е)
log 10 a lg a
log e a ln a
7. Пример
lg 1002, 10 100
lg 10
1, 10 10
lg 1
0, 10 1
lg 0,1
2
1
0
1, 10
lg 0,00001
1
5, 10
0,1
5
0,00001
8. Пример
ln e1,
e e
1
ln e 2, e e
1
1
1
ln 1, e
e
e
2
2
2
log e e 1
ln e
1
2
ln e
3
1
3
9. Найдите число x
log 5 x 22
25
x 5
log 3 x 1
1
1
xx 3
3
log 1 x 2
6
xx 36
6
2
1 2
x
6
log
5
x 0
51
x
x
0
10. Найдите число x
1log x
2
16
log x 81 4
x 3
1
x
4
т.к.3 81
4
2
1
1
т.к.
16
4
1
log x 2
4
x 2
т.к.2
2
1
4
11. Вычислите
1log 2 0,25 log 2 2
4
log 1 3 3 log 1 3 3
3
3
1
1
2
log 1 3
3
3
2
1
2
1
log 1 3 log 1
3
3
3
3
2
3
2
12. Вычислите
13 log 7 3 1 2
7
4
2 log 5 0,04 2 log 5
100
1
2 log 5
2 2 4
25
13. Основные свойства логарифмов
Основное логарифмическоетождество
1) a
2)
log a b
b
,
log a 1
3) log a a
0
1
a 0,
a 1,
b 0
14.
Основные свойства логарифмов4) log a (bс) log a b log a с
b
5) log a log a b log a с
с
6) log a b m m log a b
6 ) log a a m m
1
7) log ak b log a b
k
m
m
8) log ak b log a b
k
log c b
9) log a b
log c a
1
7 ) log ak a
k
m
m
8 ) log ak a
k
1
9 ) log a b
logb a
15. Понятие логарифмической функции
Функцию вида.
y = logaх, где а ≠ 1, a > 0, х > 0
называют
логарифмической функцией
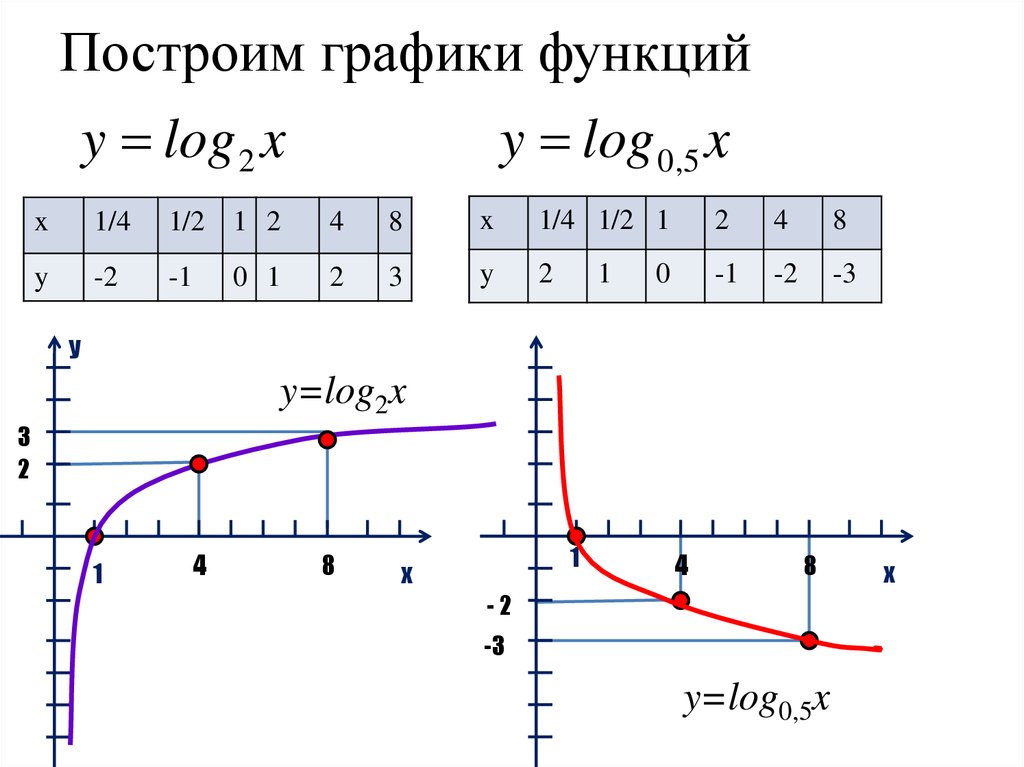
16. Построим графики функций
y log 2 xy log 0,5 x
x
1/4
1/2 1 2
4
8
x
1/4 1/2 1
2
4
8
y
-2
-1
2
3
y
2
-1
-2
-3
0 1
1
0
y
y=log2x
3
2
1
4
8
1
x
4
8
-2
-3
y=log0,5x
x
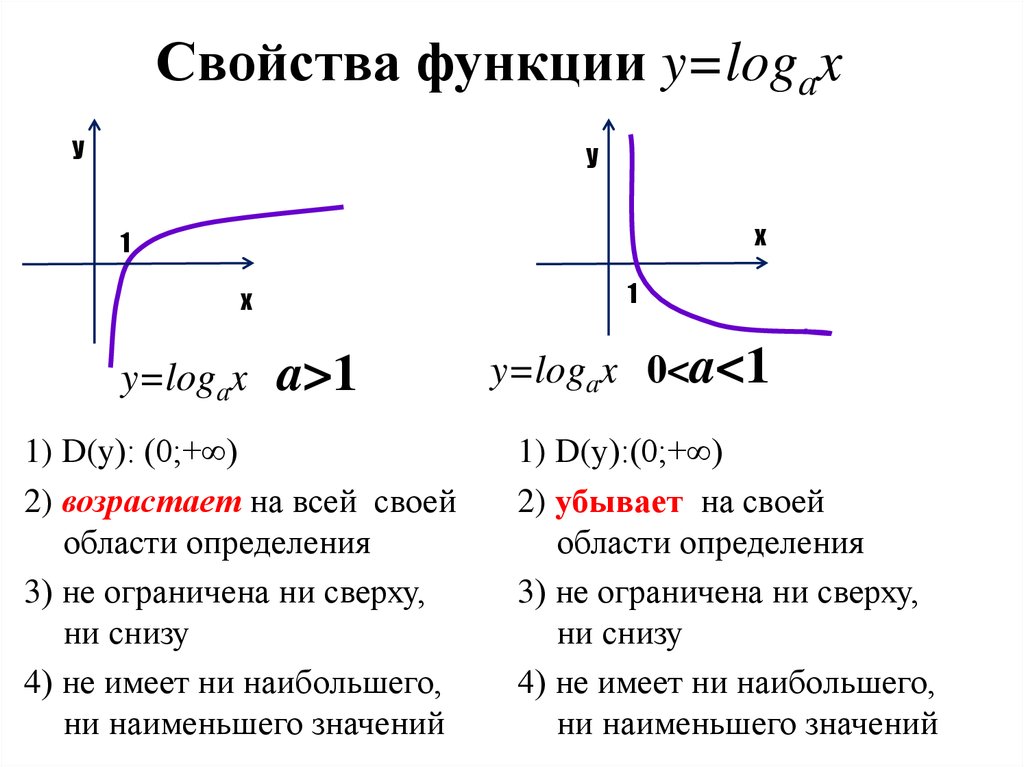
17. Свойства функции y=logax
yy
x
1
1
x
y=logax
a>1
1) D(y): (0;+∞)
2) возрастает на всей своей
области определения
3) не ограничена ни сверху,
ни снизу
4) не имеет ни наибольшего,
ни наименьшего значений
y=logax 0<a<1
1) D(у):(0;+∞)
2) убывает на своей
области определения
3) не ограничена ни сверху,
ни снизу
4) не имеет ни наибольшего,
ни наименьшего значений







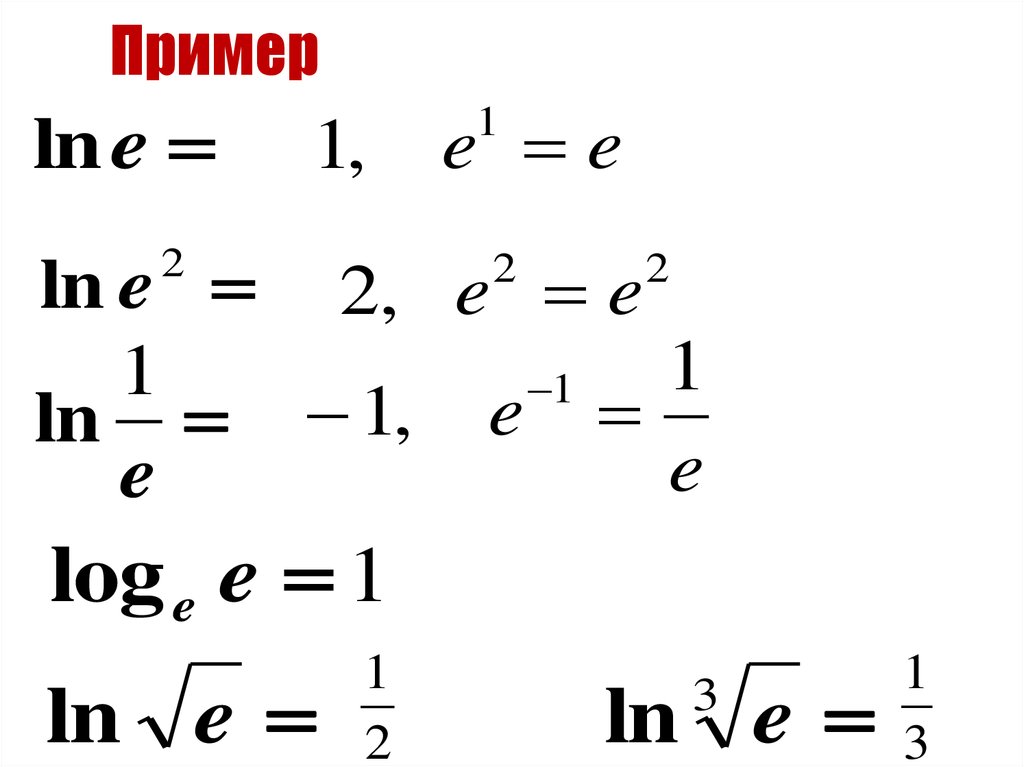
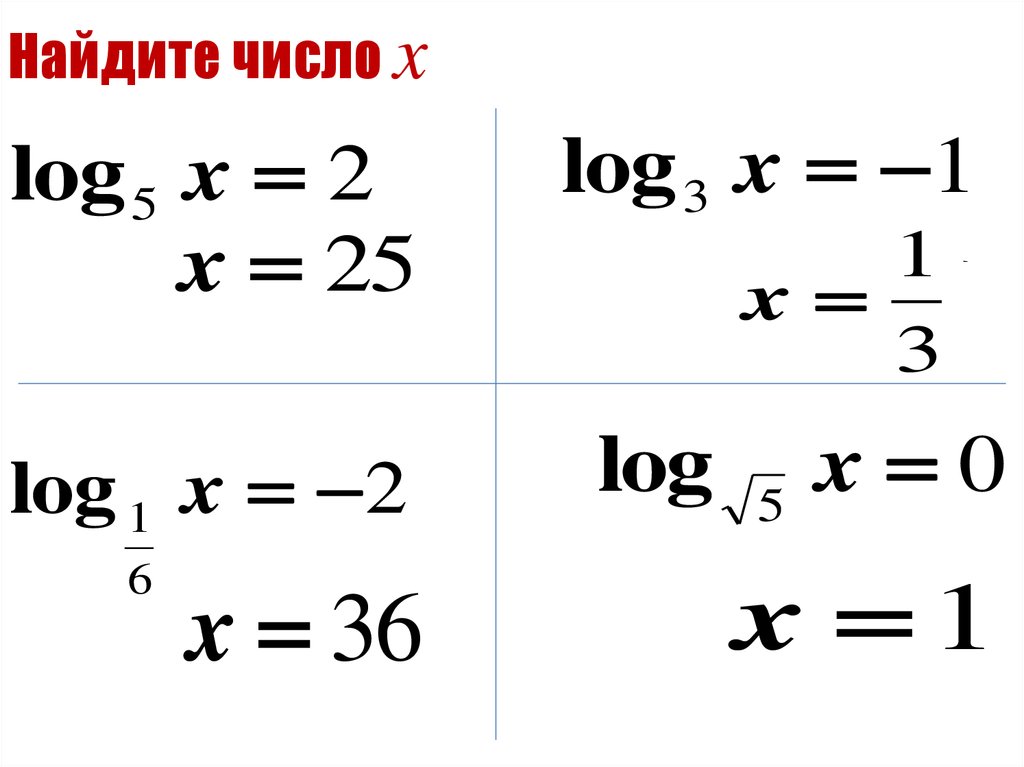

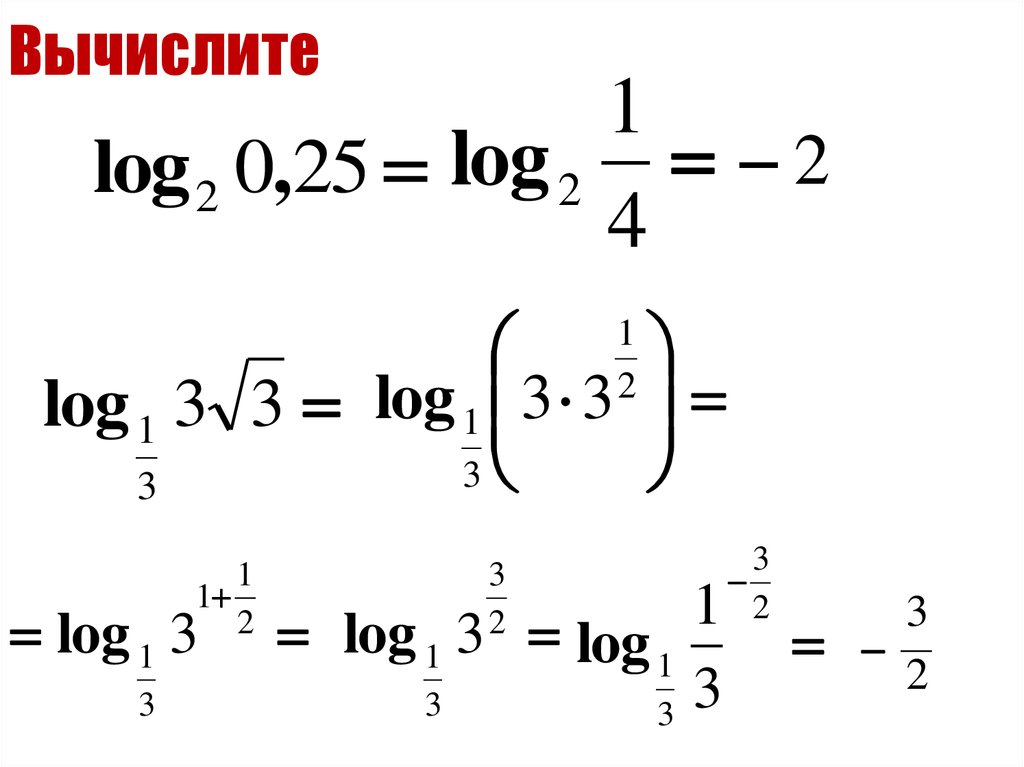
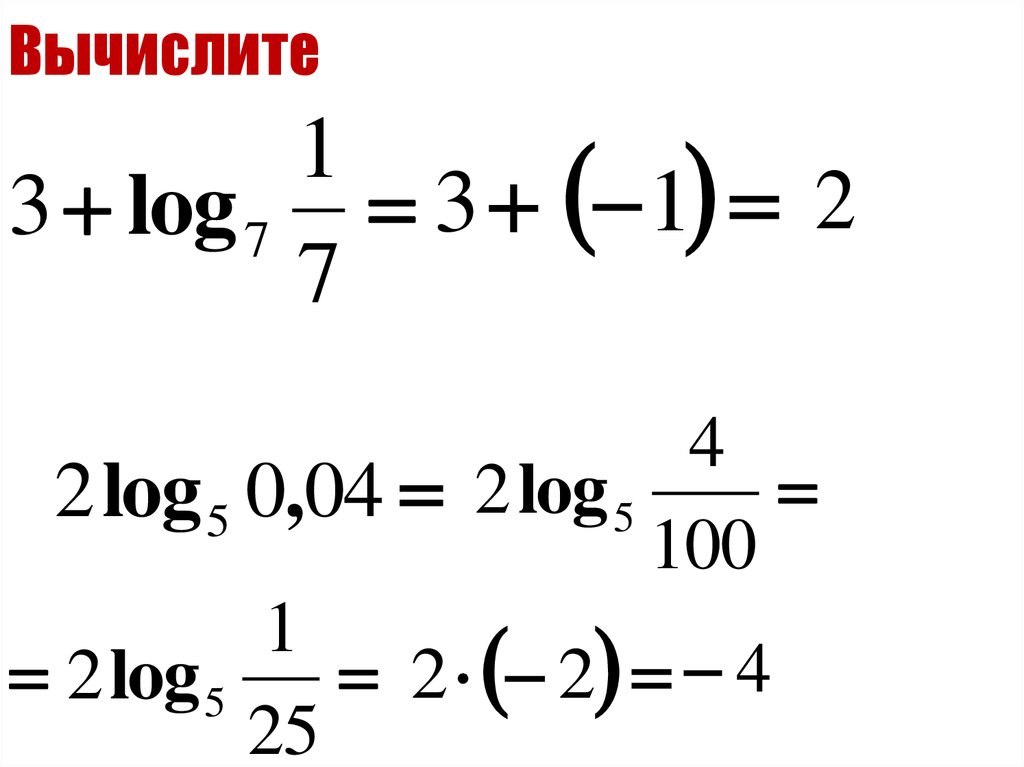



 mathematics
mathematics








