Similar presentations:
Логарифм числа. Определение логарифма
1.
ПОНЯТИЕЛОГАРИФМА
2.
Определение логарифмаЛогарифмом числа b по основанию а
называется показатель степени,
в которую нужно возвести а, чтобы
получить b.
log a b c ,
a 0,
c
a b ,
a 1,
b 0
3.
Определение логарифмаb >0
a>0, a≠1
c
b=a
с = loga b
Примеры:
log216=4,
log42=1/2,
log 1 27 3
3
log0,254=
.
,
4.
При каких значениях х существует логарифмlog x 3
Х>3
log 10 x
X< 10
1
4
5
log 3x
X<0
log 2 x
X R
5
5
2
0, 2
log x
4
1, 3
Не существует ни при
каком х
5.
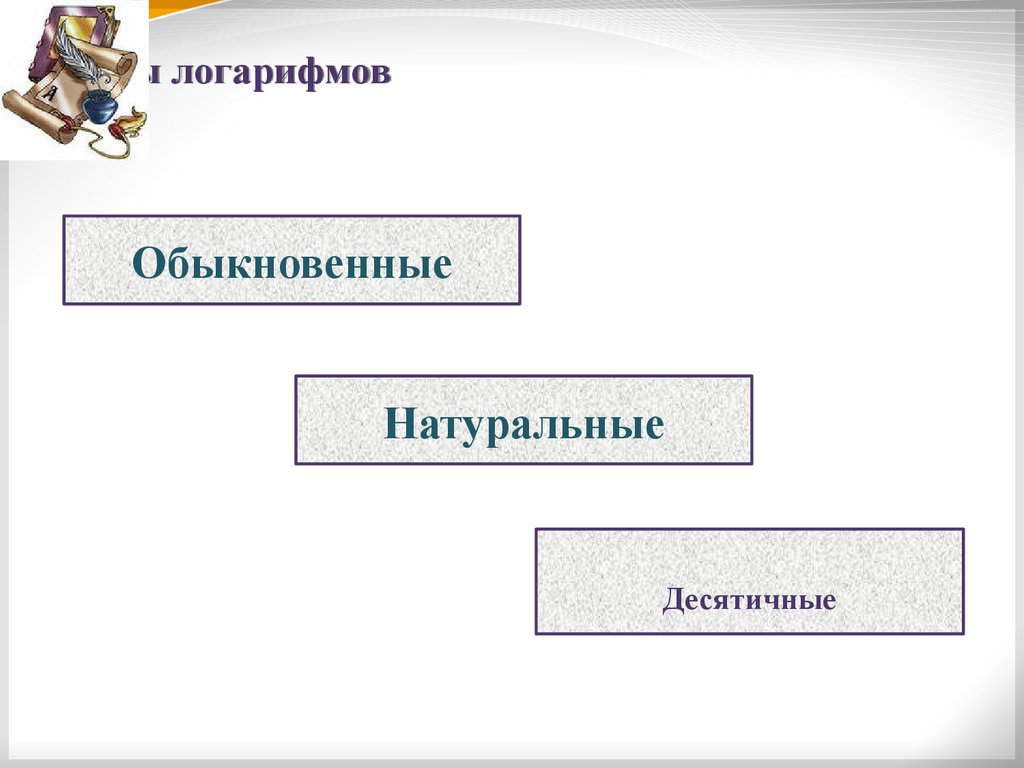
Виды логарифмовОбыкновенные
Натуральные
Десятичные
6.
Примерыlog 2 8 3 , т.к.
log5 25 2 , т.к.
log 2 2 1 , т.к.
1
log 2 1 , т.к.
2
1
log3 2 , т.к.
9
3
2 8
2
5 25
1
2 2
1
2
2
1
2
3
9
1
7.
Запишите в виде логарифмическогоравенства:
4
3 81
2
5
1
32
3
1
1
64
4
3
4
125 5
3
16 8
log3 81 4
1
log 2
5
32
1
log 1
3
64
4
1
log125 5
3
3
log16 8
4
(по
определению);
(по
определению);
8.
Найдите число xlog 5 x 2
2
x 5
25
log 3 x 1
1
1
xx
3
log 1 x 2
log 5 x 0
6
2
1 2
x
6
xx
36
6
3
51
x
x
0
9.
Найдите число xlog x 81 4
x 3
4
3 81
1
log x
2
16
log 1 x 2
1
log x 2
4
6
2
1 2
x
6
xx
36
6
2
1
1
x
x
44
1
2x
2 4
2
10.
Вычислите1
log 2 0,25 log 2 2
4
log 1 3
3
3 log 1 3 3
3
1
1
2
log 1 3
3
1
2
3
2
1
log 1 3 log 1
3
3
3
3
2
3
2
11.
Вычислите1
3 log 7 3 1 2
7
4
2 log 5 0,04 2 log5
100
1
2 log5
2 2 4
25
12.
Особые логарифмыДесятичные
логарифмы
(по основанию 10)
Натуральные
логарифмы
(по основанию е)
log10 a lg a
log e a ln a
13.
Пример2
lg 100 2, 10 100
1
lg 10 1, 10 10
lg 1 0, 10 1
0
lg 0,1 1, 10
1
0,1
lg 0,00001 5, 10
5
0,00001
14.
Свойства десятичных логарифмов:n
lg10 n
n
lg(0.1) n
n
lg b 10 lg b n
b
lg n lg b n
10
15.
Примерln e 1,
e e
2
2
1
ln e 2, e e
1
1
1
ln 1, e
e
e
2
log e e 1
ln e
1
2
3
ln e
1
3
16.
Вычислите устно значения логарифмов:log 3 9
log 32 2
log125 25
lg 0,01
1
log 2
8
1
log3
3
log 27 9
lg 0,001
log 4 16
log 9 3
log5 0,04
log 3 9
log 32 8
1
log 3
243
log81 27
lg 100
1
log 5
25
log 7 1
log 0 , 3 0 , 09
0,3
2
log 2 16
17.
Найдите число х.log4 x 3
log x 81 4
log 5 x 0
1
log x
2
16
log 5 x 2
log 1 x 1
1
log x 2
4
log 7 x 2
log 1 x 3
log3 x 1
log 1 x 3
6
7
2
log x 27 3
18.
Свойства логарифмов19.
ОСНОВНОЕЛОГАРИФМИЧЕСКОЕ
ТОЖДЕСТВО
a
log a b
b
( где b>0,a>0 и a ≠1)
20.
21.
Свойства логарифмовa
log a b
b , a 0, a 1, b 0
log a 1 0
log a a 1
22.
Вычислите:log 3 6
36
Воспользуемся свойством логарифмов:
a
log a b
b
log3 6
6
3
Решение
, т. е.
23.
Вычислите:log 1 1
0
3
Воспользуемся свойством логарифмов:
log a 1 0
log 1 1 0
3
Решение
, т. е.
24.
Вычислите:log 1
2
2
Воспользуемся свойством логарифмов:
log a a 1
log 2 2 1
Решение
, т. е.
25.
Вычислите:3 log 2 5
2 40
Воспользуемся свойством логарифмов:
a
2
3 log2 5
log a b
3
2 2
b
log2 5
8 5 40
Решение
, т. е.
26.
a)2lo g2 13
13
70
70
б ) log2 5 14
2
5
7
log7 13
13 1
в)
0,25
52
52 4
27.
Вычислите:a)4
б )3
log 4 7
2 log 3 11
в )10
3 lg 40
г ) 5 2
д)
5
log 5 6
48
log 2 7
а )7
б )99
в )25
г ) 35
д)0,125
28.
3 log2 93
2 2
log2 9
8 9 72
3 log4 32
3
log4 32
64 : 32 2
а)2
б )4
4 : 4
29.
Свойства логарифмов1
log
log 3 7
3 7
30.
1. Логарифм произведения равенсумме логарифмов множителей
31.
Свойства логарифмовlog a x log a y log a ( x y ),
а 0, х 0, y 0, а 1
т. е. логарифм произведения равен сумме
логарифмов сомножителей (взятых по тому
же основанию).
log6 2 + log6 3= log 6(2∙3) = log6
32.
Вычислите:log 6 122 log 6 3
Воспользуемся свойством логарифмов:
log a bc log a b log a c
, т. е.
log 6 12 log 6 3 log 6 12 6 log 6 36 2
Решение
33.
Вычислите:1. log18 2 + log18 9
2. log4 8 + log4 32
3. log32 2 + log32 2
4. lg 40 + lg 25
1) 1
2) 4
3) 0,2
4) 3
34.
2. Логарифм частного равенлогарифмов делимого без
логарифма делителя
35.
Свойства логарифмов36.
Вычислите:log 2 15– 1
log 2 30
Воспользуемся свойством логарифмов:
b
log a log a b log a c
c
, т. е.
15
1
log 2 15 log 2 30 log 2
log 2 1
30
2
Решение
37.
Вычислите:log 1 28 log 1 7
2
–2
2
Воспользуемся свойством логарифмов:
log a
b
log a b log a c
c
, т. е.
28
log 1 28 log 1 7 log 1
log 1 4 2
2
2
2 7
2
Решение
38.
Вычислите:log 2 4 6log 3 27
Воспользуемся свойством логарифмов:
loga a r r
2
, т. е.
3
log 2 4 log 3 27 log 2 2 log 3 3 2 3 6
Решение
выход
39.
3. Логарифм степени равенпроизведению показателя степени
на логарифм ее основания
40.
4. Логарифм, у которого основаниев степени
1
log a к x log а х
к
41.
Формула перехода к новомуоснованию:
log b x
log a x
log b a
Из этой формулы следует равенство:
1
log a b
log b a
42.
Вычислите:log7 25
log7 5
2
Воспользуемся свойством логарифмов:
log a b
log c b
log c a
log 7 25
log 5 25 2
log 7 5
Решение
, т. е.
43.
Свойства логарифмовlog 11 3 log 3 11 1
44.
а ) log 3 5 log 5 9 log 3 5 log 5 322 log 3 5 log 5 3 2
1 2
б )8
в )5
log2 5
4 log5 2
2
5
3 log2 5
log5 2 4
2
2
4
log2 53
3
5 125
1
1
4
0,0625
2
16
45.
Вычислите:1. log 2 7 log 7 8
2. log 5 11 log11 625
log3 2
3.81
4.5
2 log5 10
1) 3
2) 4
3) 16
4) 0,01
46.
Примерыln 216
ln 63
3 ln 6
3
4
a)
3 12
1
4
1
1
1
ln 6
4
ln
6
ln 6
4
4
n
a a
1
n
log a x n n log a x
log 0,3 8 log 0,3 8
log0,3 8
1
1
2
б)
1 : 1 2
log 0, 09 8 log 0,32 8 1 log 8 1
2
1
0 ,3
2
2
1
log a k x log a x
k
47.
Вычислите:lg 100
1. 6
lg 10
log 0, 2 125
2.
log 0, 2 5
log 5 81
3.
log 5 9
log 1 7
4.
2
log 1 49
2
1) 12
2) 3
3) 2
4) 0,5
48.
Преобразование логарифмических выражений49.
Преобразование логарифмическихвыражений









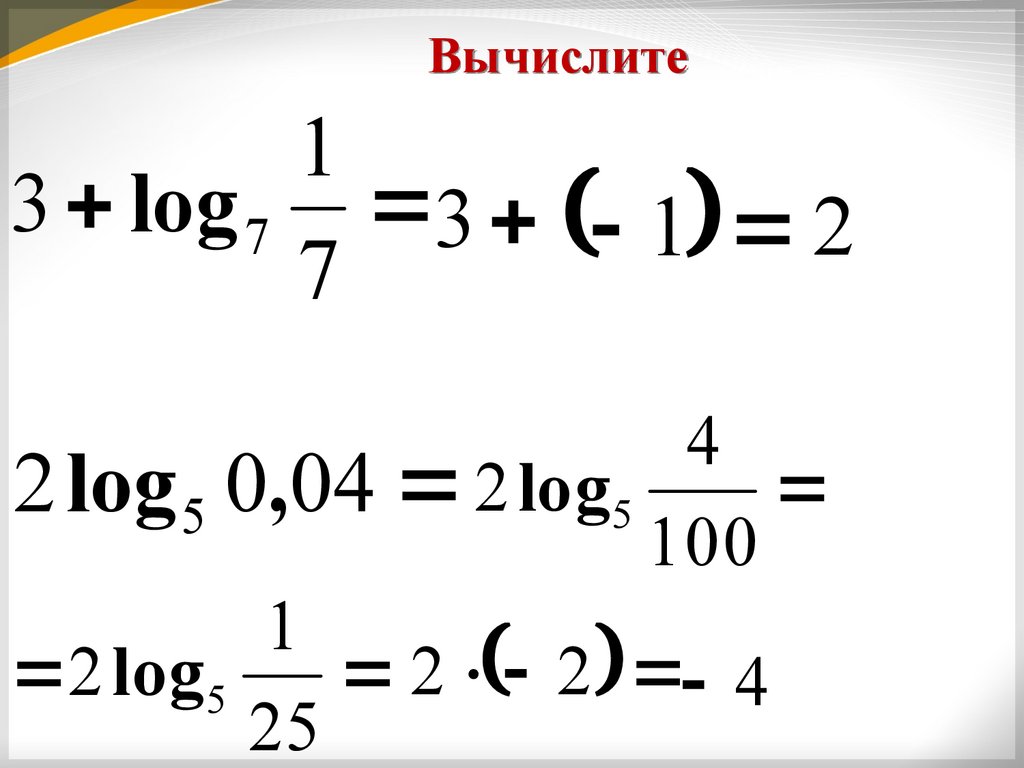







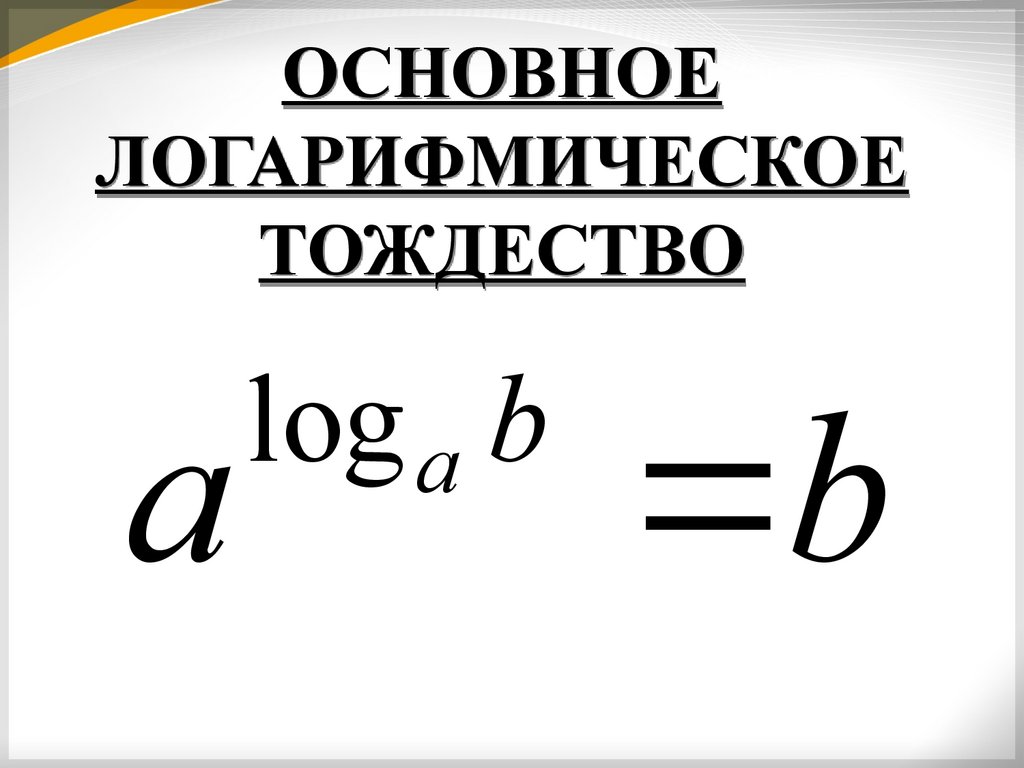






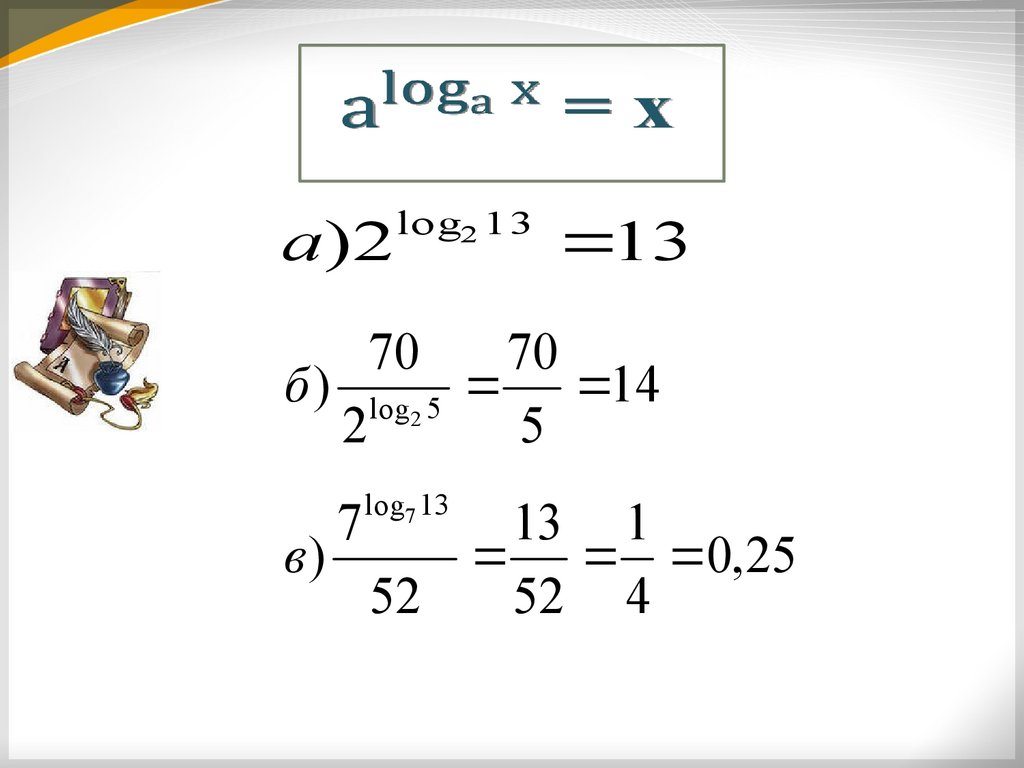

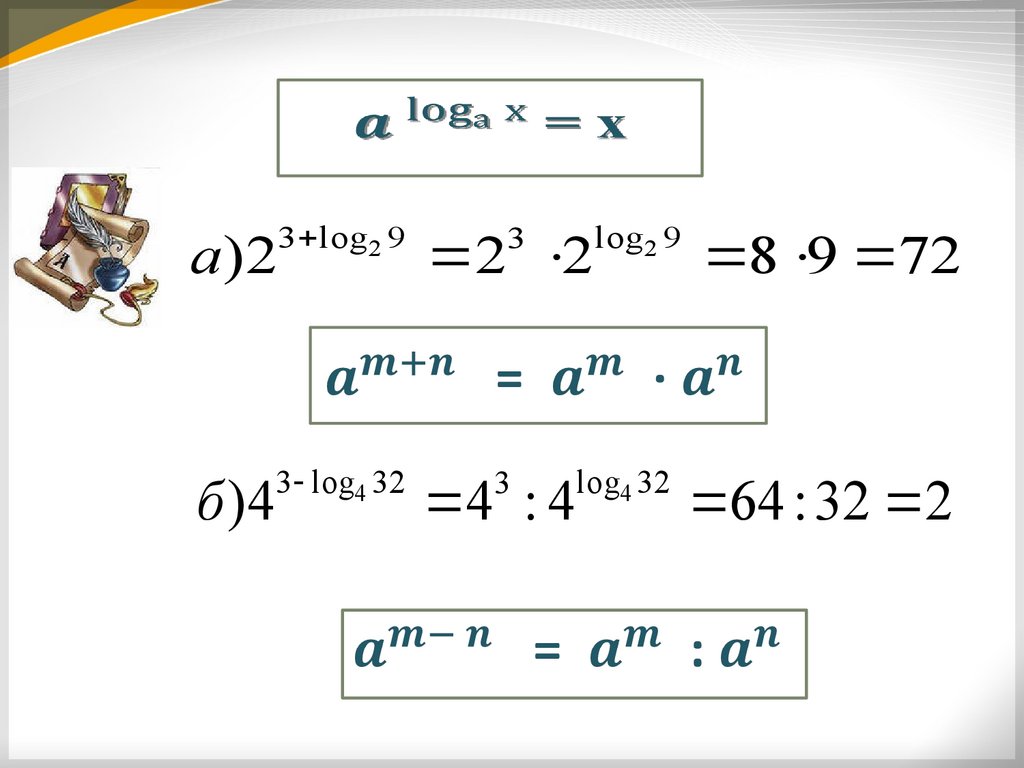















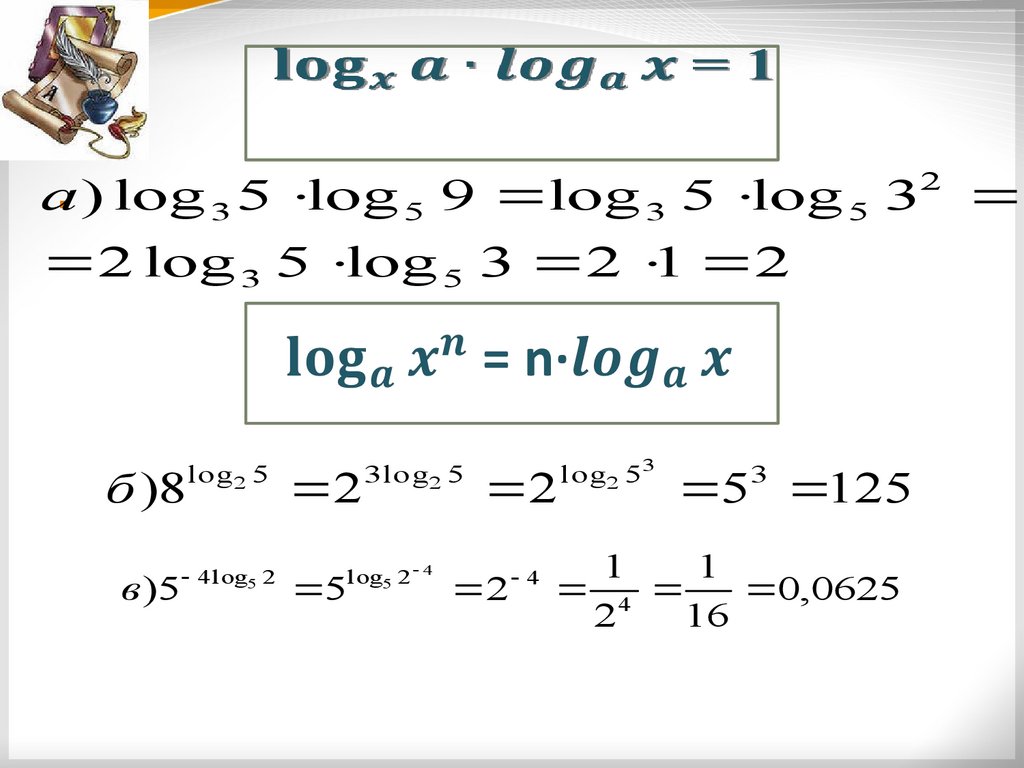





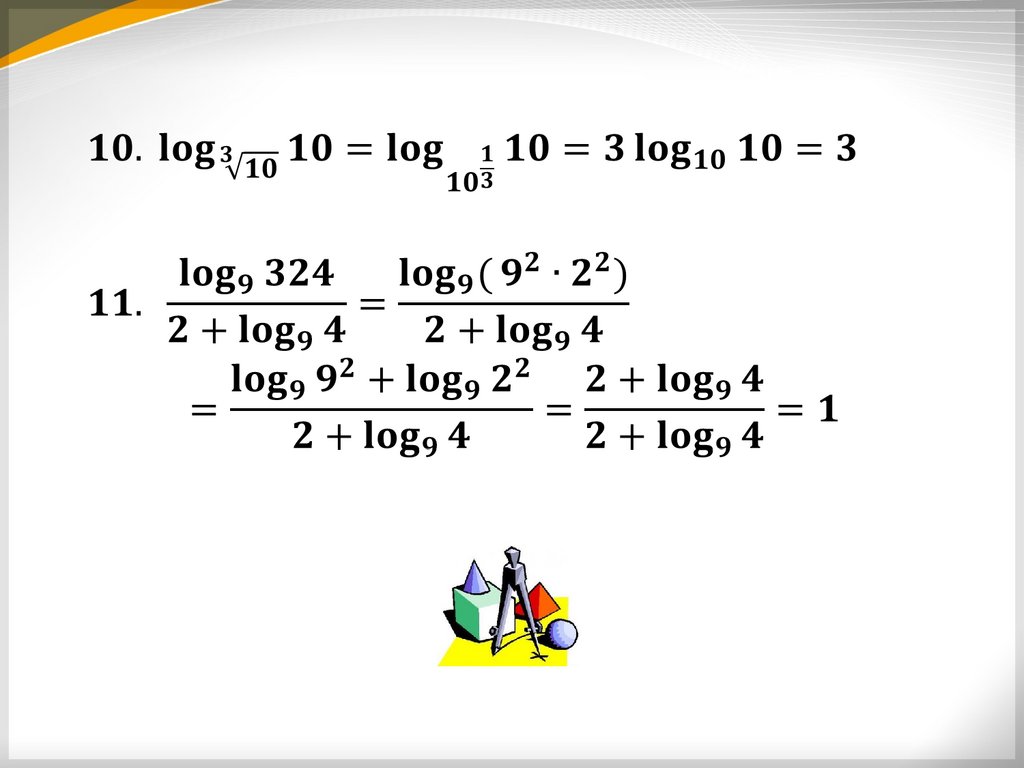


 mathematics
mathematics








