presentation (3)

1.

Использование интегралов в
высшей математике
Кафедра математического анализа

2.

Введение: Понятие интеграла
Интеграл — один из фундаментальных объектов математического анализа.
• Определённый интеграл — вычисление площади под кривой
• Неопределённый интеграл — нахождение первообразной функции
• Применение — физика, экономика, инженерия, статистика
• Основная теорема — связь между дифференцированием и интегрированием
\vspace{0.3cm}
Обозначение:

3.

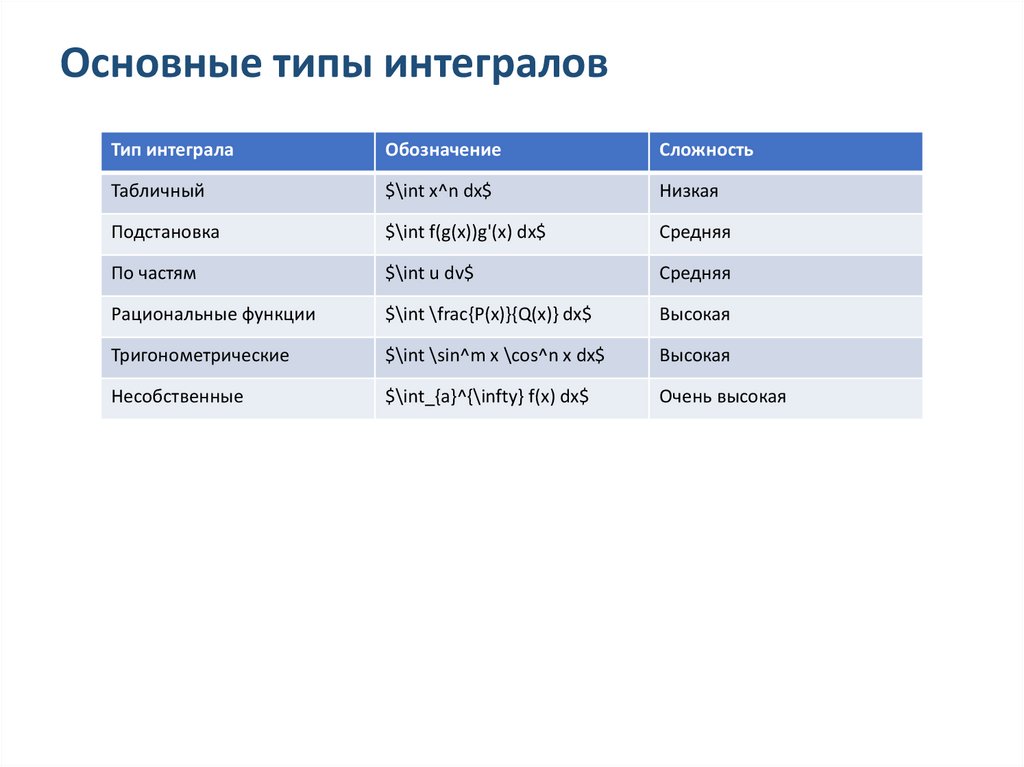
Основные типы интегралов
Тип интеграла
Обозначение
Сложность
Табличный
$\int x^n dx$
Низкая
Подстановка
$\int f(g(x))g'(x) dx$
Средняя
По частям
$\int u dv$
Средняя
Рациональные функции
$\int \frac{P(x)}{Q(x)} dx$
Высокая
Тригонометрические
$\int \sin^m x \cos^n x dx$
Высокая
Несобственные
$\int_{a}^{\infty} f(x) dx$
Очень высокая

4.

Фундаментальные формулы интегрирования
Табличные интегралы:
Основная теорема исчисления:
где [F'(x) = f(x)] — первообразная функции [f(x)].

5.

Метод интегрирования по частям
Формула:
Пример: Вычислим [\int x e^x dx]
Полагаем: [u = x], [dv = e^x dx]
Тогда: [du = dx], [v = e^x]
Применение: произведения многочленов, экспонент, тригонометрических и
логарифмических функций.

6.

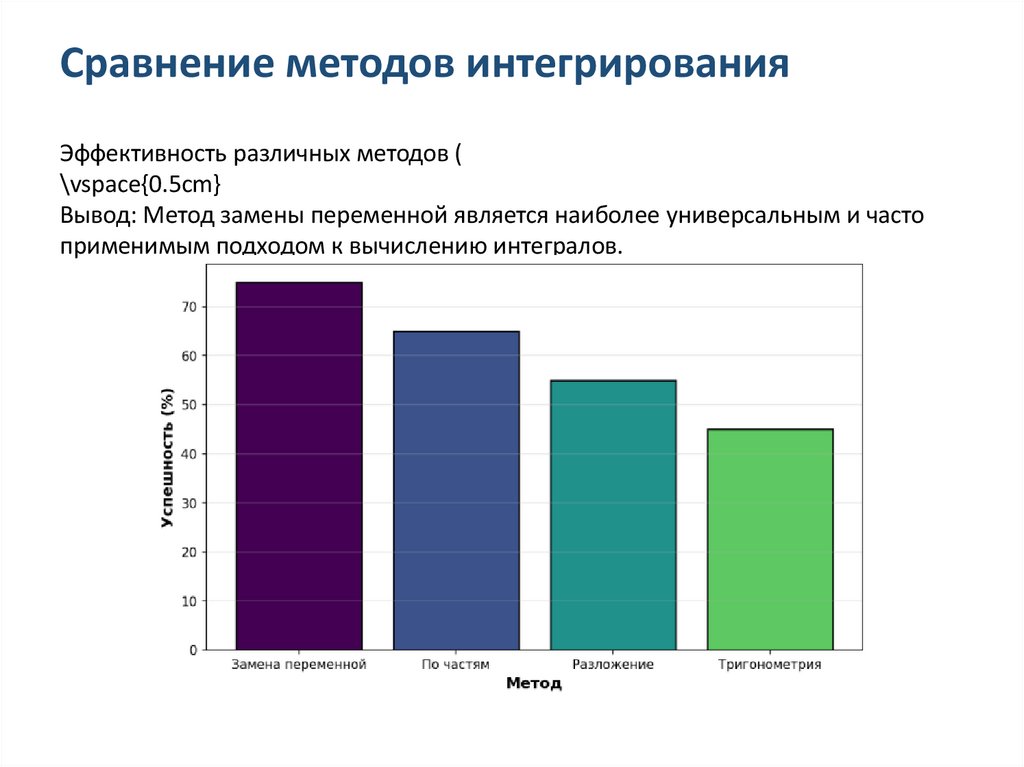
Сравнение методов интегрирования
Эффективность различных методов (
\vspace{0.5cm}
Вывод: Метод замены переменной является наиболее универсальным и часто
применимым подходом к вычислению интегралов.

7.

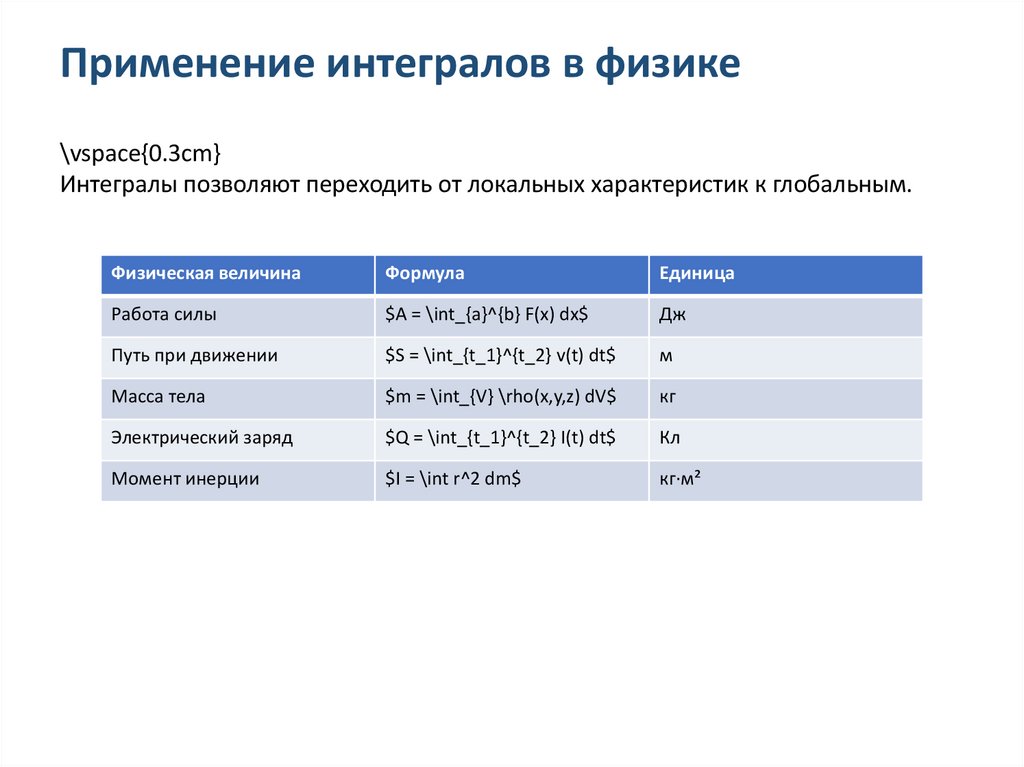
Применение интегралов в физике
\vspace{0.3cm}
Интегралы позволяют переходить от локальных характеристик к глобальным.
Физическая величина
Формула
Единица
Работа силы
$A = \int_{a}^{b} F(x) dx$
Дж
Путь при движении
$S = \int_{t_1}^{t_2} v(t) dt$
м
Масса тела
$m = \int_{V} \rho(x,y,z) dV$
кг
Электрический заряд
$Q = \int_{t_1}^{t_2} I(t) dt$
Кл
Момент инерции
$I = \int r^2 dm$
кг·м²

8.

Несобственные интегралы
Интегралы с бесконечными пределами:
Интегралы от неограниченных функций:
Гауссов интеграл:

9.

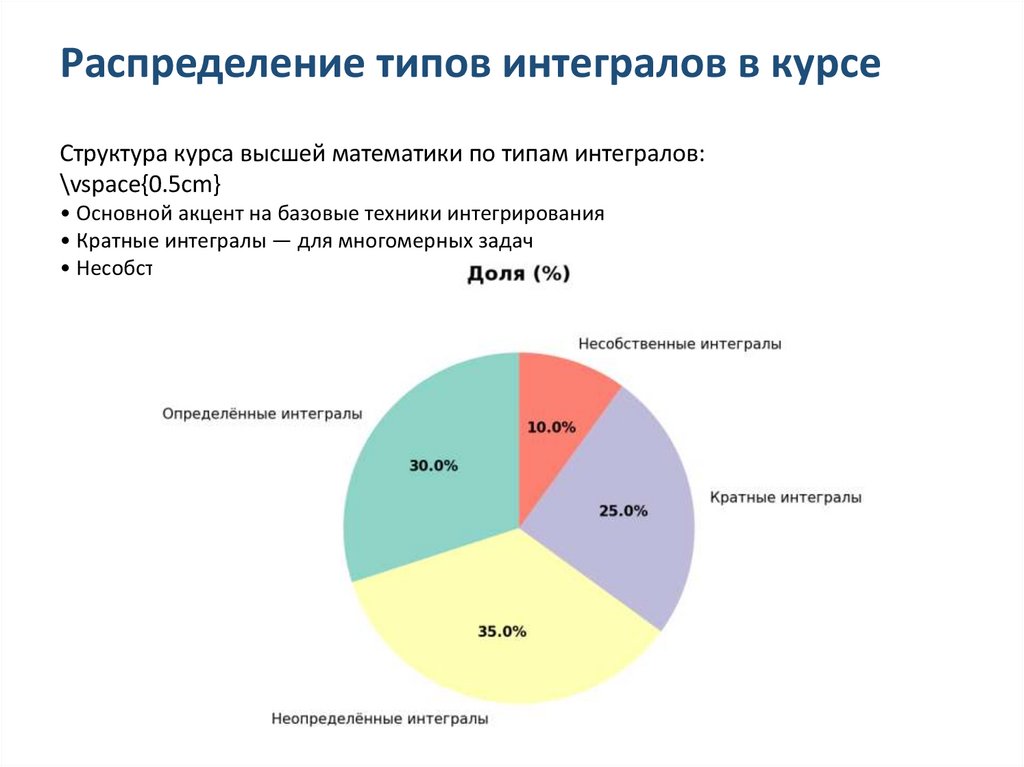
Распределение типов интегралов в курсе
Структура курса высшей математики по типам интегралов:
\vspace{0.5cm}
• Основной акцент на базовые техники интегрирования
• Кратные интегралы — для многомерных задач
• Несобственные интегралы — для продвинутого уровня