3.2. Метод контурных токов (1)

1. ПОСТОЯННЫЙ ТОК   Методы исследования сложных цепей 3.2. Метод контурных токов

ПОСТОЯННЫЙ ТОК
Методы исследования сложных
цепей
3.2. Метод контурных токов

2.

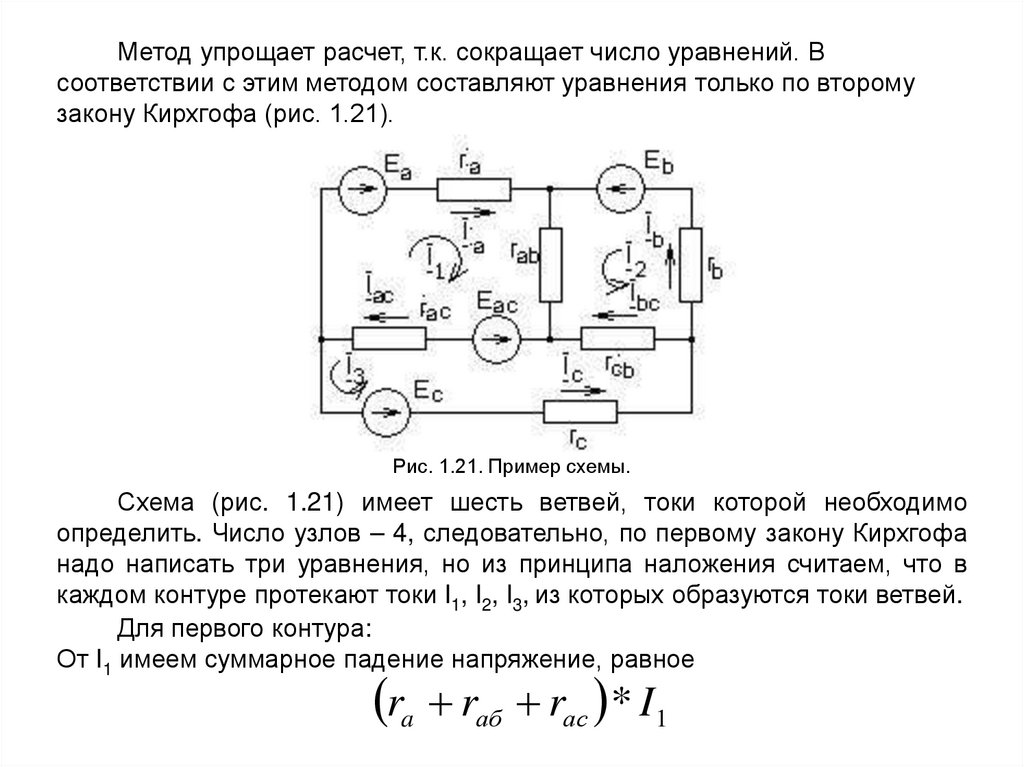
Метод упрощает расчет, т.к. сокращает число уравнений. В
соответствии с этим методом составляют уравнения только по второму
закону Кирхгофа (рис. 1.21).
Рис. 1.21. Пример схемы.
Схема (рис. 1.21) имеет шесть ветвей, токи которой необходимо
определить. Число узлов – 4, следовательно, по первому закону Кирхгофа
надо написать три уравнения, но из принципа наложения считаем, что в
каждом контуре протекают токи I1, I2, I3, из которых образуются токи ветвей.
Для первого контура:
От I1 имеем суммарное падение напряжение, равное
ra rаб rас * I1

3.

по rab проходит ток I2 в направлении обхода контура, создает падение
напряжения U=rabI2;
по raс проходит ток I3 в направлении обхода контура, создает падение
напряжения U=raсI3
Имеем для первого контура:
ra rаб rас * I1 rаб I 2 rас I 3 Ea Eac
Аналогично составляются для второго и третьего контуров:
ra ràá ràñ * I 2 ràá I1 ráñI 3 Eá
ra rаб rас * I 3 rас I1 rбс I 2 Eс Eac
Условимся сумму всех сопротивлений любого контура называться
собственным сопротивлением этого контура. Тогда
r11 rа rаб rас ; r22 rб rаб rбс ; r33 rс rас rбс ;

4.

Сопротивление резисторов, которые одновременно входят в состав
двух контуров, будем называть взаимными. И считать их положительными,
если направления контурных токов в них совпадают, и отрицательными,
когда направления этих токов противоположны:
r12 r21 rаб
– направления I1 и I2 в rab совпадают;
r23 r32 rбс – токи I2 и I3 в rbс противоположны по направлению;
r13 r31 rас
– токи I1 и I3 в raс направления одинаковы.
Алгебраическая сумма всех ЭДС, действующих в любом контуре,
называется контурной ЭДС.
E1 Eа Eас ; E2 Eб ; E3 Eс Eас ;
Имеем:
I1r11 I 2 r12 I 3 r13 E1
I1r21 I 2 r22 I 3 r23 E2
I1r31 I 2 r32 I 3 r33 E3

5.

Для сложной цепи из n контуров:
I 1 r11 I 2 r12 I 3 r13 ... I k r1k ... I n r1n E1
I r I r I r ... I r ... I r E
3 23
k 2k
n 2n
2
1 21 2 22
...
...
I r I r I r ... I r ... I r E
2 k2
3 k3
k kk
n kn
k
1 k1
...
I 1 rn1 I 2 rn 2 I 3 rn 3 ... I k rnk ... I n rnn E n
(1.32)
Решая эту систему определяем:
Ik
1k
E1 2 k E2 ... kk Ek ... nk En
(1.33)
где ∆ – главный определитель матрицы для системы уравнений (1.32)
∆mk – алгебраическое дополнение, получаемое при вычеркивании в
главном определителе m-й строки и k-го столбца и умножении полученного
определителя на (-1)m+k

6.

Ток в каком-либо резисторе равен алгебраической сумме контурных
токов. При этом положительным считается такой контурный ток, который в
данном резисторе совпадает по направлению с результирующим током,
следовательно
I a I1 ; I aб I1 I 2
и т.д.
Определитель системы уравнений (1.32)
r11r12 ...r1k ...r1n
r21r22 ...r2 k ...r2 n
...
rk1 rk 2 ...rkk ...rkn
(1.34)
...
rn1 rn 2 ...rnk ...rnn
mk k 1,2...n – алгебраическое дополнение, получаемое из
а
определителя ∆ посредством вычеркивания m-й строки и k-го столбца.
Следующая тема