Similar presentations:
Разложение функций в степенные ряды. Ряды Тейлора и Маклорена
1. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена
Разложение функций вст епенные ряды.
Ряды Тейлора и Маклорена
Пусть функция f ( x ) имеет производные до (n 1)
порядка включительно. Известна формула
Тейлора:
f x 0
f x 0
x x 0
x x 0 2
f x f x 0
1!
2!
f n x 0
x x 0 n R n x ,
n!
R n x остаток,
который
вычисляется
по
формуле
f ( n 1) (c)
R n x
( x x 0 ) n 1,
(n 1)!
где, c x 0 ( x x 0 ) , 0 1, т.е. с ( х 0 ; х ) .
f ( x ) Sn ( x ) R n ( x ) .
2.
Если функция f ( x ) имеет производные любыхпорядков, то получаем ряд Тейлора для f ( x ) :
f x 0
x x 0
f x f x 0
1!
f x 0
f x 0
2
x x 0
x x 0 3
2!
3!
или
f (n ) (x
f (x)
n 0
n!
0)
(x x 0 )n .
3.
Если х 0 0, то получим ряд Маклорена:f 0
f 0 2 f (0) 3
f x f 0
х
х
x
1!
2!
3!
или
f ( n ) (0)
n
f (x)
х .
n!
n 0
4.
Теорема 8.1. Для того, чтобы рядТейлора функции f ( x ) сходился к f ( x )
в точке х необходимо и достаточно,
чтобы в этой точке lim R n ( x ) 0.
n
Теорема 8.2. (достаточное условие
сходимости ряда к f ( x ) )
Если модули всех производных f ( x )
ограничены в окрестности точки х 0
одним и тем же числом M 0
f ( n ) ( x ) M , то для всех х из этой
окрестности ряд Тейлора функции f ( x )
сходится к функции f ( x ) .
5.
Разложение некоторых функций вряд Маклорена
Схема разложения функции f ( x ) в
ряд Маклорена:
1). вычисляются значения функции
и ее производных при х 0 , т.е. f (0) ,
(n )
f (0) , f (0) , f (0) , , f (0) ,
6.
2).записывается ряд
f ( n ) ( 0)
n
х ,
n!
находится его радиус сходимости по
формулам
(7.1)
или
(7.2):
an
1
R lim
, R lim
, затем
n a n 1
n n a n
находится интервал сходимости
3). находится интервал, в котором
lim R n ( x ) 0 или f (n ) ( x ) M , тогда в
n 0
n
этом интервале сумма ряда и f ( x )
совпадают.
7.
Таблица разложения функций в рядМаклорена
2
n
xn
x
x
x
ex 1
1! 2!
n!
n 0 n !
х ( ; )
2n 1
x3 x5 x 7
x
sin x x
1 n 1
2n 1 !
3! 5! 7!
х ( ; )
2n 2
x2 x4 x6
x
cos x 1
1 n 1
2n 2 !
2 ! 4! 6!
х ( ; )
8.
(1 х )m 1m
m m 1 2 m m 1 m 2 3
x
x
x
1!
2!
3!
m m 1 m n 1 n
x
n!
при m 0; x 1;1
при m ( 1;0) x 1;1
при m ; 1 х ( 1;1)
1
2
3
n
n
1 x x x 1 x 1 n x n
1 x
n 0
x ( 1;1)
9.
11 x x 2 x 3 x n x n x ( 1;1)
1 x
n 0
1 x3 1 3 x5 1 3 5 x 7
arcsin x x
2 3 2 4 5 2 4 6 7
x 1;1
1 3 5 2n 1 x 2n 1
2 4 6 2n 2n 1
n 1
x 2 x3 x 4
x
ln 1 x x
1 n
2
3
4
n 1
x 1;1
10.
32n 1
5
x
x
x
n
arctgx x 1
3
5
2n 1
x 1;1
2
4
3
5
6
2n
x
x
x
x
chx 1
2! 4! 6!
(2n )!
х ( ; )
2n 1
x
x
x
shx x
3! 5!
(2n 1)!
х ( ; )
11.
9. Применениястепенных рядов
f (x)
Если
функцию
можно разложить в степенной
ряд
a 0 a1x a 2x 2 ,
то приближенное значение
функции равно частичной
сумме Sn ( x )
Sn ( x ) a 0 a1x a 2x 2 a n x n
12.
Точность вычисления увеличивается с ростом числаслагаемых, т.е. с ростом n. Погрешность замены f ( x )
на Sn ( x ) равна остатку ряда
R n ( x ) a n 1x n 1 a n 2 x n 2 .
Для знакочередующихся рядов по теореме Лейбница
R n ( x ) a n 1x n 1 .
Для знакоположительных и знакопеременных рядов
подбирают мажоранту, т.е. числовой сходящийся ряд,
у которого легко можно найти сумму. Например,
убывающая геометрическая прогрессия, сумма
b
которой S
.
1 q
13.
Пример 9.1. Вычислить Cos100 с точностью до 10 4 .Решение.
Воспользуемся готовым разложением
функции f ( x ) Cos x в ряд Маклорена
2n 2
x2 x4 x6
x
cos x 1
1 n 1
.
2n 2 !
2 ! 4! 6!
100
, то
Т.к. 10
1800 18
0
2
4
6
8
Cos100 1 18 18 18 18
2!
4!
6!
8!
1
2
4
6
182 2 184 1 2 3 4 186 1 2 3 4 5 6
1 0,00484 0,000039
14.
Эточисловой
знакочередующийся ряд, причем
0,00484 10 4 , а 0.000039 10 4 .
Следовательно
остаток
ряда
R 3 0.000039 0.000039 10 4 ,
т.е. меньше заданной точности и
им можно пренебречь.
Cos100 1 0.00484 0.9948.







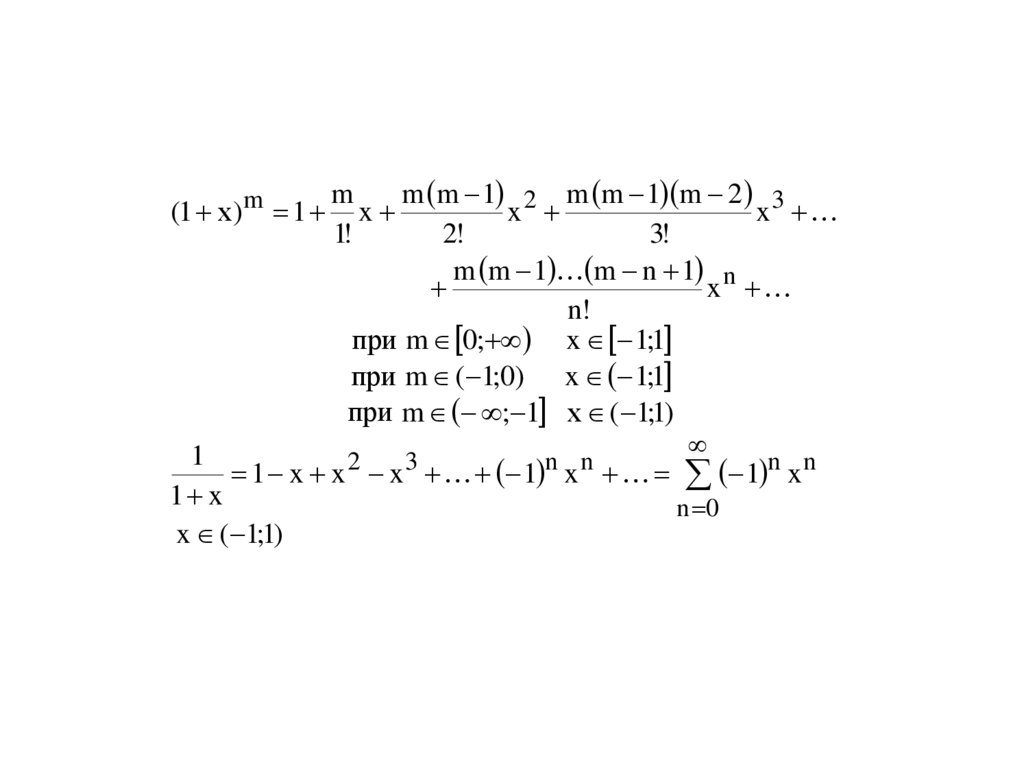
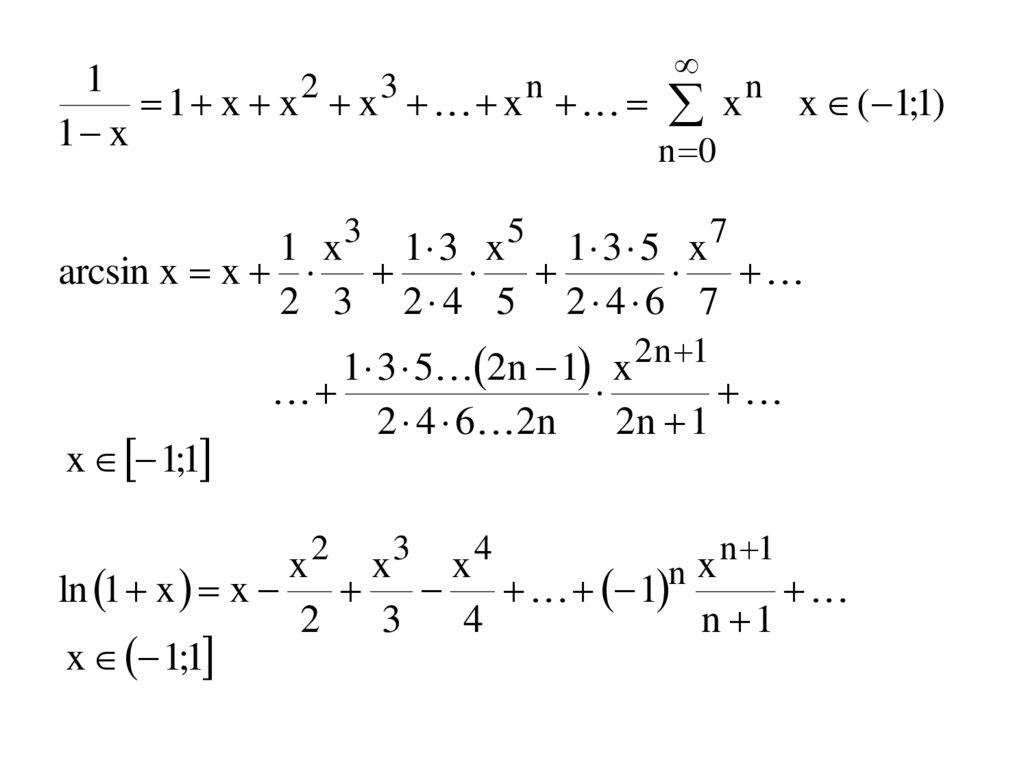
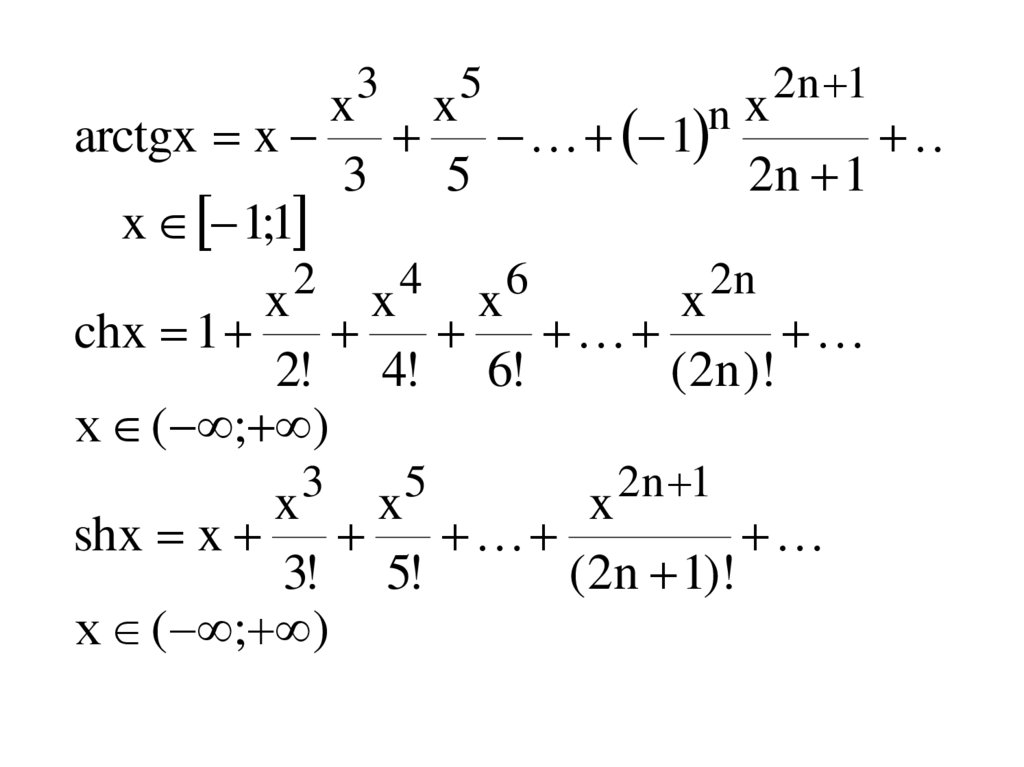




 mathematics
mathematics