Similar presentations:
Расположение элементарных функций в ряд Маклорена. (Тема 14.4)
1.
1y e
x
2.
f ( x) f ( x) f ( x) ... f( n)
( x) e
x
f (0) f (0) f (0) ... f (0) e 1
( n)
Подставляем найденные
Маклорена:
величины
0
в
ряд
3.
23
n
n
x
x
x
x
e 1 x
...
...
2! 3!
n!
n 0 n!
x
Область сходимости ряда
( ; )
4.
2y sin x
5.
f ( x) sin xf ( x) cos x
f ( 0) 0
f ( x) sin x
f (0) 0
f ( x) cos x
f (0) 1
f ( x) sin x
.....
( 4)
f (0) 1
f
(0) 0
.....
( 4)
6.
Производные четного порядка все равны нулю:f
(2n)
(0) 0
Производные нечетного порядка равны:
f
где
( 2 n 1)
(0) ( 1)
n
n 0,1,2...
Подставляем найденные
Маклорена:
величины
в
ряд
7.
2 n 1x3 x5
x
n
sin x x ... ( 1)
...
3! 5!
(2n 1)!
2 n 1
x
( 1)
(2n 1)!
n 0
n
Область сходимости ряда
( ; )
8.
3y cos x
9.
f ( x) cos xf ( 0) 1
f ( x) sin x
f (0) 0
f ( x) cos x
f (0) 1
f ( x) sin x
f (0) 0
f
( 4)
( x) cos x
.....
f
(0) 1
.....
( 4)
10.
Производные нечетного порядка все равны нулю:f
( 2 n 1)
(0) 0
Производные четного порядка равны:
f
где
(2n)
(0) ( 1)
n
n 0,1,2...
Подставляем найденные
Маклорена:
величины
в
ряд
11.
2nx2 x4
x
n
cos x 1
... ( 1)
...
2! 4!
(2n)!
2n
x
( 1)
(2n)!
n 0
n
Область сходимости ряда
( ; )
12.
4y (1 x)
m
13.
f ( x) (1 x)m
m 1
f ( x) m (1 x)
f ( x) m (m 1) (1 x)
m 2
f ( x) m (m 1) (m 2) (1 x)
.....
f
( n)
m 3
( x) m (m 1) (m 2) ... (m n 1)(1 x)
Следовательно:
m n
14.
f ( 0) 1f (0) m
f (0) m (m 1)
f (0) m (m 1) (m 2)
.....
f
( n)
(0) m (m 1) (m 2) ... (m n 1)
Подставляем найденные
Маклорена:
величины
в
ряд
15.
m (m 1) 2 m (m 1) (m 2) 3(1 x) 1 m x
x
x
2!
3!
m (m 1) (m 2) ... (m n 1) n
...
x ...
n!
m
Интервал сходимости ряда
( 1;1)
16.
Этот ряд называется биномиальным.Если число m – целое и положительное, то
биномиальный
ряд
представляет
собой
формулу бинома Ньютона, т.к. при
n=m+1
m-n+1=0
следовательно n-ый и все последующие члены
ряда будут равны нулю, т.е. ряд обрывается и
вместо бесконечного разложения получается
конечная сумма.
17.
5y ln( 1 x)
18.
f ( x) ln( 1 x)f ( 0) 0
1
f ( x)
1 x
1
f ( x)
2
(1 x)
2
f ( x)
3
(1 x)
6
( 4)
f ( x)
4
(1 x)
.....
f (0) 1
f (0) 1
f (0) 2
f
(0) 6
.....
( 4)
n
(
1
)
(n)
f (0)
n 1
19.
n 1x 2 x3
x
ln( 1 x) x
... ( 1) n
...
2
3
n 1
n 1
n x
( 1)
n 1
n 0
Область сходимости ряда
( 1;1]
20.
Разложить в ряд функциюx2
1 e
y
2
x
21.
23
n
x
x
x
e 1 x
...
...
2!
3!
n!
x
e
x
4
2n
x
n x
1 x
... ( 1)
...
2!
n!
2
2
1 e
x
2
x2
1 e
x2
4
2n
x
n 1 x
x
... ( 1)
...
2!
n!
2
2n 2
x2
x
1
... ( 1) n 1
...
2!
n!



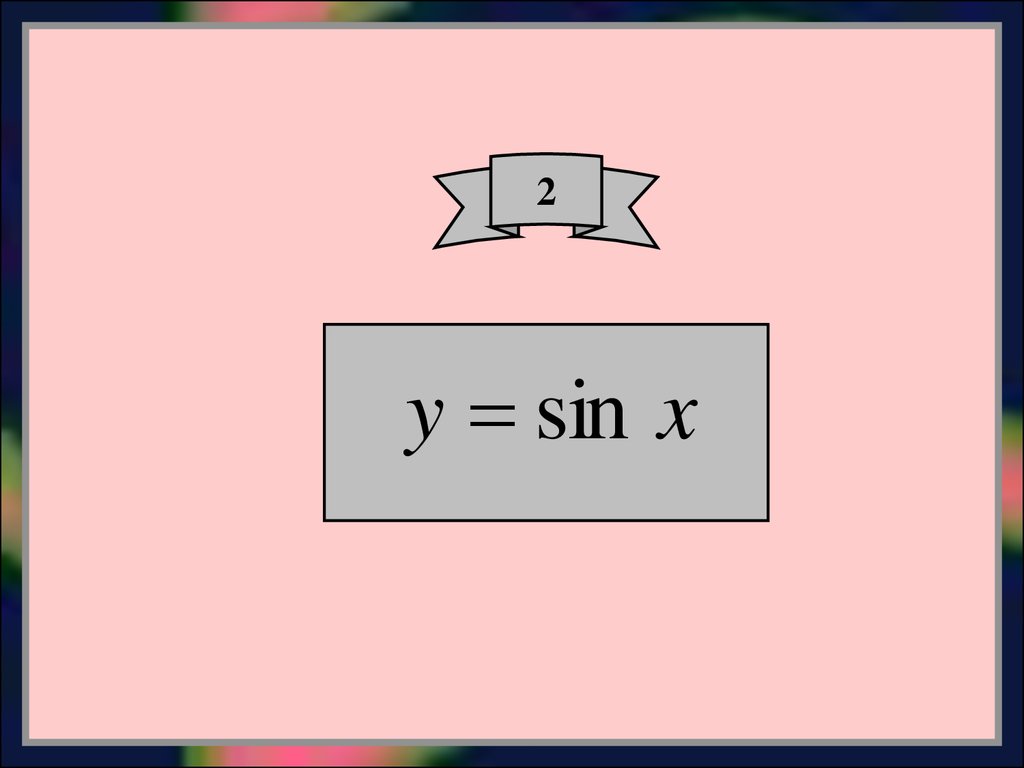
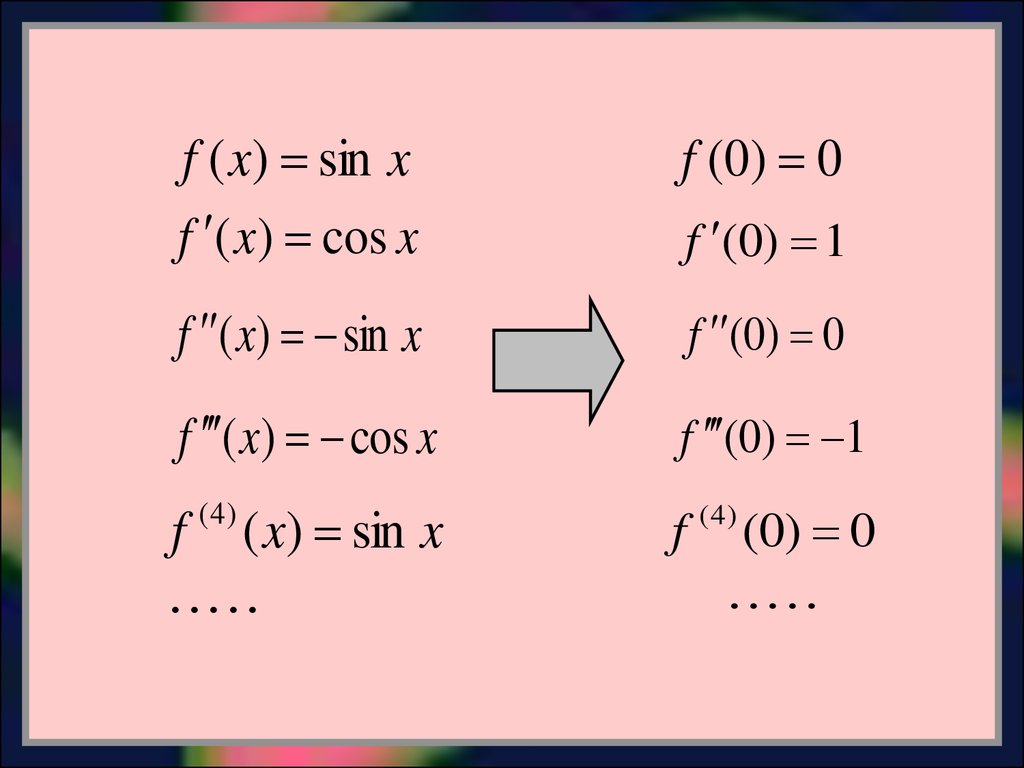


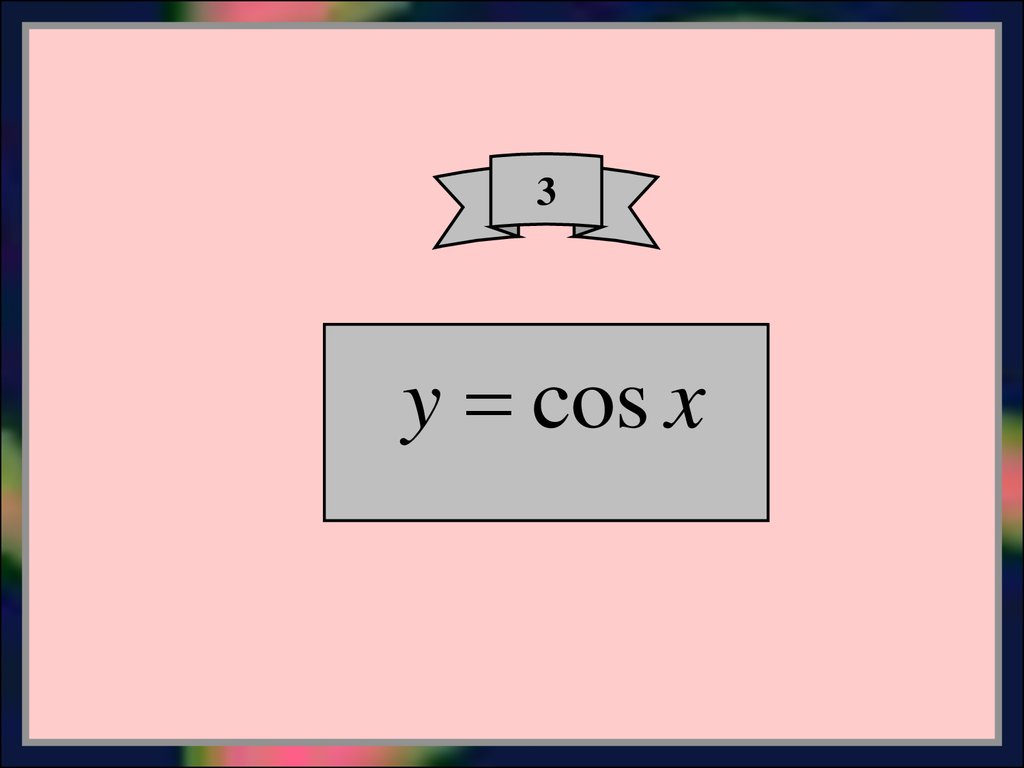
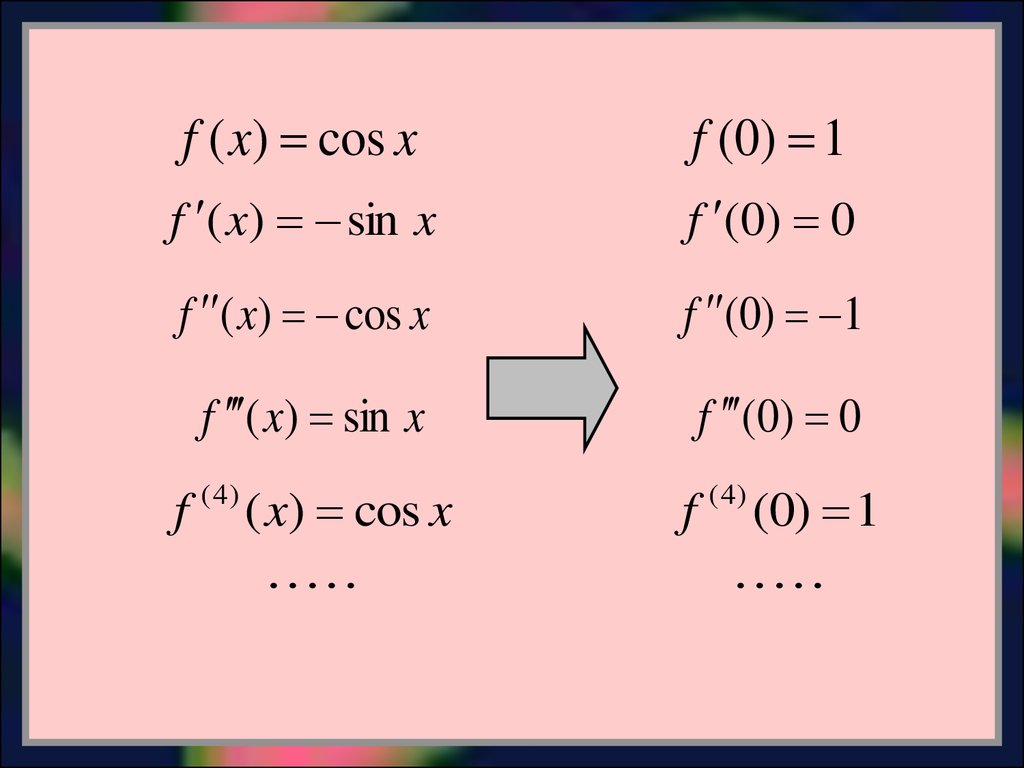


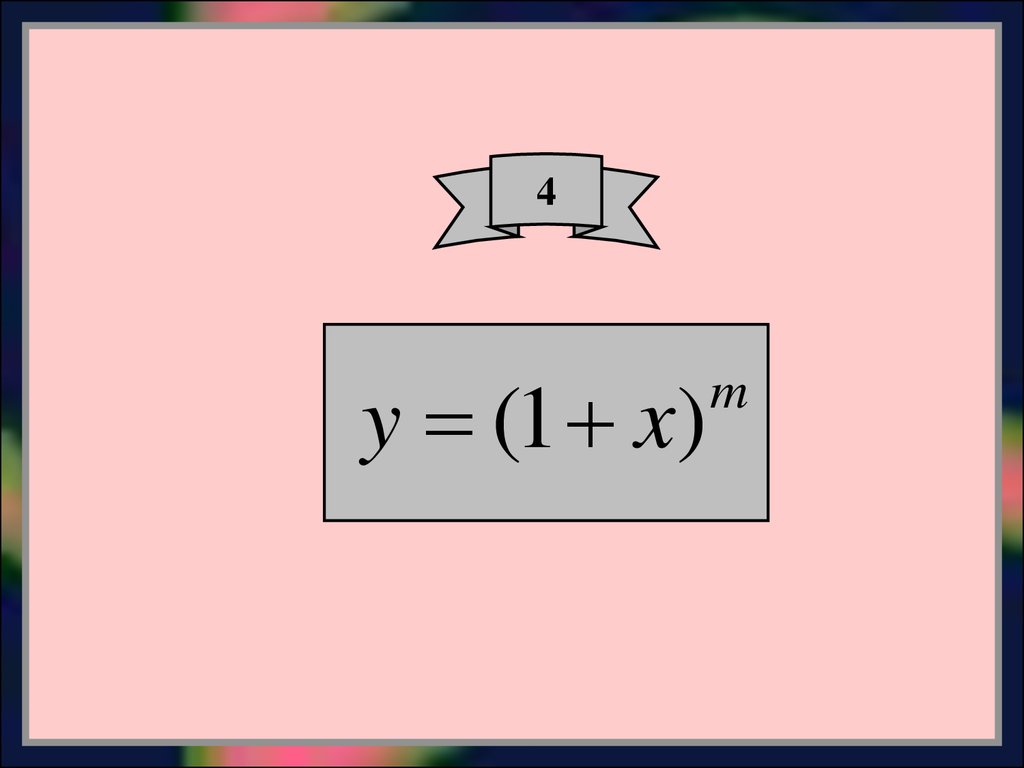




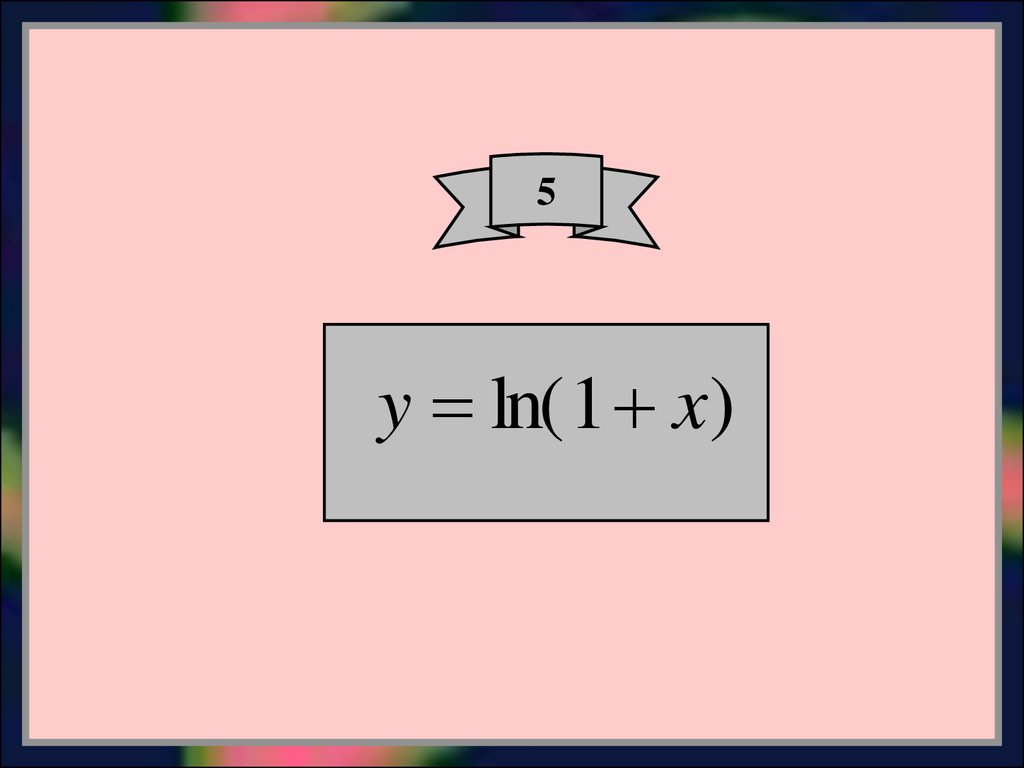
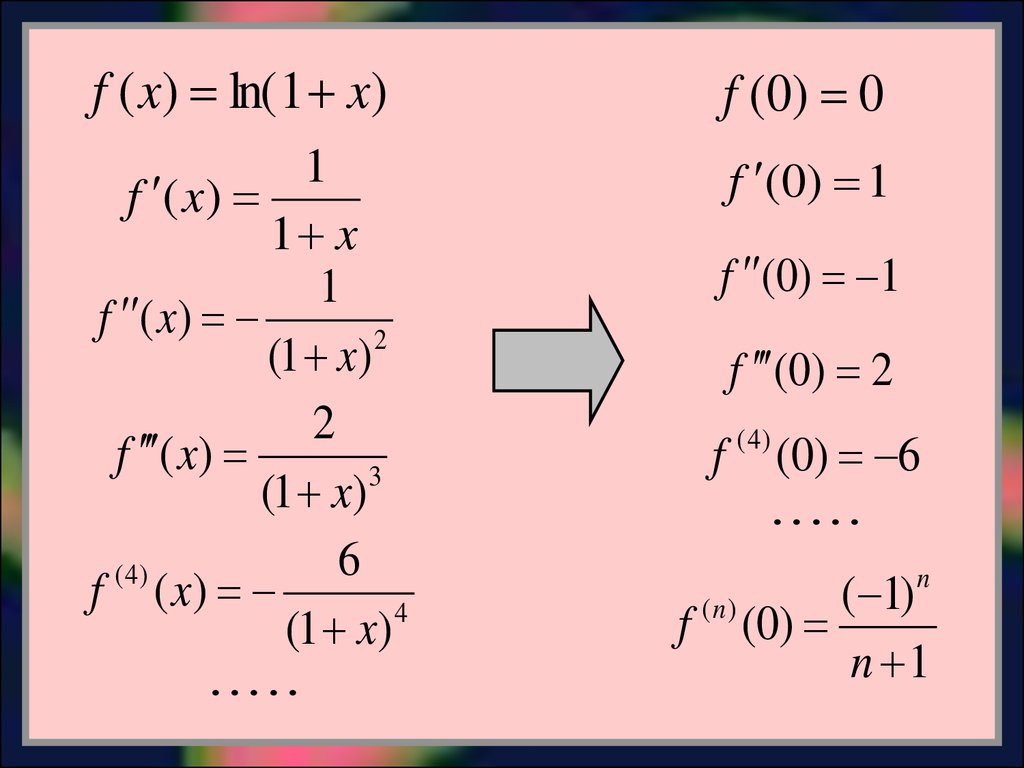


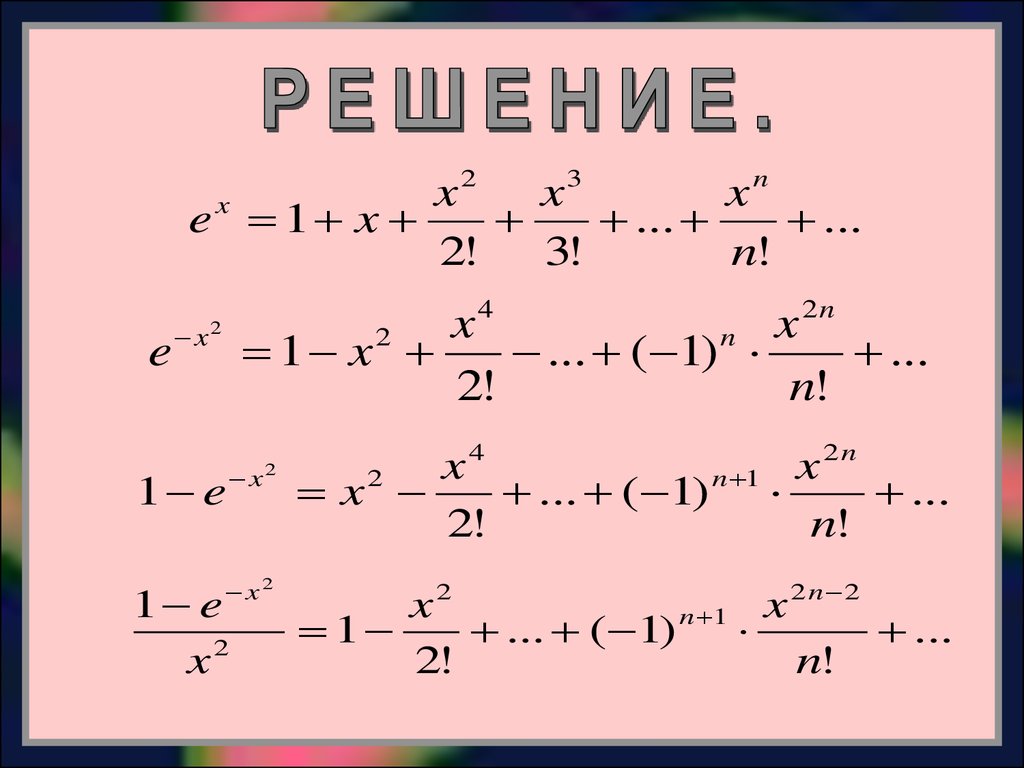
 mathematics
mathematics








