Similar presentations:
Производные элементарных функций
1.
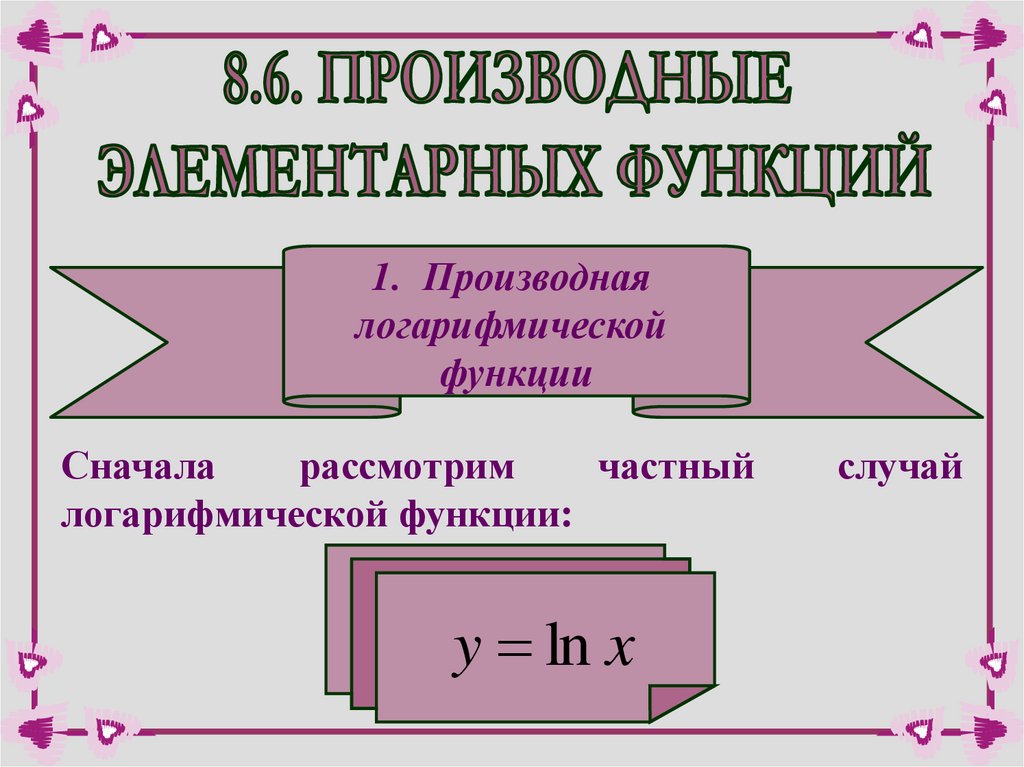
1. Производнаялогарифмической
функции
Сначала
рассмотрим
частный
логарифмической функции:
y ln x
случай
2.
Используем схему нахождения производной:Дадим аргументу х приращение Δх и найдем
значение функции y+Δy:
y y ln( x x)
Находим приращение функции
y ln( x x) ln x
По свойству логарифма:
x x
x
ln
ln 1
x
x
3.
Составляем отношениеy 1 x
ln 1
x x
x
Находим предел этого отношения:
y
1 x
y lim
lim
ln 1
x 0 x
x 0 x
x
Сделаем замену:
x
y ; x xy
x
4.
Тогда1
1
1
1
1
ln 1 y y
lim
ln 1 y lim ln 1 y y lim
y 0 x
y 0 xy
x y 0
В силу непрерывности логарифмической
функции меняем местами знаки логарифма и
предела:
1
1
1
1
ln lim 1 y y ln e
x y 0
x
x
e
1
5.
1(ln x)
x
Для сложной функции:
1
(ln u ) u
u
6.
ПРИМЕР.y 3ln x
2
1
6
y (3 ln x ) 3 2 2 x
x
x
2
7.
Найдем производную для общего случаялогарифмической функции:
y log a x
8.
По свойству логарифмаln x
log a x
ln a
Тогда
ln x
1
1
y (log a x)
(ln x)
ln a
x ln a
ln a
1
x
Отсюда окончательно имеем
9.
1(log a x)
x ln a
Для сложной функции:
1
(log a u )
u
u ln a
10.
ПРИМЕР.y log5 ( x 3x)
2
1
1
y (log 5 ( x 3x)) 2
(2 x 3)
x 3x ln 5
2
11.
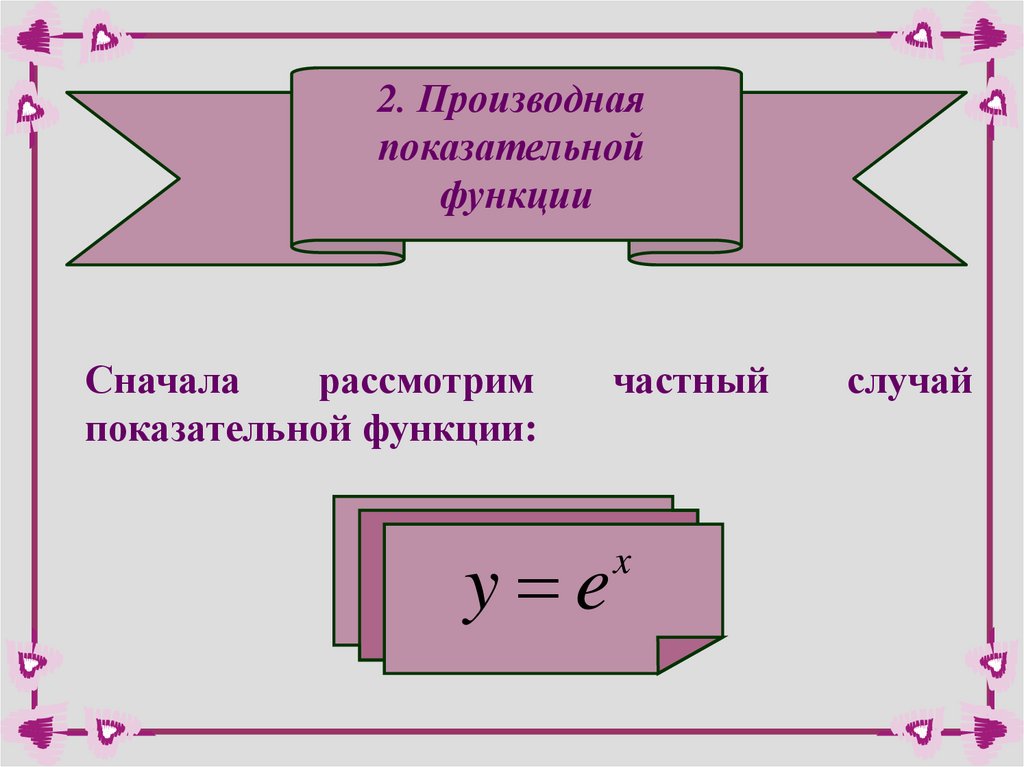
2. Производнаяпоказательной
функции
Сначала
рассмотрим
показательной функции:
y e
частный
x
случай
12.
Логарифмируемоснованию e:
обе
части
равенства
ln y ln e x ln e x
x
Дифференцируем обе части равенства по х:
1
y 1
(ln y ) x
y
Отсюда выражаем искомую производную:
y y
Т.к.
y e
x
то окончательно получаем:
y e
x
по
13.
(e ) ex
x
Для сложной функции:
(e ) e u
u
u
14.
Криваяy e
x
(экспонента) обладает свойством: в каждой
точке х ордината у равна угловому
коэффициенту касательной к кривой в этой
точке:
e tg
x
15.
ПРИМЕР.y x e
5x
y ( x e ) e x 5 e e (1 5x)
5x
5x
5x
5x
16.
Найдем производную для общего случаяпоказательной функции:
y a
x
17.
y (a )x
Т.к.
a e
(e
e
ln a x
)
x ln a
a
x
ln a
(e
x ln a
)
ln a a ln a
x
18.
(a ) a ln ax
x
Для сложной функции:
(a ) a ln a u
u
u
19.
ПРИМЕР.y 7
y (7
3 x3 x
7
) 7
3 x3 x
3 x3 x
3 x3 x
ln 7 3x x
3
ln 7 (9 x 1)
2
20.
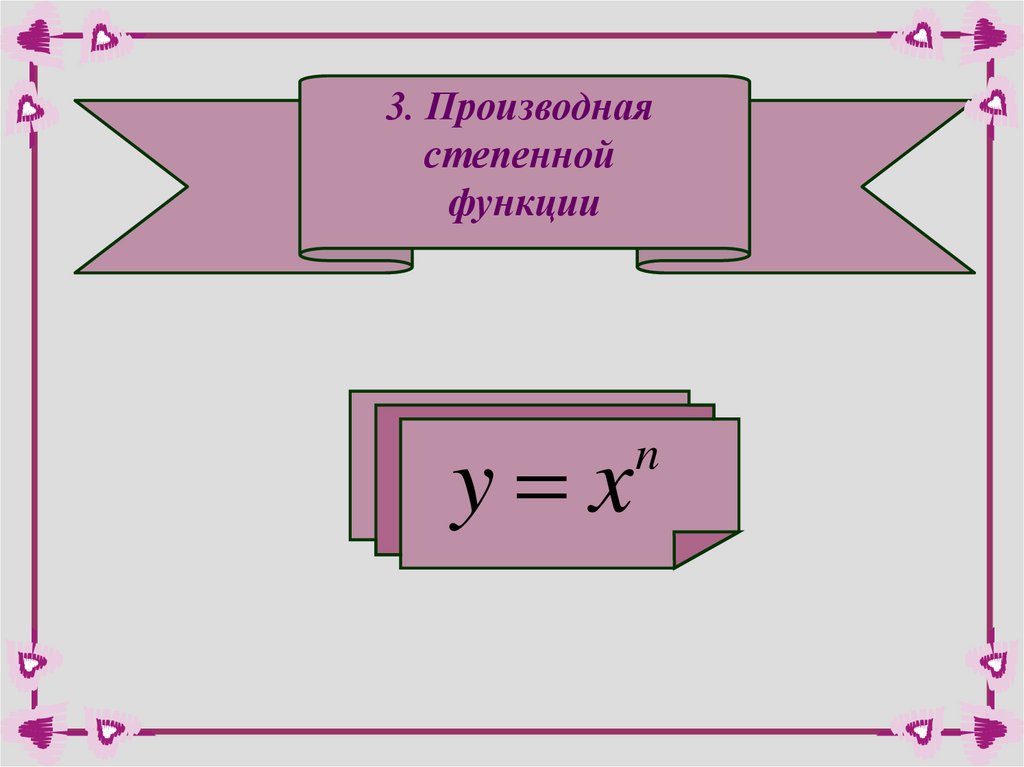
3. Производнаястепенной
функции
y x
n
21.
Логарифмируемоснованию e:
обе
части
равенства
ln y ln x n ln x
n
Дифференцируем обе части равенства по х:
(ln y ) (n ln x)
1
1
y n
y
x
по
22.
Отсюда выражаем искомую производную:1
y y n
x
Т.к.
y x
n
то окончательно получаем:
1
n 1
y n x n x
x
n
23.
( x ) n xn
n 1
Для сложной функции:
(u ) n u u
n
n 1
24.
4. Производнаястепеннопоказательной
функции
y f ( x)
( x)
25.
Логарифмируемоснованию e:
обе
части
ln y ln f ( x)
( x)
равенства
по
( x) ln f ( x)
Дифференцируем обе части равенства по х,
учитывая, что в правой части стоит
произведение:
(ln y ) ( x ) ln f ( x )
26.
1y ( x) ln f ( x) ln f ( x) ( x)
y
1
1
y ( x) ln f ( x)
f ( x) ( x)
y
f ( x)
1
y y ( x) ln f ( x)
f ( x) ( x)
f ( x)
27.
y f ( x)( x)
Т.к.
то окончательно получаем:
y f ( x)
( x)
f ( x)
( x)
1
( x) ln f ( x)
f ( x) ( x)
f ( x)
( x) ln f ( x) f ( x)
( x ) 1
f ( x) ( x)
28.
Чтобы продифференцироватьстепенно-показательную функцию,
ее сначала нужно
продифференцировать как
показательную функцию, а затем
как степенную и полученные
результаты сложить.
29.
ПРИМЕР.y x
x
x
n 1
x
x
y ( x ) x x x ln x x (1 ln x)
30.
ЗАМЕЧАНИЕПроизводная логарифмической функции
1
(ln y) y
y
называется
логарифмической
производной. Ее удобно использовать для
дифференцирования
функции,
выражение
которой
существенно
упрощается при логарифмирования.
31.
ПРИМЕР.( x 1)( x 2)
y
3 x
2
32.
Логарифмируемоснованию e:
обе
части
равенства
по
( x 1)( x 2)
ln y ln
3 x
2
Используем свойства логарифма:
1 ( x 1)( x 2 2)
ln
2
3 x
1
2
ln( x 1) ln( x 2) ln( 3 x)
2
33.
Дифференцируем обе части равенства по х:1
2
(ln y ) ln( x 1) ln( x 2) ln( 3 x)
2
1
1 1
2x
1
y
2
y
2 x 1 x 2 3 x
1 1
2x
1 ( x 1)( x 2 2)
y
2
2 x 1 x 2 3 x
3 x
34.
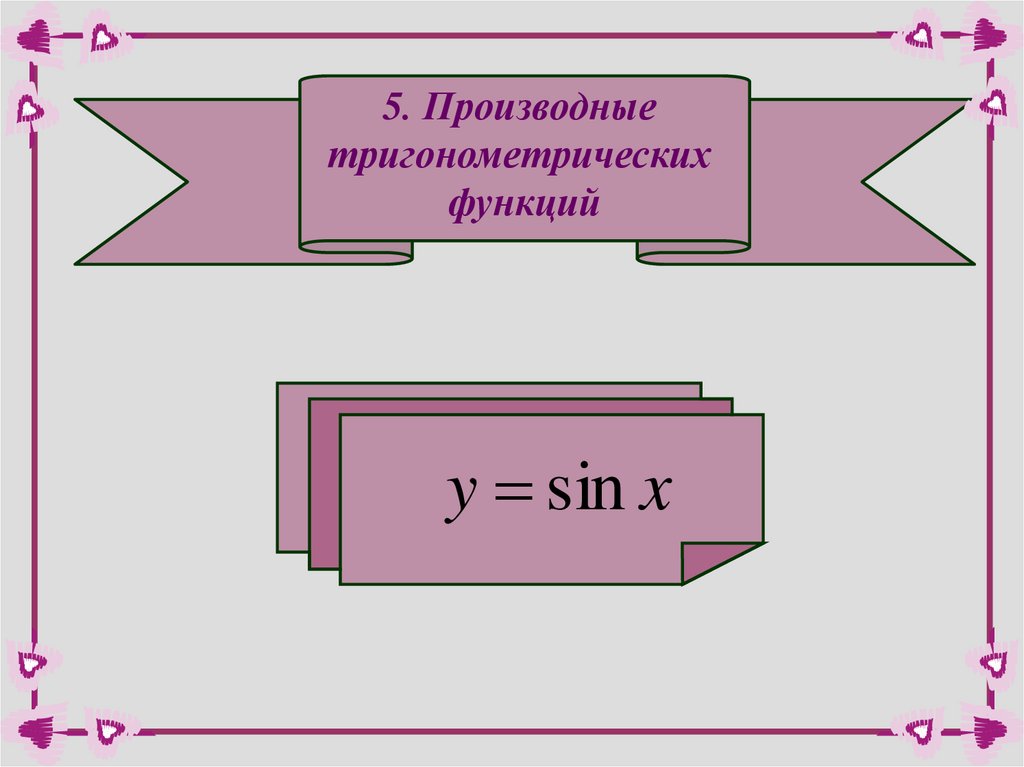
5. Производныетригонометрических
функций
y sin x
35.
Используем схему нахождения производной:Дадим аргументу х приращение Δх и найдем
значение функции y+Δy:
y y sin( x x)
Находим приращение функции
y sin( x x) sin x
Распишем разность синусов:
x
x
2 sin
cos x
2
2
36.
Составляем отношениеx
x
2 sin
cos x
y
2
2
x
x
Находим предел этого отношения:
x
x
2 sin
cos x
y
2
2
y lim
lim
x 0 x
x 0
x
37.
x2 sin
x
2
lim
lim cos x
x 0
x 0
x
2
cos x
Первый
предел
замечательному:
сводим
к
x
sin
2
lim
cos x cos x
x 0 x
2
1
первому
38.
(sin x) cos xДля сложной функции:
(sin u ) cos u u
39.
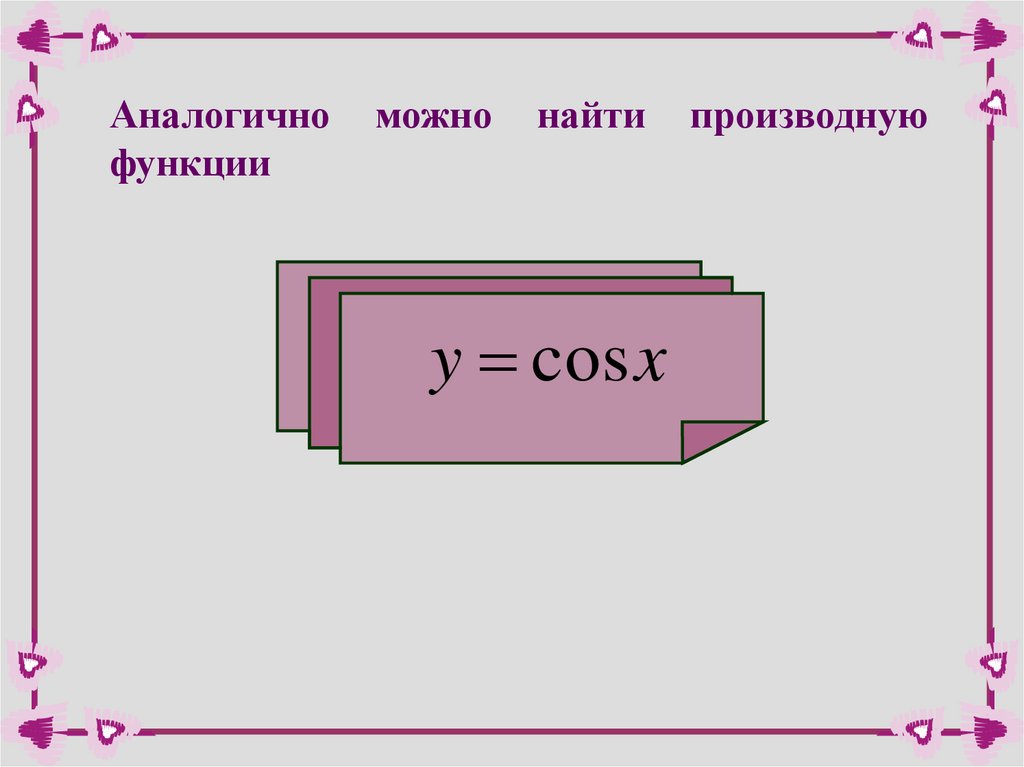
Аналогичнофункции
можно
найти
y cos x
производную
40.
(cos x) sin xДля сложной функции:
(cos u ) sin u u
41.
ПРИМЕР.sin 6 x
y
cos(x 2 1)
2
2
(sin 6 x) cos( x 1) sin 6 x (cos( x 1))
y
2
2
(cos( x 1))
6 cos 6 x cos( x 2 1) sin 6 x sin( x 2 1) 2 x
(cos( x 2 1)) 2
42.
Найдем производную функцииy tgx
43.
sin xy (tgx)
cos x
Находим производную дроби:
(sin x) cos x sin x (cos x)
2
cos x
1
cos 2 x sin 2 x
1
2
2
cos x
cos x
44.
1(tgx)
cos 2 x
Для сложной функции:
1
(tgu)
u
cos2 u
45.
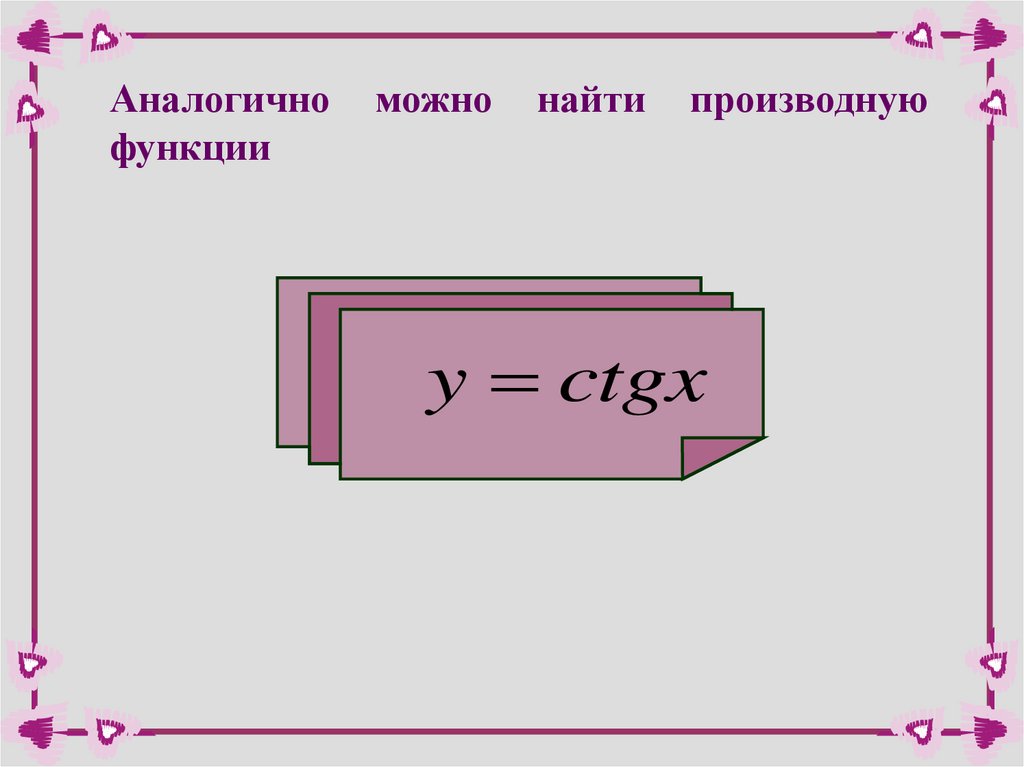
Аналогичнофункции
можно
найти
производную
y ctgx
46.
1(ctgx) 2
sin x
Для сложной функции:
1
(ctgu) 2 u
sin u
47.
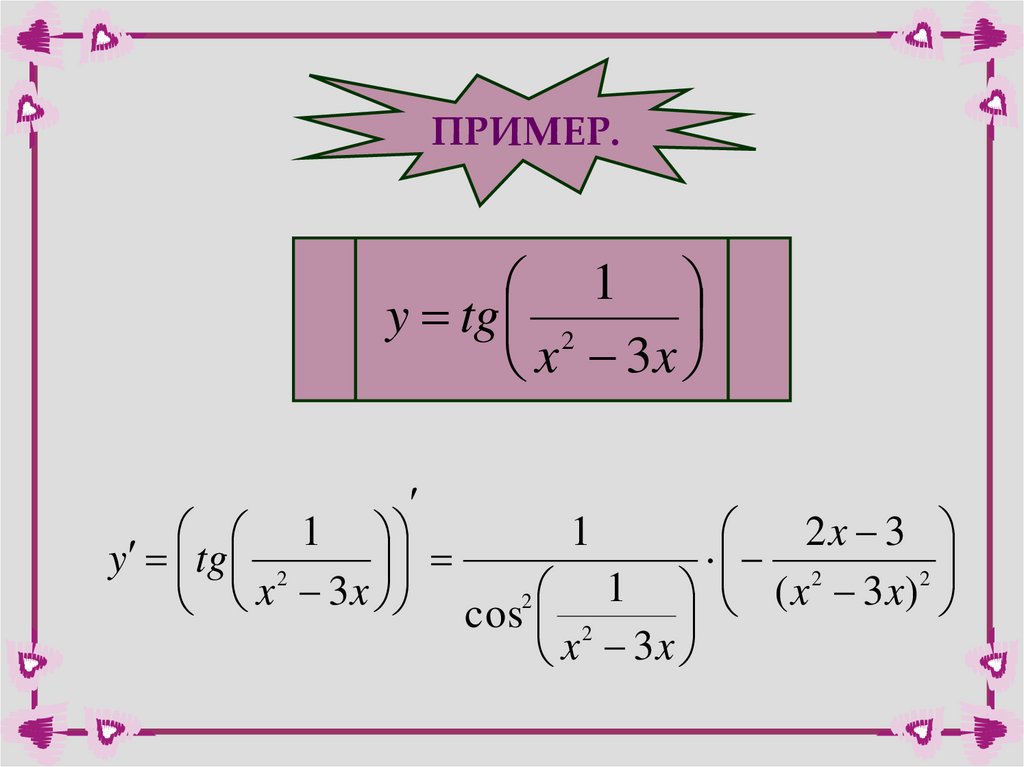
ПРИМЕР.1
y tg 2
x 3x
1
2x 3
1
y tg 2
2
2
x 3x cos2 1 ( x 3x)
2
x
3x
48.
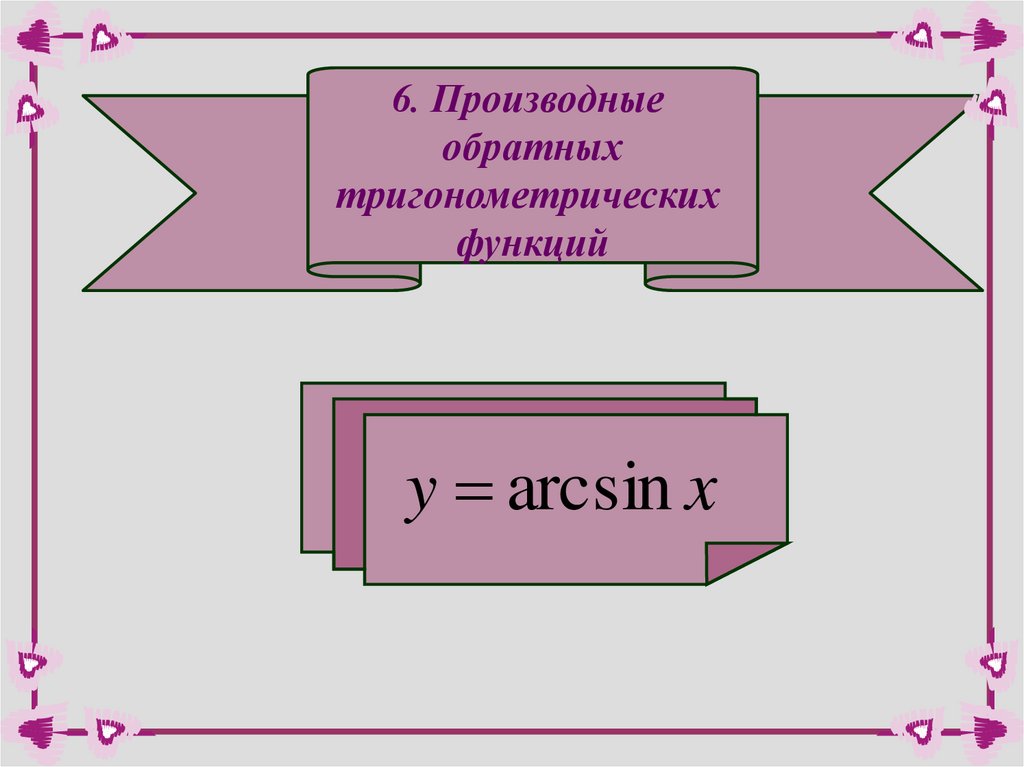
6. Производныеобратных
тригонометрических
функций
y arcsin x
49.
Обратной к ней функцией будет x sin yИспользуем правило дифференцирования
обратной функции:
1
1
1
xy
y x
y x
x y
cos y
Теперь нужно выразить у через х с помощью
основного тригонометрического соотношения:
1
1
1
(arcsin x)
2
2
cos y
1 sin y
1 x
x2
Эта производная не существует при
x 1
50.
(arcsin x)1
1 x2
Для сложной функции:
1
(arcsin u )
u
2
1 u
51.
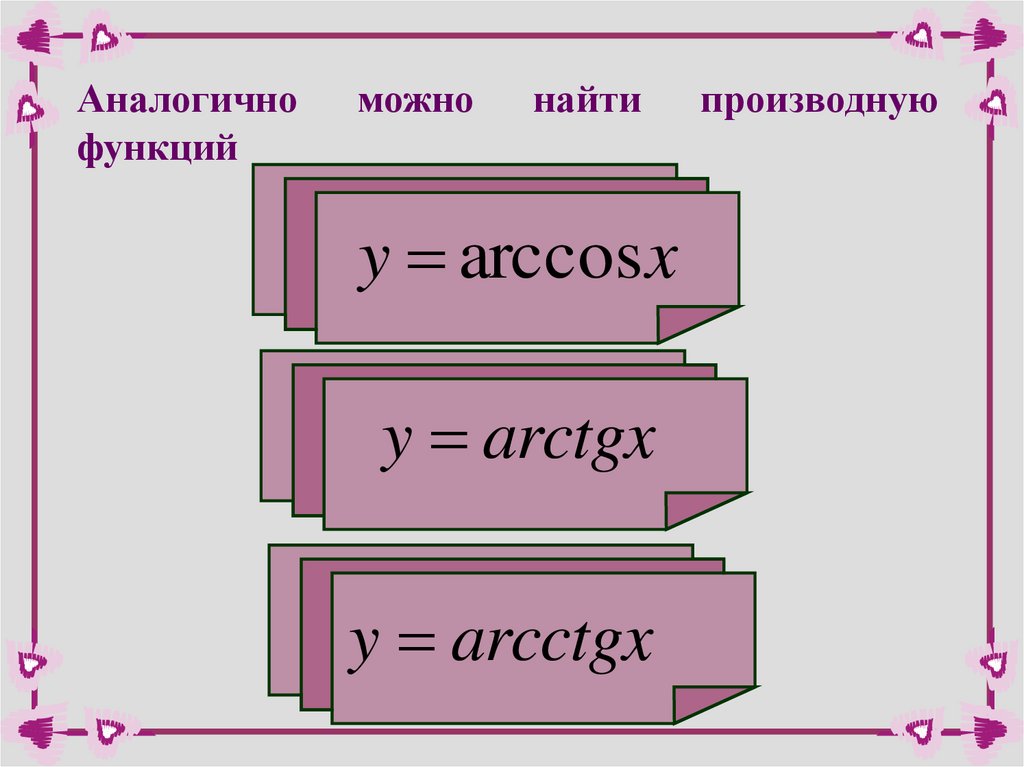
Аналогичнофункций
можно
найти
y arccos x
y arctgx
y arcctgx
производную
52.
(arccos x)1
1 x2
Для сложной функции:
1
(arccosu )
u
2
1 u
53.
1(arctgx)
2
1 x
Для сложной функции:
1
(arctgu)
u
2
1 u
54.
1(arcctgx)
1 x2
Для сложной функции:
(arcctgu)
1
u
2
1 u
55.
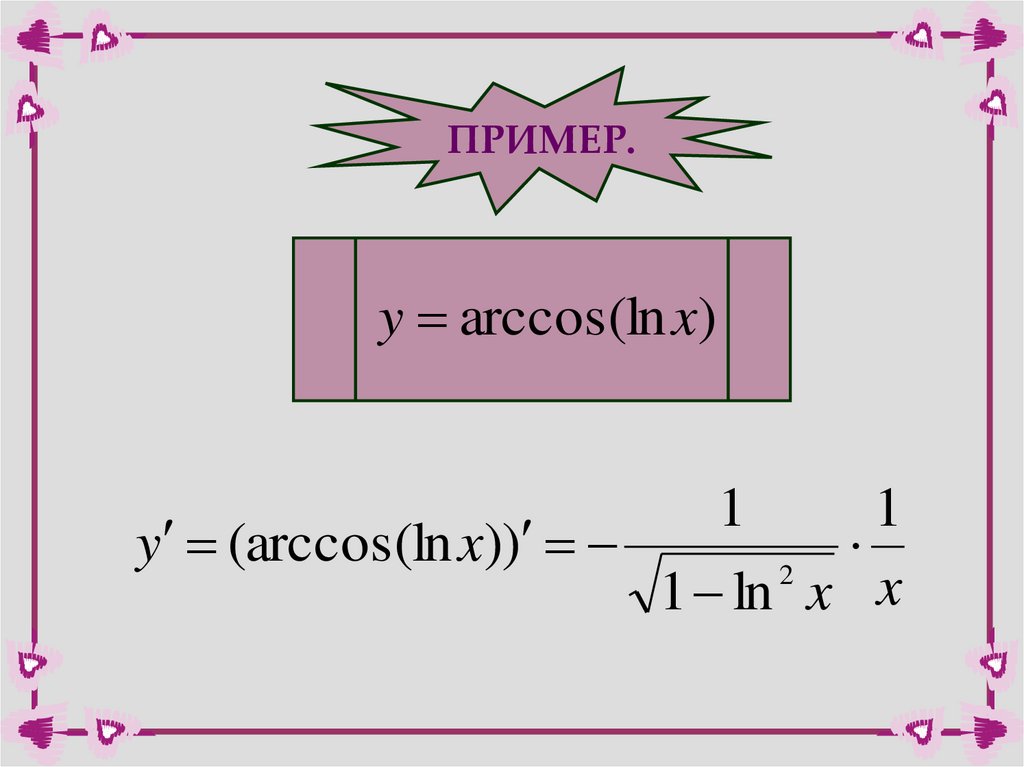
ПРИМЕР.y arccos(lnx)
1
1
y (arccos(ln x))
2
1 ln x x














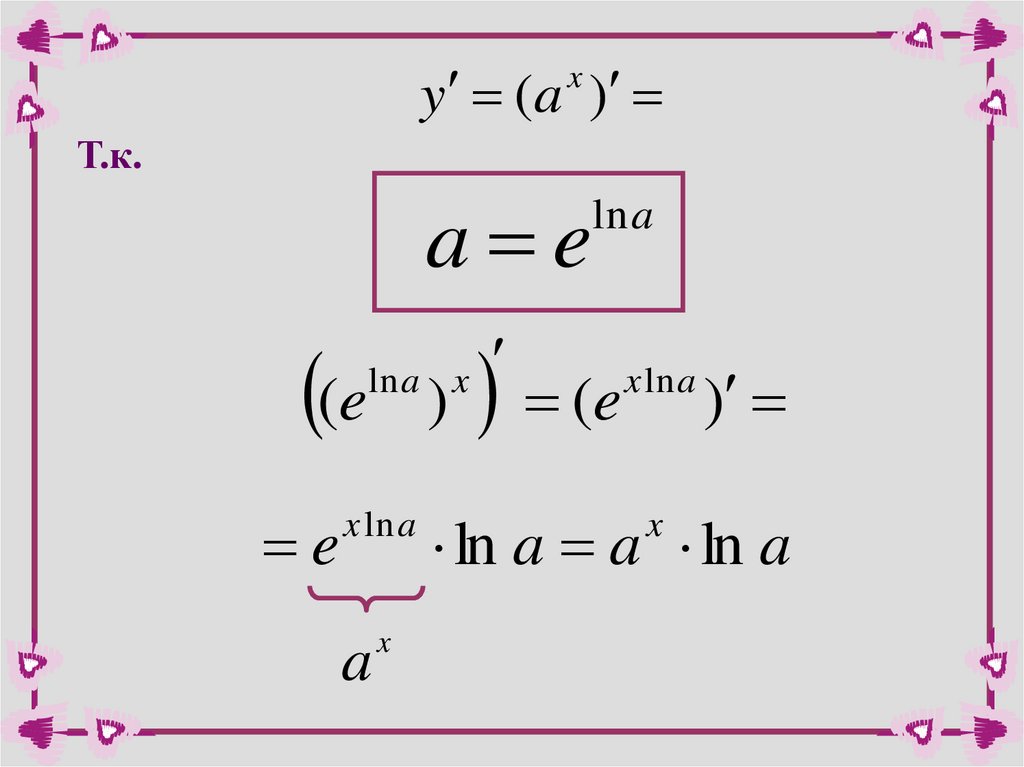







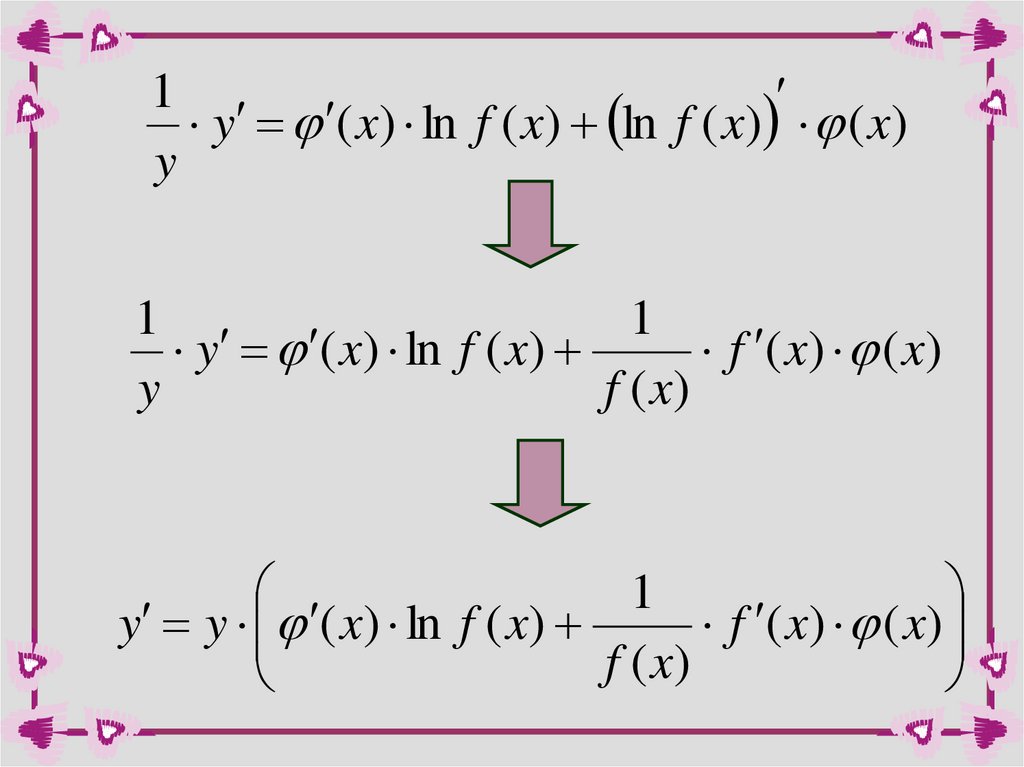












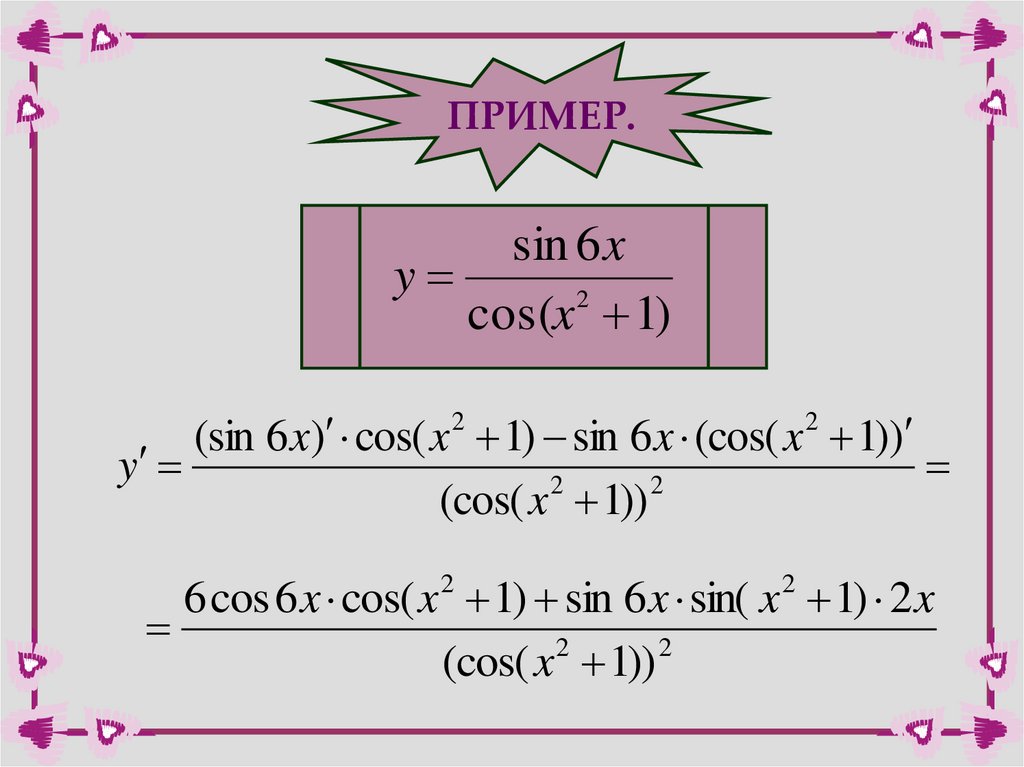
















 mathematics
mathematics








