Similar presentations:
Степенные ряды. Ряд Тейлора
1.
8. Степенные рядыРяд Тейлора
2.
Формула Тейлораf ( x0 )( x x0 ) f ( x0 )( x x0 ) 2
f ( x) f ( x0 )
...
1!
2!
f ( n ) ( x0 )( x x0 ) n
Rn ( x) Pn ( x) Rn ( x)
n!
f ( n 1) (c) ( x x0 ) n 1
Rn ( x)
c x0 ( x x0 ), 0 1
(n 1)!
f ( x) Pn ( x) Rn ( x)
Многочлен Тейлора
Остаточный член в
форме Лагранжа
3.
Ряд ТейлораЕсли функция y=f(x) имеет производные любых порядков
в окрестности точки х0, то из формулы Тейлора получаем
разложение в ряд Тейлора по степеням (х – х0).
f ( x0 )( x x0 ) f ( x0 )( x x0 ) 2
f ( n ) ( x0 )( x x0 ) n
f ( x0 )
...
...
1!
2!
n!
f ( n ) ( x0 )( x x0 ) n
Pn (x) n-ая частичная сумма
n!
n 0
Ряд Маклорена
x0 0
f (0) x f (0) x 2
f ( n ) (0) x n
f ( n ) (0) x n
f (0)
...
...
1!
2!
n!
n!
n 0
4.
Теорема. Для того чтобы ряд Тейлора сходился кфункции f(х) в некоторой окрестности точки х0,
необходимо и достаточно, чтобы в этой окрестности
(для всех x из интервала сходимости) lim Rn ( x ) 0
n
Доказательство.
lim Pn ( x) f ( x)
n
lim Rn ( x) lim ( f ( x) Pn ( x)) f ( x) lim Pn ( x) 0
n
n
n
lim Rn ( x) 0
n
Pn ( x) lim ( f ( x) Rn ( x)) f ( x) 0 f ( x)
lim S n ( x) lim
n
n
n
5.
Теорема (достаточное условие сходимости ряда Тейлора).Если модули всех производных функции f(x) ограничены в
окрестности точки x0 одним и тем же числом М>0 | f ( n ) ( x) | M ,
то для любого х из этой окрестности ряд Тейлора функции f(x)
сходится к функции f(x), т.е. имеет место разложение
.
f ( n ) ( x0 )
f ( x)
( x x0 ) n
n!
n 0
Доказательство. x ( x ) n M 0 : | f ( n ) ( x) | M
0
n 1
(
x
x
)
f ( n 1) (c)
n 1
0
lim
(
x
x
)
lim
M
lim | Rn ( x) |
0
n (n 1)!
n
n
(n 1)!
( x x0 ) n 1
n 2
x x0
(
x
x
)
(n 1)!
0
0 1
lim
lim
(n 1)!
n 0
n
1
n n 2
n ( n 2)! ( x x )
0
x ( ; )
( x x0 ) n 1
lim
0
n
(n 1)!
lim Rn ( x) 0
n
6.
Разложение в степенной ряд основныхэлементарных функций
1. f ( x) e
x0 0
x
f (0) e0 1
x
x
f ( x ) (e ) e
f
(n)
( x) e
f (0) e0 1
f ( n ) (0) e0 1
x
x :| x | R | f
(n)
( x) | e
2
n
x
x
x
ex 1
...
...
1! 2!
n!
R
x ( ; )
7.
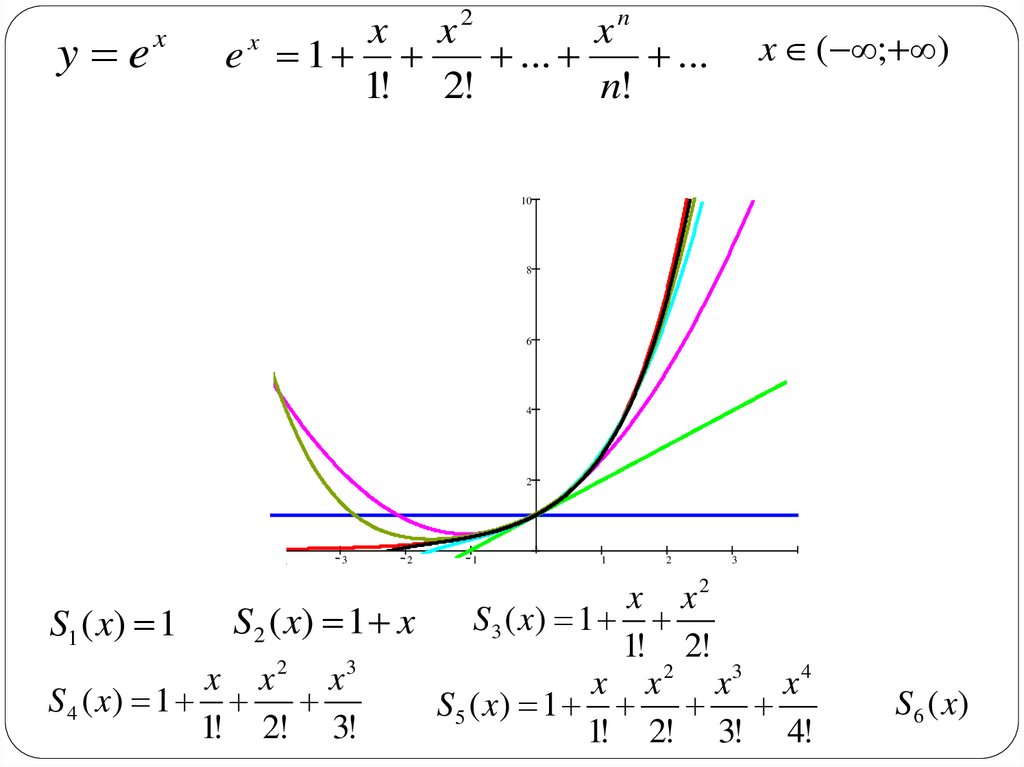
y ex
2
n
x
x
x
x
e 1
...
...
1! 2!
n!
x ( ; )
10
10 10
10
10
10
10
8
6
f ( x)fff(f(x(x(x)x)))
f ( x)
4
2
0
000
00 4
444
44
4
3
2
1
xxx0
xx
x
1
2
3
4444
44
4
x x2
S3 ( x) 1
S1 ( x) 1 S2 ( x) 1 x
1! 2!
2
3
x x
x
x x 2 x3 x 4
S 4 ( x) 1
S5 ( x) 1
1! 2! 3!
1! 2! 3! 4!
S 6 ( x)
8.
Разложение в степенной рядосновных элементарных функций
2. f ( x ) sin x
x0 0
f ( x) (sin x) cos x
f ( x) (cos x) sin x
f ( x) ( sin x) cos x
IV
f ( x) ( cos x) sin x
x : | f
(n)
f (0) sin 0 0
f (0) cos 0 1
f
(2k )
(0) 0
f ( 2 k 1) (0) ( 1) k
( x) | 1
x 3 x 5 x 7 x 9 x11
sin x x
...
3! 5! 7! 9! 11!
x ( ; )
9.
2 n 1x
x
x
x
x
( 1) x
sin x x
...
3! 5! 7! 9! 11!
(2n 1)!
n 0
3
5
7
9
11
n
у = sin x
1
111 1
f (xfx()ff)x((x)x) )
1 11 1
1
2 2
22
S1 ( x) x
xx
x
x ( ; )
3
x
S 2 ( x) x
3!
x3 x5 x7
S 4 ( x) x
3! 5! 7!
2
222
3
5
x
x
S3 ( x) x
3! 5!
x3 x5 x7 x9
S5 ( x) x
3! 5! 7! 9!
10.
Разложение в степенной рядосновных элементарных функций
3. f ( x ) cos x
x0 0
2 n 1
( 1) x
sin x
(2n 1)!
n 0
n
x ( ; )
Применяем свойства равномерно сходящихся рядов
x
x
x
( 1) x
(sin x) x ...
...
3! 5! 7!
(2n 1)!
3
5
7
n
2 n 1
2n
3x 2 5 x 4 7 x 6
(
2
n
1
)
x
cos x 1
... ( 1) n
...
3!
5!
7!
(2n 1)!
2n
x
( 1) n
(2n)!
n 0
x ( ; )
11.
Биномиальный ряд( 1) 2
( 1)...( n 1) n
(1 x) 1 x
x ...
x ...
1!
2!
n!
Интервал сходимости x ( 1; 1)
[ 1;1], 0,
x ( 1;1], 1 0,
( 1;1), 1
12.
Частные случаи биномиального ряда1
1 2 1 3
5 4
1 x 1 x x x
x ...
2
8
16
128
1
1 2 5 3 10 4
3
1 x 1 x x x
x ...
3
9
81
243
1
1 x x 2 x 3 x 4 ...
1 x
1
1
3 2 5 3 35 4
1 x x x
x ...
2
8
16
128
1 x
1
1
2 2 14 3 35 4
1 x x x
x ...
3
3
9
81
243
1 x
1
1 x x 2 x 3 x 4 ...
1 x
13.
11 x x 2 ... x n ...
1 x
S ( x)
S8 ( x) 10
S 7 ( x)
S5 ( x)
10
10
10
8
6
ff((xx))
S3 ( x)
4
S 6 ( x)
2
00
1.5
1
0.5
1.5
1.5
Область сходимости
0
0.5
1
xx
1.5
1.5
1.5
x ( 1; 1)
14.
11 x x 2 x 3 x 4 ...
1 x
x ( 1; 1)
x
1
x
0 1 t dt ln | 1 t | 0 ln | 1 x | ln 1 ln( 1 x)
x
(1 t t t t ... ( 1) t ...)dt
2
0
2
3
3
4
n
n
x
n 1
4
t
t
t
n t
t ... ( 1)
...
2 3 4
n 1
0
2
3
4
n 1
x
x
x
n x
x ... ( 1)
...
2
3 4
n 1
15.
у = ln(1+ x) – исходная функциях 2 х3 х 4
Разложение функции в ряд ln( 1 x) x ...
2
3
4
16.
n 1n 1
x2 x3
x
x
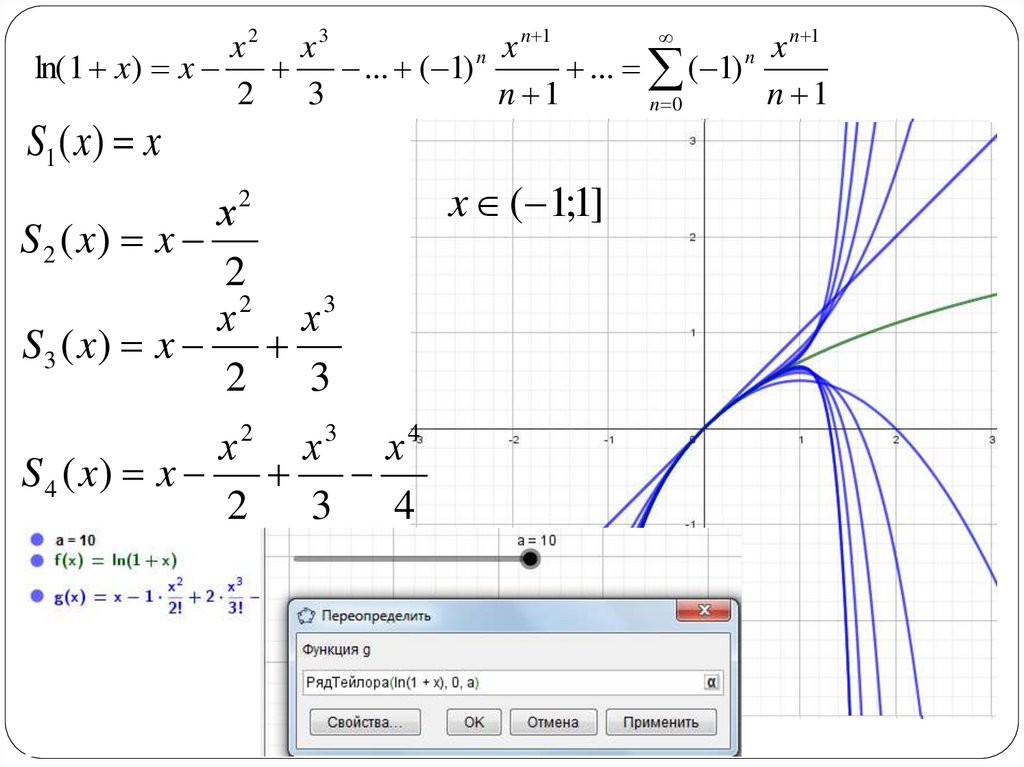
ln( 1 x) x
... ( 1) n
... ( 1) n
2
3
n 1
n 1
n 0
S1 ( x) x
х2
S 2 ( x) x
2
х 2 х3
S3 ( x) x
2 3
х 2 х3 х 4
S 4 ( x) x
2 3 4
x ( 1;1]
17.
32 n 1
5
x
x
n x
arctgx x
... ( 1)
...
3
5
2n 1
x
dx
0 1 x 2 arctgx
x [ 1;1]
1
1 x x 2 x 3 x 4 ...
1 x
1
2
4
6
8
1
x
x
x
x
...
2
1 x
x
x
dx
2
4
6
n 2n
0 1 x 2 (1 x x x ... ( 1) x ...)dx
0
2 n 1
( 1)
( 1)
x 1 ( 1)
2n 1
n 0
n 0 2n 1
n
n
x 1 ( 1)
n 0 2n 1
n
18.
xdx
1 x arcsin x
2
0
1
1
3 2 5 3 35 4
1 x x x
x ...
2
8
16
128
1 x
1
1
3 2 5 3 35 4
1 x x x
x ...
2
8
16
128
1 x
1
1 2 3 4 5 6
1 3 5...( 2n 1) 2 n
1 x x x ... 1
x
2
2
8
16
1 x
n 1 2 4 6...( 2n )
(2n 1)!! 2 n
(2n 1)!! 2 n
x
1
x 1 n
2 n!
n 1
n 1 ( 2n)!!
2 n 1
(2n 1)!! x
arcsin x x n
2 n! 2n 1
n 1
x [ 1;1]
19.
Некоторые приложения степенныхрядов
Приближенные вычисления
значений функций. f ( x0 ) S n ( x0 )
Приближенные вычисления
определенных интегралов.
Приближенные решения
дифференциальных уравнений.
20.
1. Вычислить число е с точностью до ε=0,0012
n
x
x
x
ex 1
...
...
1! 2!
n!
2
n
1
1
1
1 1
1
1
e 1 ... ... 1 1 ... ...
1! 2!
n!
2 6
n!
1 1
1
e 1 1 ...
2 6
n!
1
1
1
1
1
1
| Rn (1) |
...
...
(n 1)! (n 2)!
(n 1)! n 2 (n 2)( n 3)
1
1
1
1
1
1
1
...
2
(n 1)! n 1 (n 1)
n! n
(n 1)! 1 1
n 1
1
1
1
1
| Rn (1) |
0,001
n! n
6! 6 4320 1000
21.
1. Вычислить число е с точностью до ε=0,0012
n
x
x
x
ex 1
...
...
1! 2!
n!
1 1 1 1 1
e 1 1
n 6
2! 3! 4! 5! 6!
e 1 1 0,5 0,1667 0,417 0,0083 0,0014 2,7181
С точностью до ε=0,001 е=2,718
1
0,0002 0,001
7!
22.
2. Вычислить с точностью до ε=0,0001 значение интегралаx 3 x 5 x 7 x 9 x11
sin x x
...
3! 5! 7! 9! 11!
0,5
sin x
0 x dx
2
4
3
5
x
x
x
x
0,5
sin x
1 ... dx x
...
dx
0
0 x
3! 5!
3 3! 5 5!
0
3
5
0,5 0,5
0,125 0,03125
0,5
... 0,5
...
18 600
18
600
0,5
0,5
0,55
0,00005 0,0001
600
0,5
0,125
sin x
0 x dx 0,5 18 0,5 0,00694 0,49306
0,5
sin x
0 x dx 0,4931 с точностью до ε=0,0001












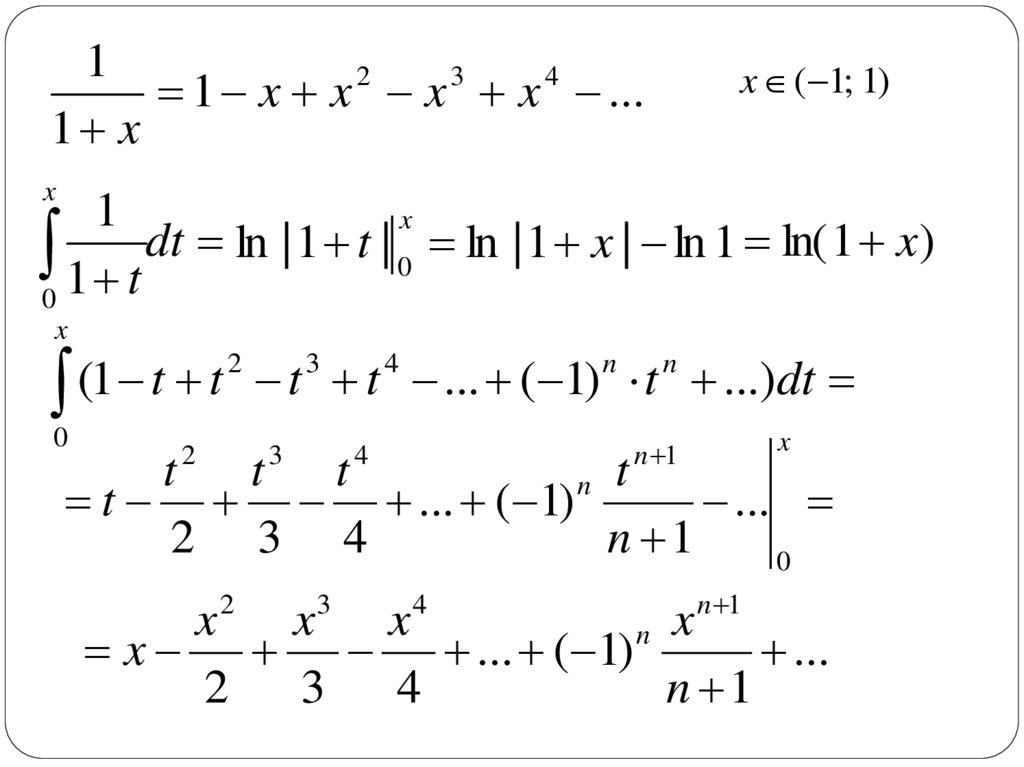

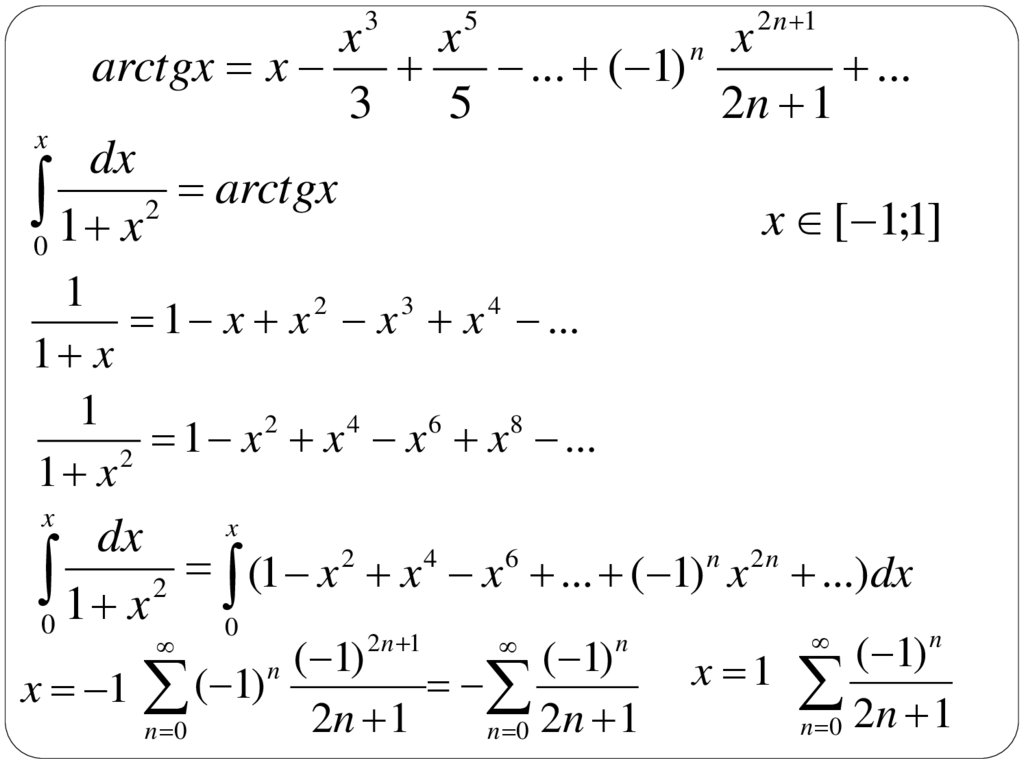





 mathematics
mathematics








