Similar presentations:
Вывод и решение дифференциального уравнения вертикальных колебаний фундамента
1.
Вывод и решениедифференциального уравнения
вертикальных колебаний
фундамента
2.
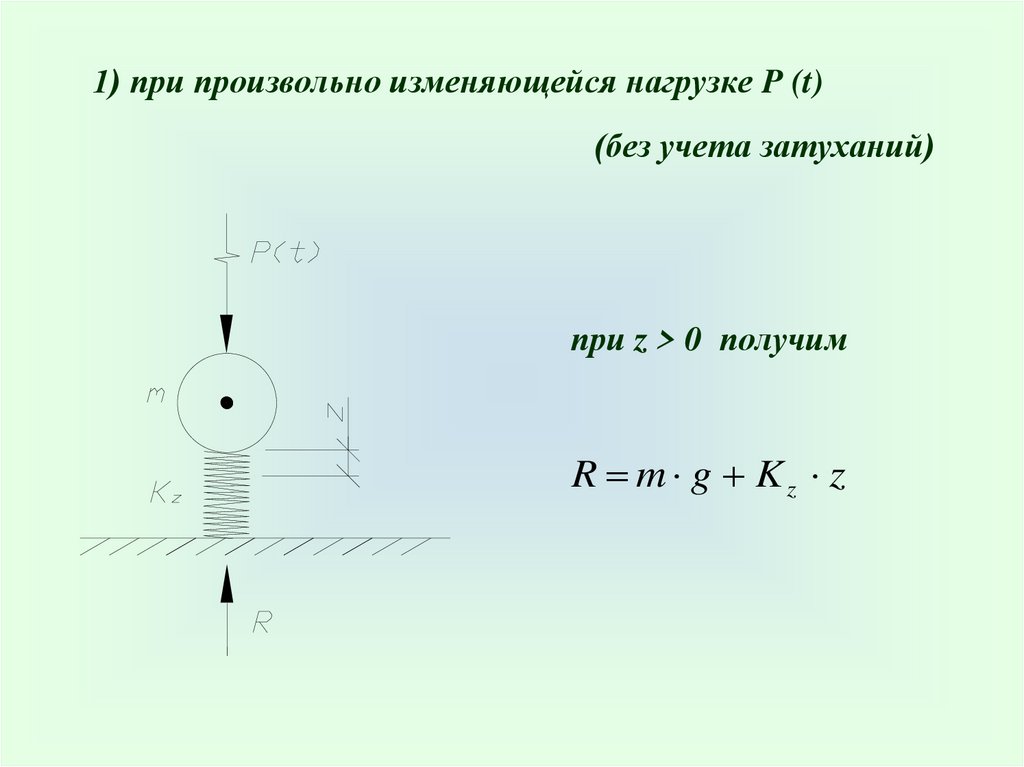
1) при произвольно изменяющейся нагрузке P (t)(без учета затуханий)
при z > 0 получим
R m g Kz z
3.
Для составления уравнения движения используетсяпринцип Даламбера:
«Уравнение движения может быть получено как уравнение движения в статике, если к внешним силам, действующих на систему, добавить силу инерции с обратным знаком по отношению направления движения».
4.
Q P(t ) m z // R,m z // Q P(t ) R 0,
т.к R m g K z z
m z Q P(t ) m g K z z 0,
//
m z // K z z P(t ),
5.
KzP(t)
z
z
,
m
m
//
2z
2 Kz
z
m
P(t)
z z
.
m
//
2
z
6.
2) при нагрузке P (t) = 0(свободные колебания)
z z 0
//
2
z
Решение данного уравнения:
z A sin z t B cos z t ,
где А и В – произвольные коэффициенты (получены из
начальных условий).
7.
при t = 0, z = 00 0 В 1
В 0
при t = 0, z / = v0ф
z / A z cos z t В z sin z t
A
z/
z
v0ф
z
az ,
8.
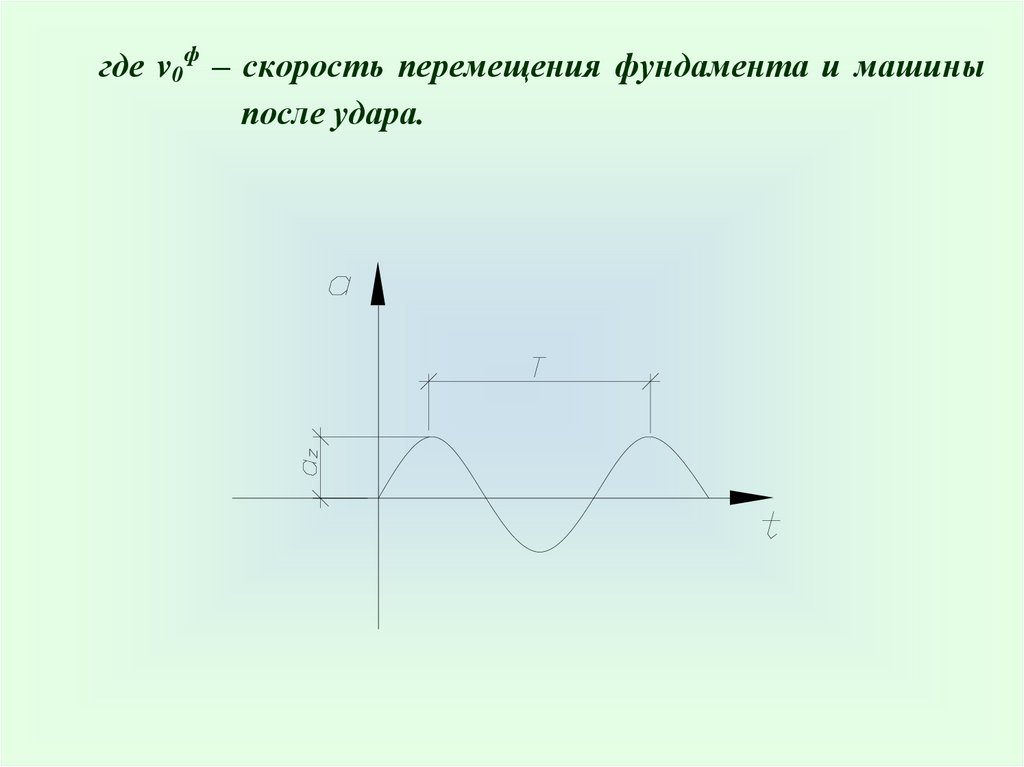
где v0ф – скорость перемещения фундамента и машиныпосле удара.
9.
1 m0 v0v
ф
0
m0 m
1 m0 v0
az
,
m0 m z
так как m0 m,
1 m0 v0
a
,
z
m z
(используется при расчете фундамента под молот)
10.
где m0 – масса ударной части;m – масса фундамента и машины;
v0 – скорость ударной части в момент соударения;
ε
– коэффициент восстановления удара;
λz – частота свободных (собственных) колебаний.
11.
3) при нагрузке P (t) = Pz · sin(ω · t) – гармоническиеколебания
здесь ω – частота динамического воздействия
(вынужденных колебаний);
t
– время (переменная).
Pz sin t
z z
m
//
2
z
Решение данного уравнения:
z аz sin t ,
z / аz cos t ,
z // аz sin t 2 .
12.
а z sin t а z sin t2
2
z
Pz sin t
m
Pz
аz ,
m
2
z
2
Pz
Pz
1
аz
2
2
2
2
m z
m z
1 2
z
,
13.
11 2
z
2
Pz
аz
аст ,
Kz
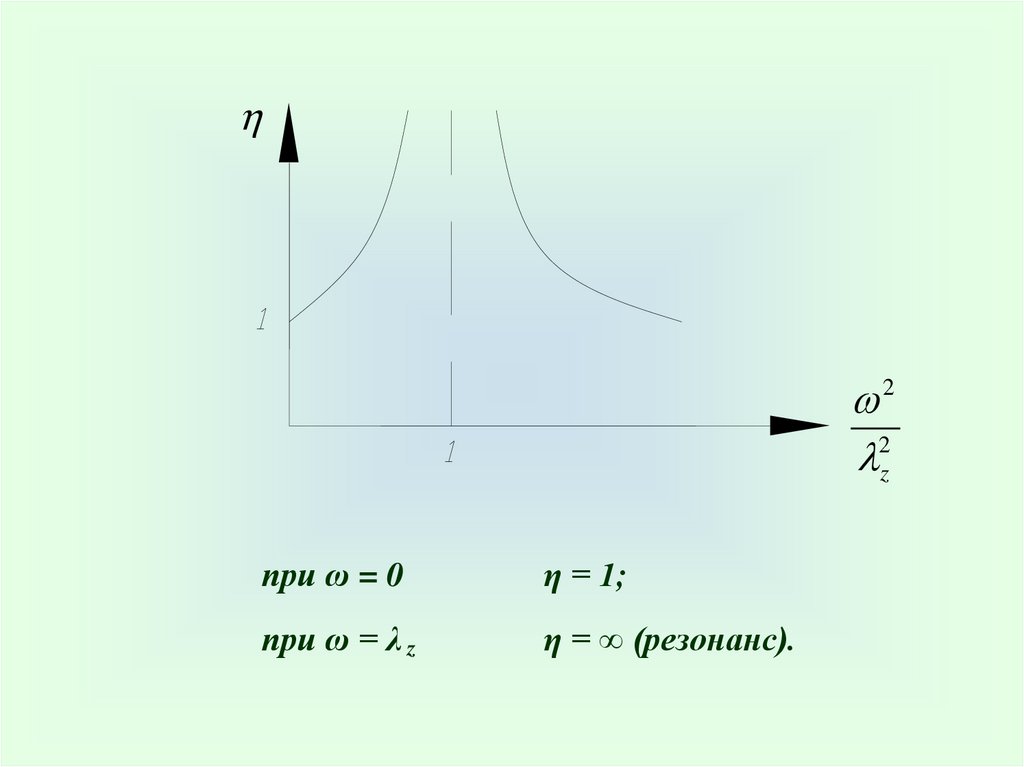
где η – коэффициент динамичности системы.
14.
22z
при ω = 0
η = 1;
при ω = λ z
η = ∞ (резонанс).
15.
С учетом затуханий:az
Pz
1
аст ,
2
Kz 2
1 2 Ф 2
z
2
Ф
,
z
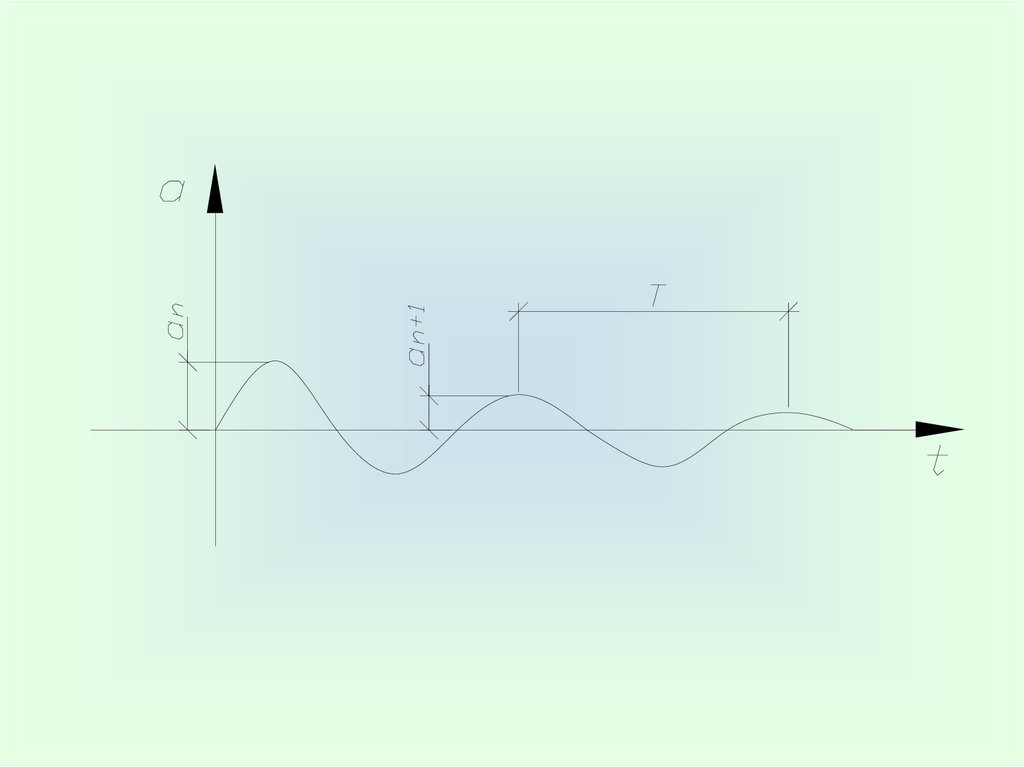
an
,
ln
an 1
где Ф
δ
– модуль затухания;
– логарифмический декремент затухания.
16.
17.
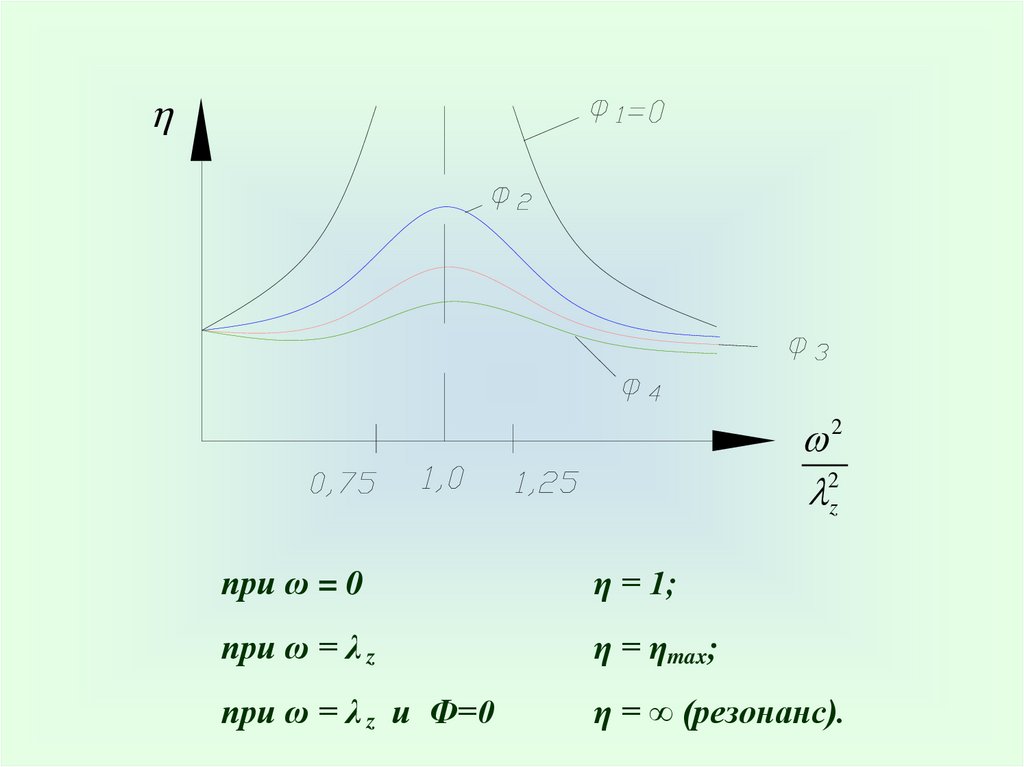
22z
при ω = 0
η = 1;
при ω = λ z
η = ηmax;
при ω = λ z и Ф=0
η = ∞ (резонанс).
18.
Упругиехарактеристики грунтов
и методы их определения
19.
Упругие характеристик грунтов:Е – модуль упругости;
G – модуль сдвига (Юнга);
υ – коэффициент Пуассона.
20.
Методы определения характеристик:1) по таблицам;
2) динамические методы;
3) статические методы.
экспериментальные
21.
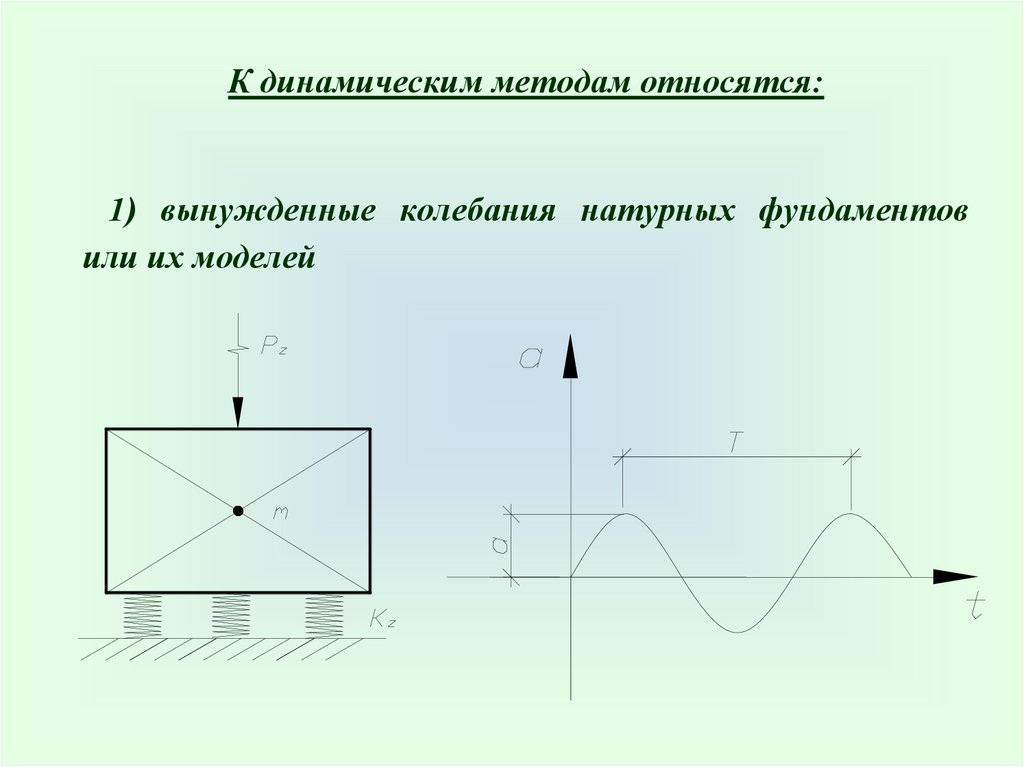
К динамическим методам относятся:1) вынужденные колебания натурных фундаментов
или их моделей
22.
Pza z m 2 2 ;
z
2 K z ;
z m
Kz
Pz
2 m;
az
Kz
Cz
A
23.
2 a b PC z C0 1
;
A P0
С0 17
E
1
2
1 C .
E
2
0
17
24.
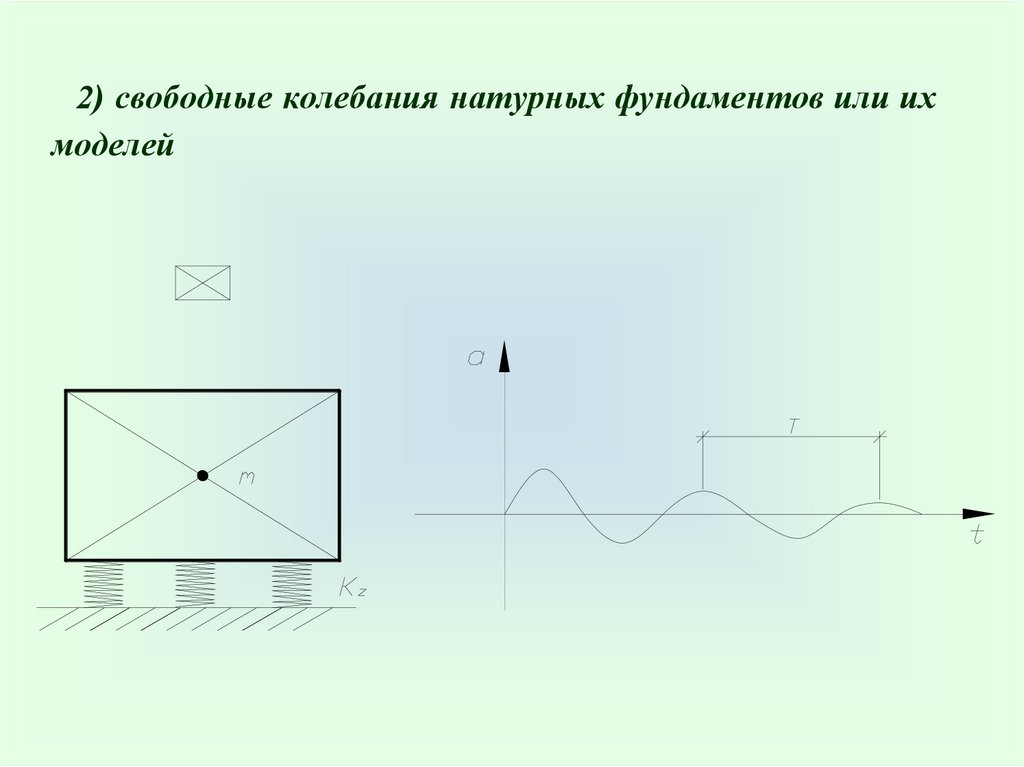
2) свободные колебания натурных фундаментов или ихмоделей
25.
2z
,
T
где λz – свободная частота колебаний фундамента;
Т – период колебаний.
26.
Kz;
m
2
z
K z 2z m;
Cz
Kz
A
27.
2 a b PC z C0 1
;
A P0
С0 17
E
1
2
1 C .
E
2
0
17
28.
Описанные выше методы используются, если на площадке имеются построенные фундаменты и возможность возбуждения колебаний.29.
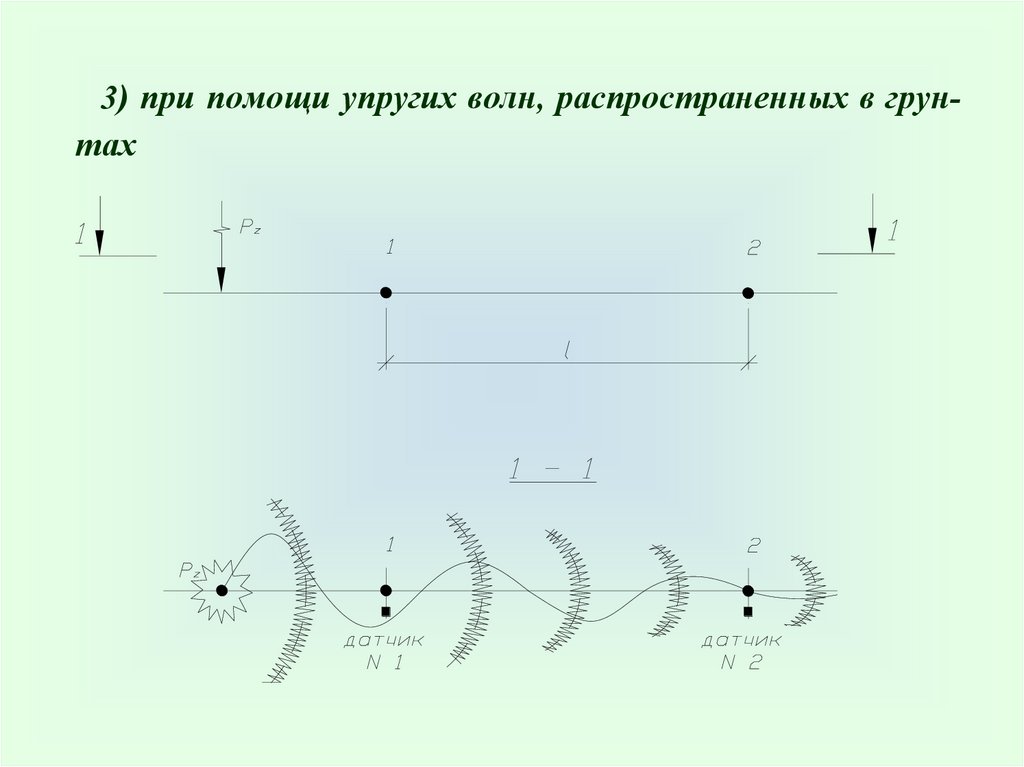
3) при помощи упругих волн, распространенных в грунтах30.
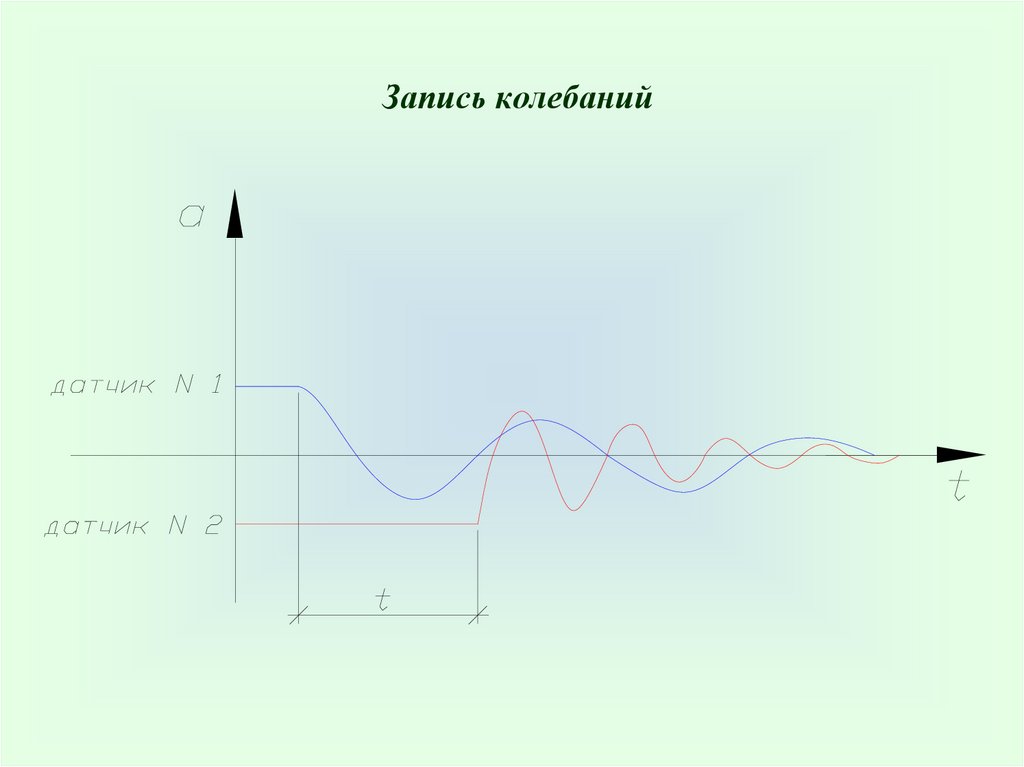
Запись колебаний31.
При ударе (взрыве) в грунте возникают:– продольные волны со скорость С1
(волны уплотнения, Р-волны);
– поперечные волны со скоростью С2
(волны сдвига, S-волны);
– плоские волны со скоростью, практически совпадающей со скоростью поперечных волн
(волны Релея).
32.
C11
E
;
1 1 2
G
C2
;
E 2 G 1 ;
C1 C2
g
;
2 1
.
1 2
33.
lC1 ,
tx
l
C2 .
ty
Например, в супесях:
С1 = 250 ÷ 300 м/сек;
С2 = 120 ÷ 150 м/сек;
Е = 76 ÷ 102 МПа;
G = 29 ÷ 40 МПа;
υ = 0,32 ÷ 0,34.
34.
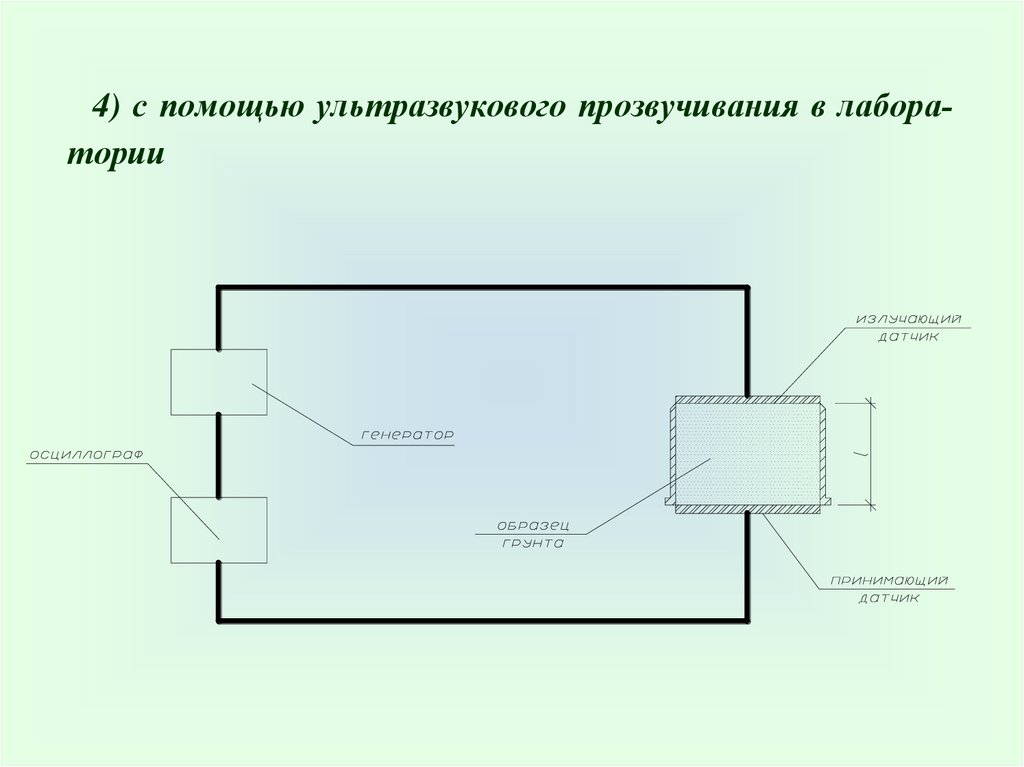
4) с помощью ультразвукового прозвучивания в лаборатории35.
lC ;
t
C G E,
36.
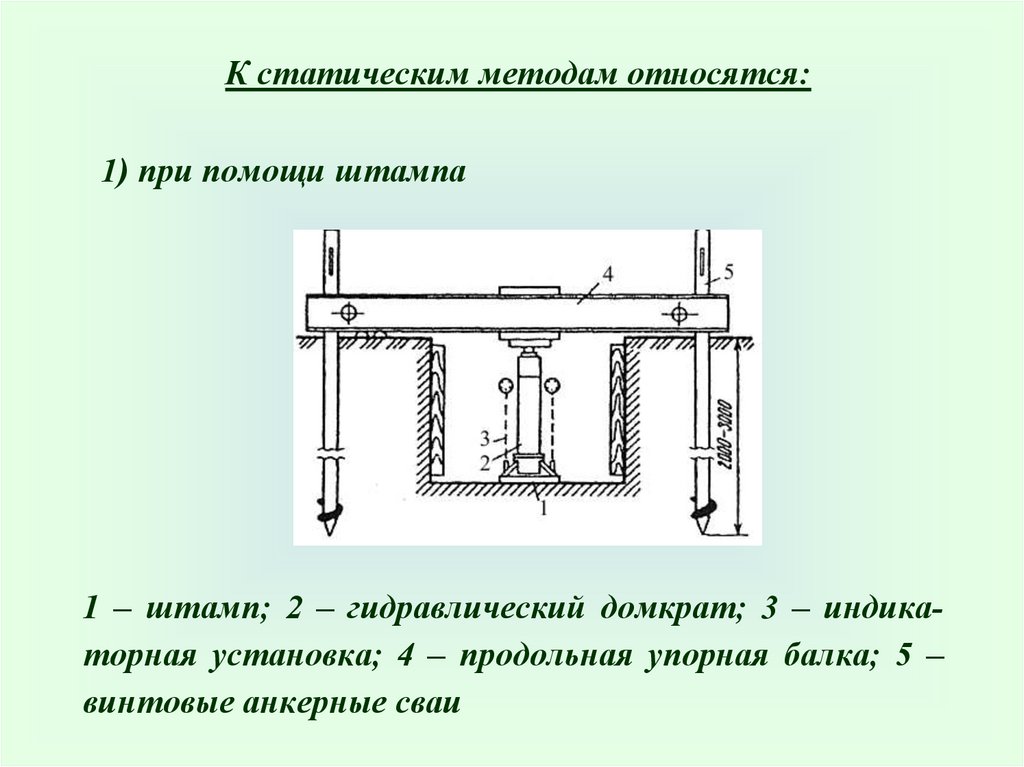
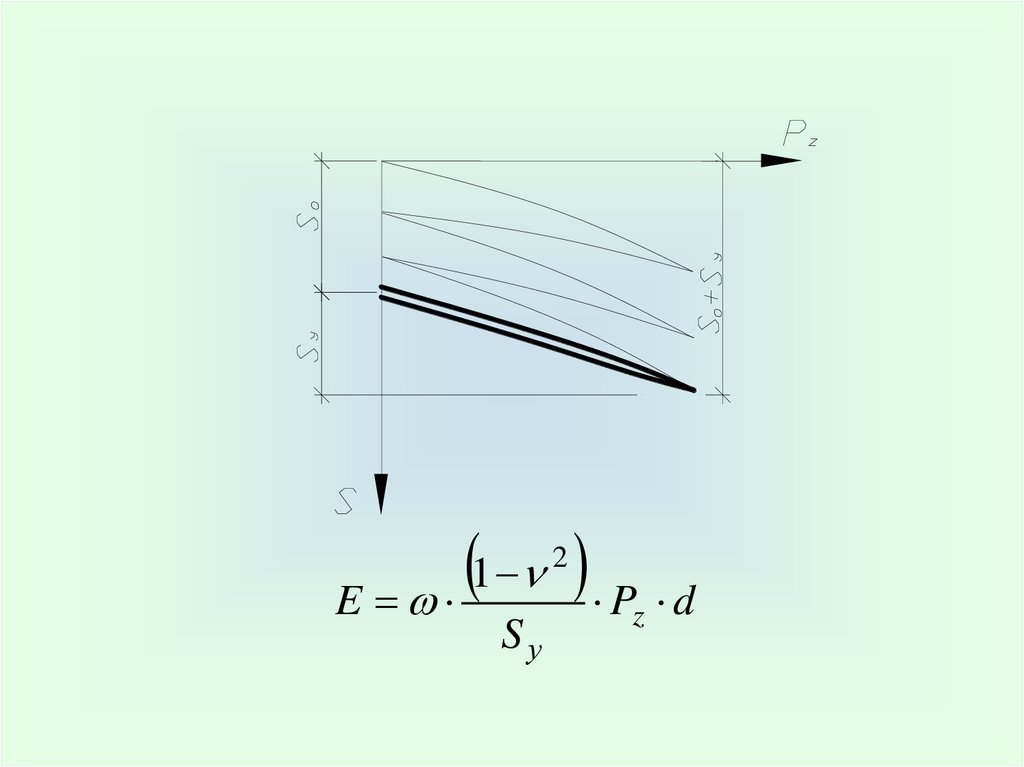
К статическим методам относятся:1) при помощи штампа
1 – штамп; 2 – гидравлический домкрат; 3 – индикаторная установка; 4 – продольная упорная балка; 5 –
винтовые анкерные сваи
37.
1E
P d
2
Sу
z
38.
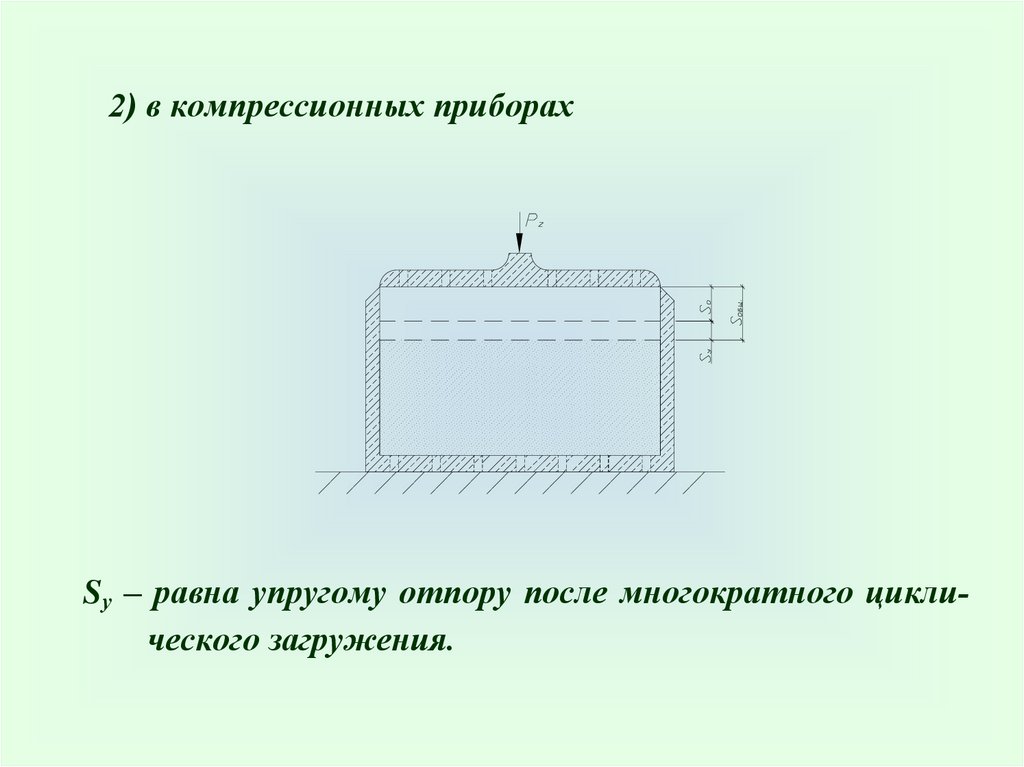
2) в компрессионных приборахSу – равна упругому отпору после многократного циклического загружения.
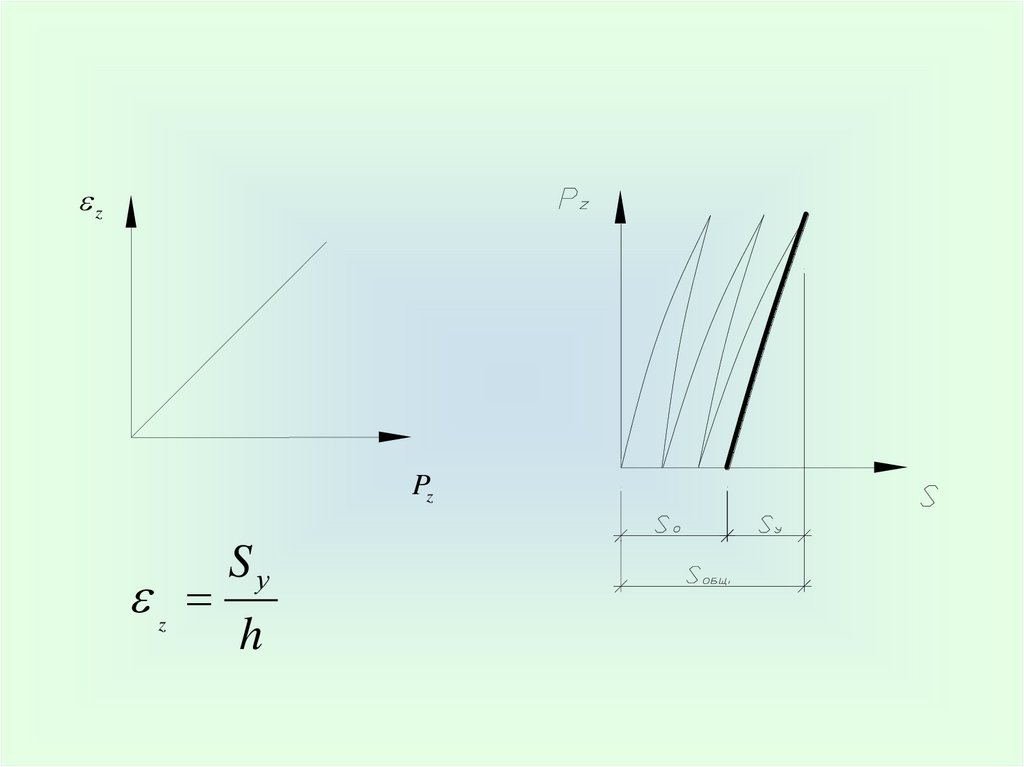
39.
zPz
z
Sу
h
40.
Закон Гука:x y
z
E
E
z
Pz 2 2
E 1
,
z 1
с учетом
x y Pz
1
Pz .
41.
№п/п
Наименование методов
Ei
Е с,к
1.
По частоте свободных колебаний
1
2.
По скорости распространения упругих
волн
0,95
3.
По результатам испытаний штампом
0,90
4.
По результатам компрессионных
испытаний
0,86
5.
Табличный
0,5 ÷ 1,1


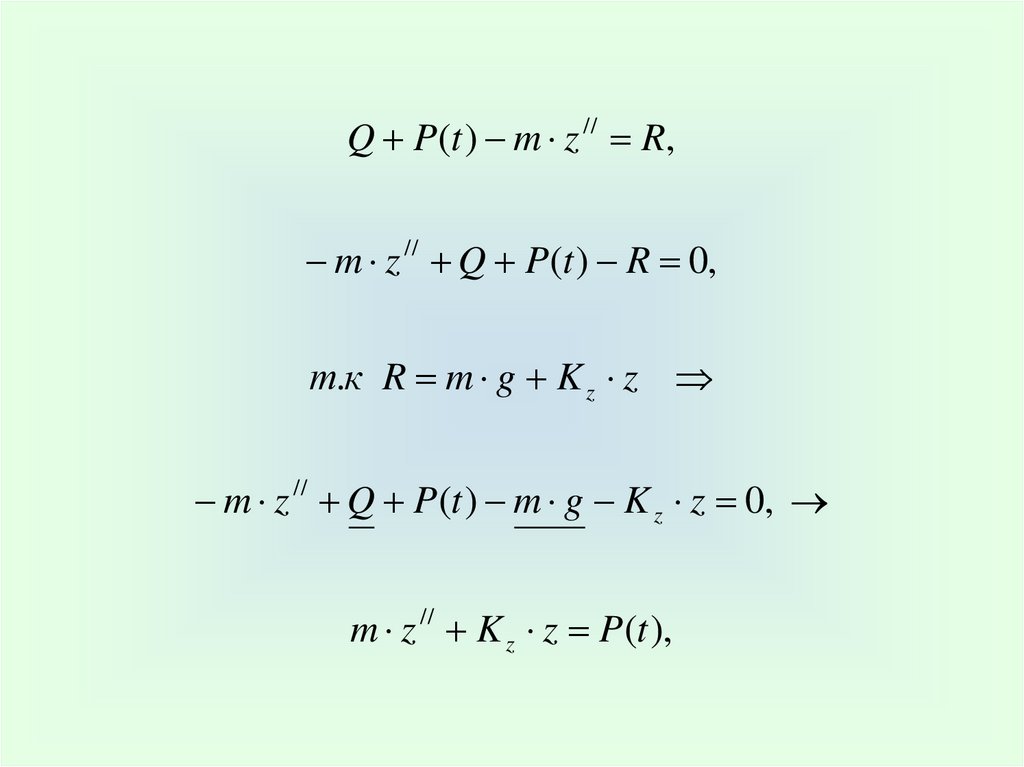
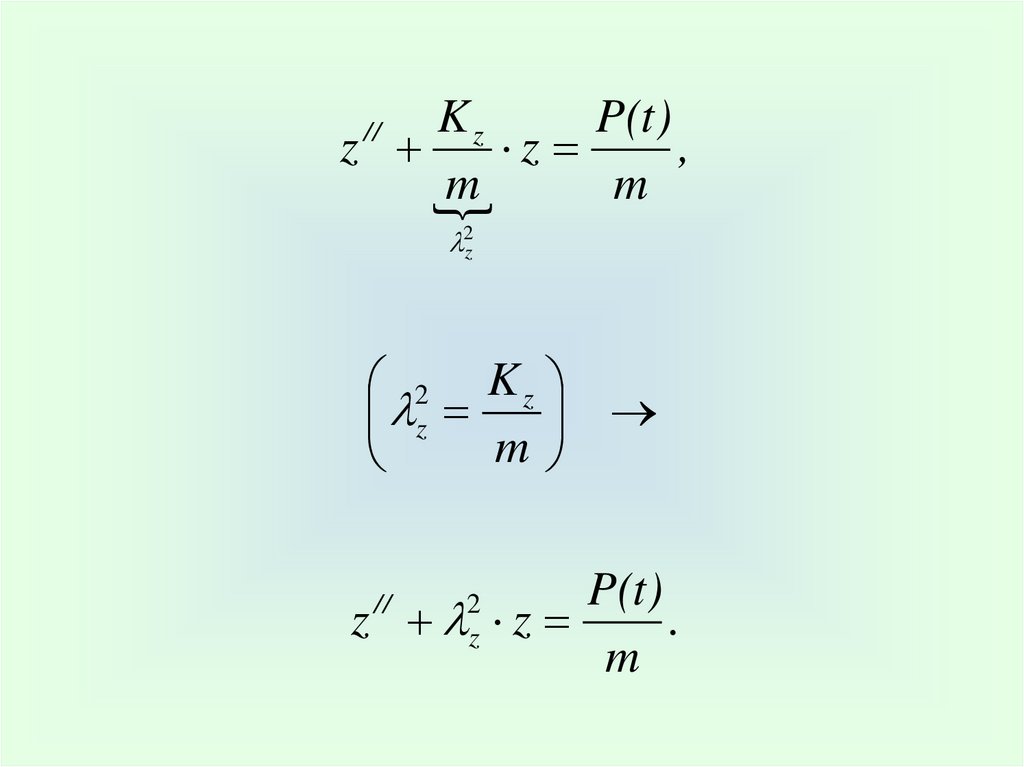

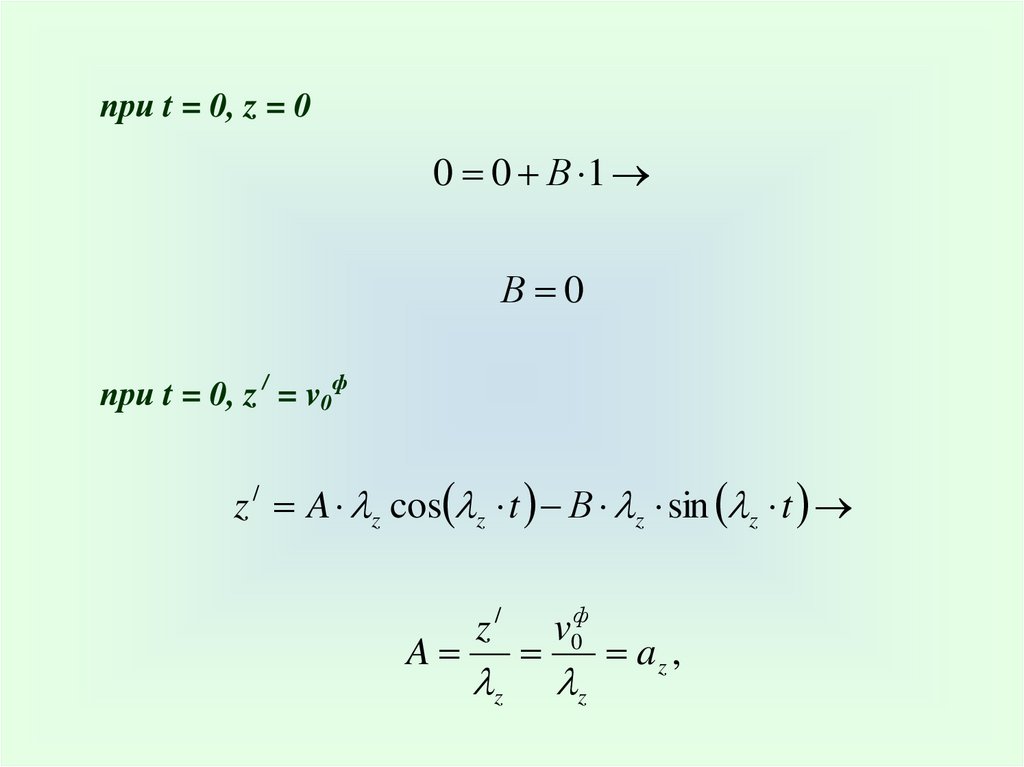



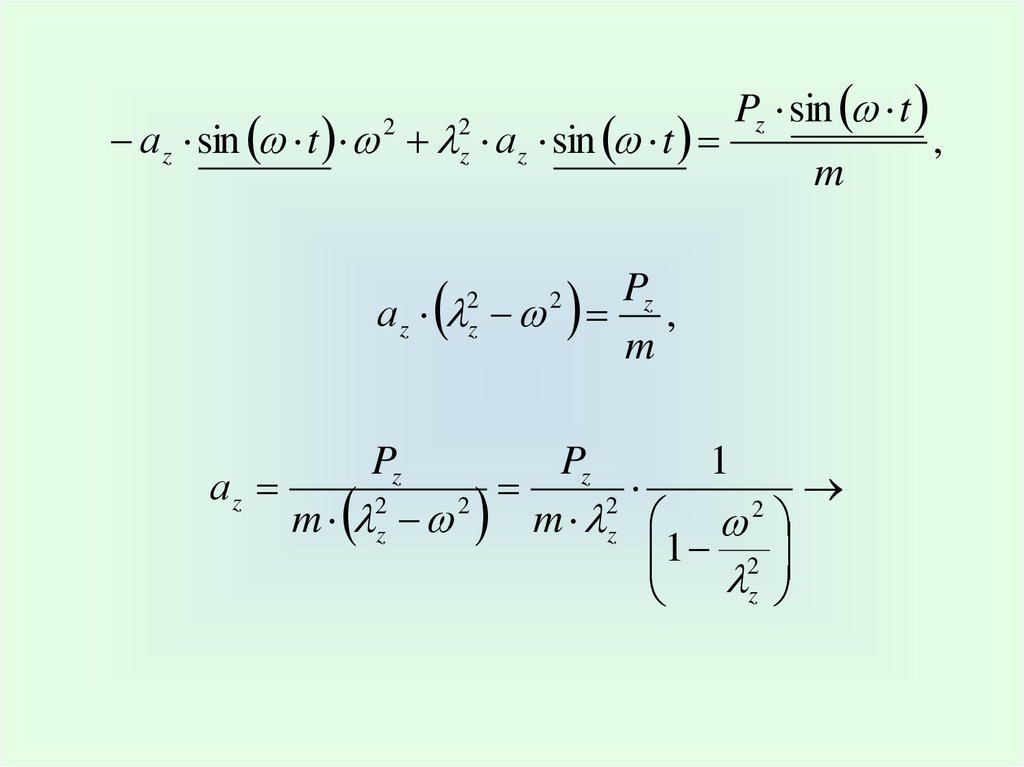






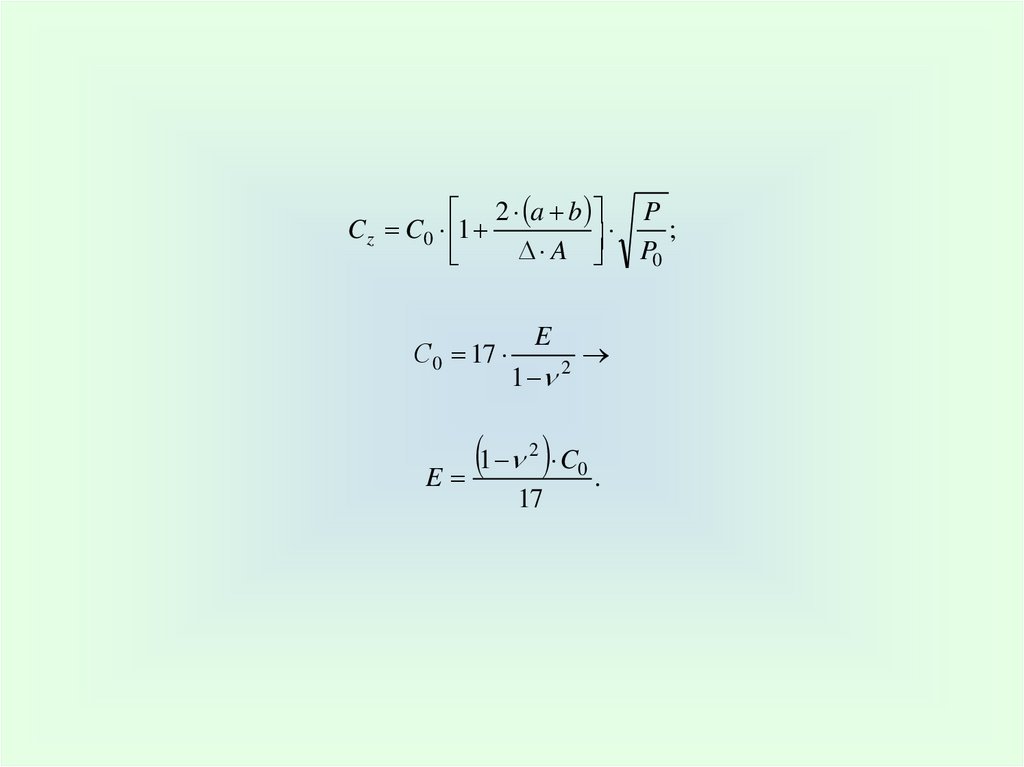

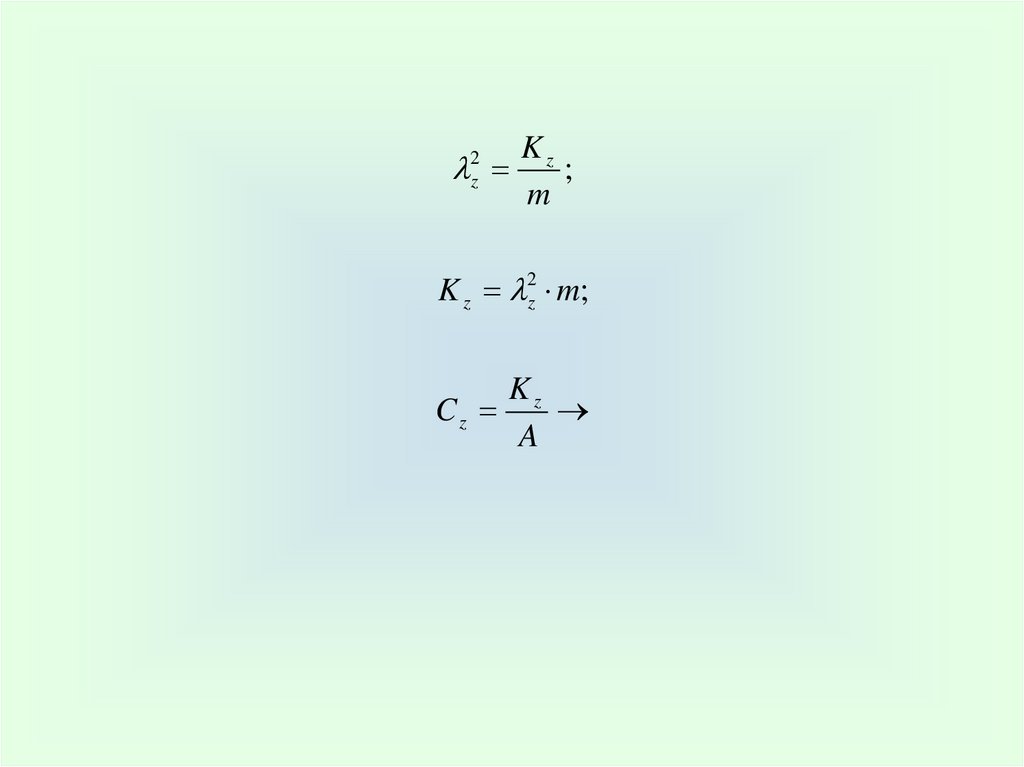
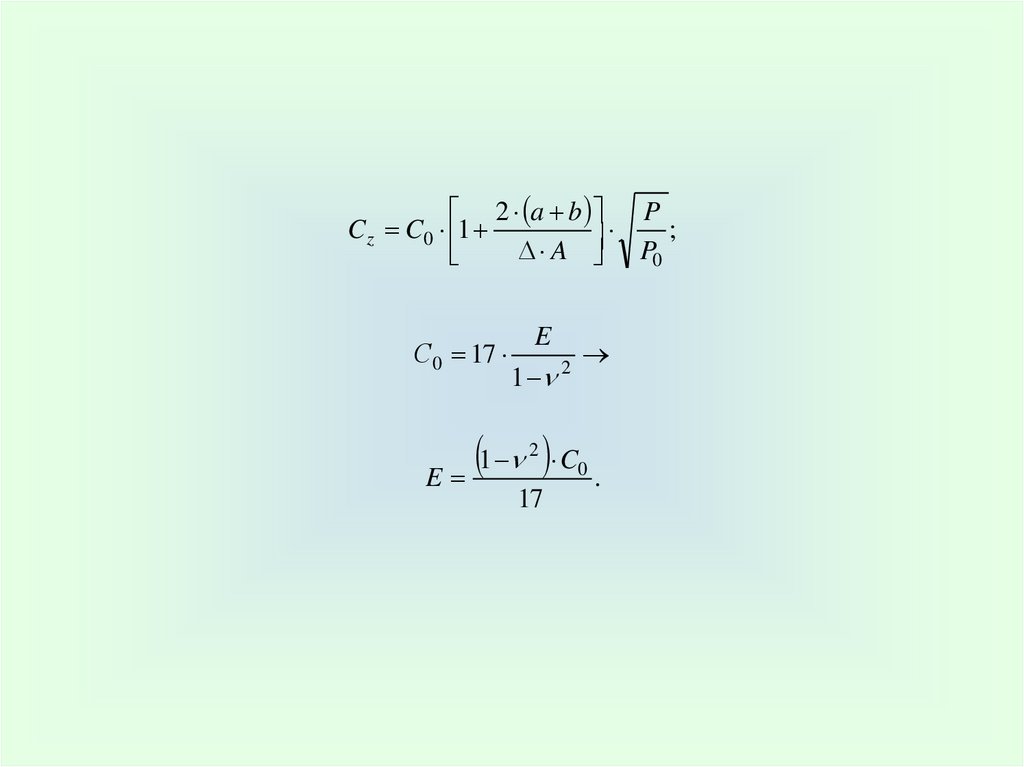




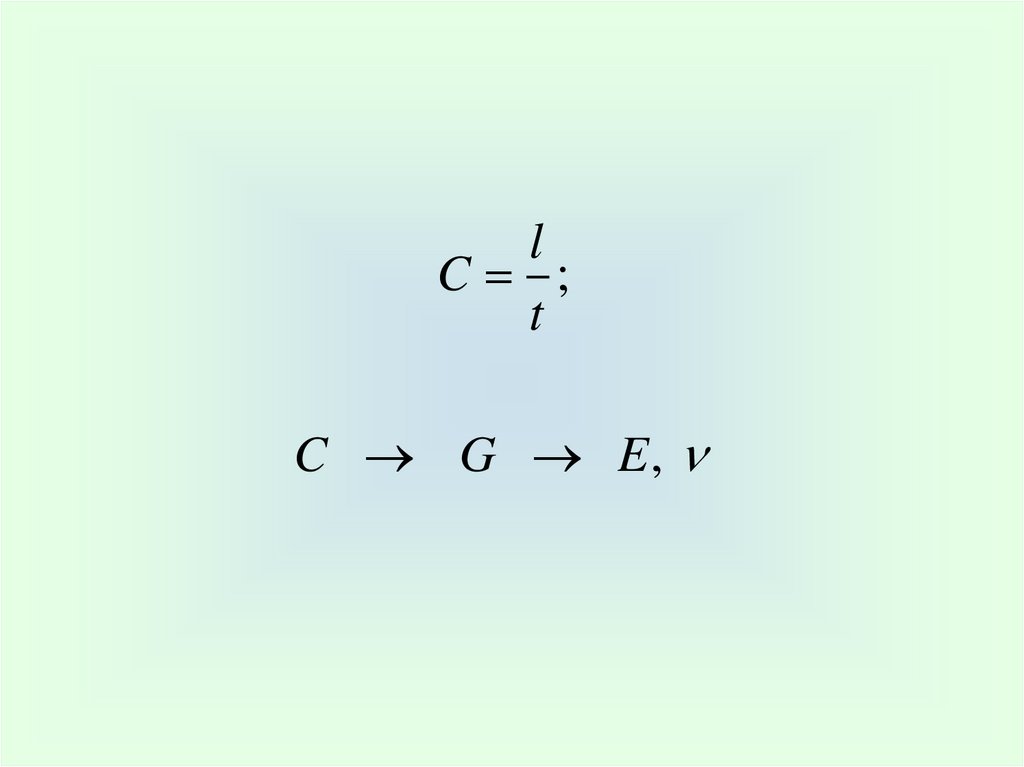


 physics
physics