Similar presentations:
Системы линейных уравнений
1.
2.
Определение 1. Пусть задана системаиз m линейных уравнений с n неизвестными x1,
x2, …, xn:
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2n n
2
.............................................
am1 x1 am 2 x2 ... amn xn bm
(1.1)
где числа aij (i = 1, 2, …, m; j = 1, 2, …, n)
называются коэффициентами системы,
а числа b1, b2, …, bm – свободными членами.
3.
Определение 2. Решением системы (1.1)называется такой набор чисел (c1, c2, …, cn),
что при его подстановке в систему вместо
соответствующих неизвестных (c1 вместо
x1, c2 вместо x2, …, cn вместо xn) каждое из
уравнений
тождество.
системы
обращается
в
4.
Определение 3. Если система (1.1) имеетхотя бы одно решение, она называется
совместной; система, не имеющая ни
одного решения, называется несовместной.
Система называется определенной, если она
имеет
единственное
решение,
и
неопределенной, если она имеет более
одного решения.
5.
ОпределениеДве
4.
системы
линейных
уравнений с одинаковым числом неизвестных
называются
множества
совпадают.
эквивалентными,
всех
решений
этих
если
систем
6.
Определение 5. Если b1 = b2 = … = bm = 0, тосистема
называется
противном
случае
однородной,
она
в
называется
неоднородной.
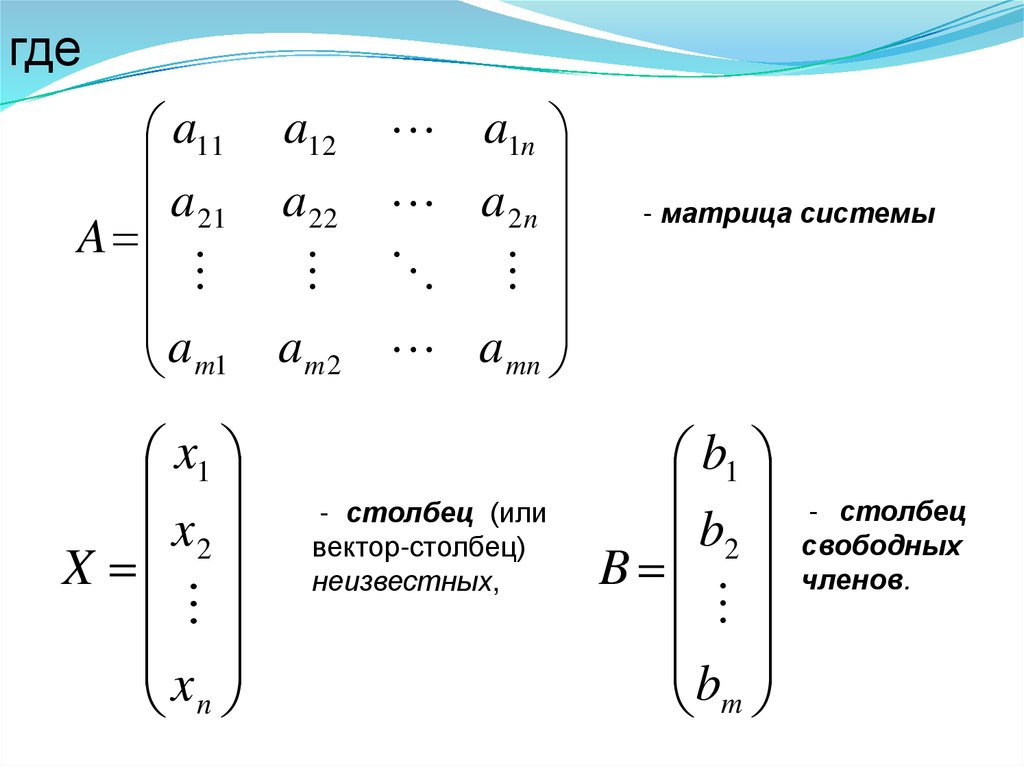
Систему (1.1) можно записать в матричной
форме:
AX=B,
7.
гдеa11
a 21
A
a
m1
x1
x2
X
x
n
a12
a 22
am2
a1n
a2n
a mn
- столбец (или
вектор-столбец)
неизвестных,
- матрица системы,
b1
- столбец
b2 свободных
B членов.
b
m
8.
Определение 6. Матрица называетсярасширенной матрицей системы если она
имеет следующий вид.
a11
a 21
A | B
a
m1
a1n b1
a 2 n b2
a mn bm
9.
Пример 1. Дана система линейных уравнений2 x1 2 x 2 3x3 15
3x1 4 x2 2 x3 4
4 x 6 x 5 x 1
2
3
1
Требуется показать, что система совместна,
и найти ее решение тремя способами: а) по
формулам Крамера; б) методом Гаусса; в)
методом обратной матрицы. Выполнить
проверку решения.
10.
Решение: а) по формулам КрамераСистема n линейных уравнений с n
неизвестными является совместной и имеет
единственное решение, при условии что
определитель системы, составленный из
коэффициентов при неизвестных будет
отличен от нуля. Вычислим определитель
системы методом разложения его по
элементом строки. Разложим по первой
строке:
11.
34
2 2
6
5
2
D 3
4
2
4
6
3
3
4
4
2( 20 12) 2(15 8)
6
3(18 16) 180 0
2
3
2
5
4
2
5
12.
Определитель системы не равен нулю, системауравнений совместна и имеет единственное решение.
Найдем решение системы по формулам Крамера
D2
D1
x1
, x2
D
D
D3
x3
D
где D1 D2 D3 - определители, которые получаются из
определителя D системы путем замены в нем
соответственно
1-го,
2-го,
3-го
столбцов
коэффициентов при неизвестных x1 x2 x3 столбцом
свободных членов уравнений, стоящих в правой
части данной системы. Получим следующие три
определителя:
13.
15 2 34 2
4 2
D1 4 4 2 15
2
6 5
1 5
1 6
5
4 4
3
15( 20 12) 2( 20 2)
1 6
3( 24 4) 360
14.
2 15 34 2
3 2
D2 3 4 2 2
15
1 5
4 5
4 1 5
3 4
3
2( 20 2) 15(15 8)
4 1
3( 3 16) 180
15.
2 2 154 4
3 4
D3 3 4 4 2
2
6 1
4 1
4 6 1
3 4
15
2( 4 24) 2( 3 16)
4 6
15(18 16) 540
16.
Вычислить неизвестные180
360
1 ,
х1
2 , х2
180
180
540
х3
3 .
180
Ответ: 2; 1; −3
17.
Проверим это решение, подставив значениянеизвестных во все уравнения системы.
Получим
2 2 2 1 3( 3) 4 2 9 15
3 2 4 1 2( 3) 6 4 6 4
4 2 6 1 5( 3) 8 6 15 1
Решение верное.
18.
б) Решение системы уравнений методом Гаусса.Для этого выпишем расширенную матрицу
системы и приведем основную матрицу системы к
треугольному виду или ступенчатому виду.
3 15
2 2
2 2 3 15
~
3 4 2 4 I * 3 II * 2 ~ 0 14 13 53
I * 2 III 0 2 11 31 II III * 7
4 6
1
5
2 2 3 15
~ 0 14 13 53
0 0 90 270
19.
Вернемся от матричной записи к системе уравнений.2









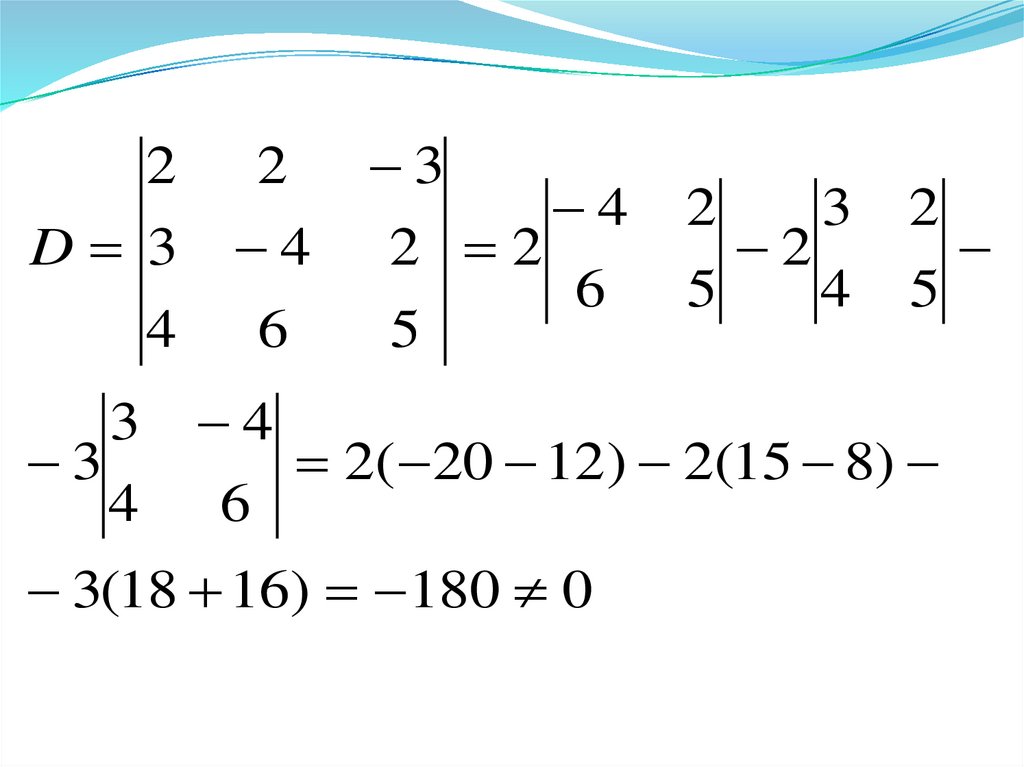

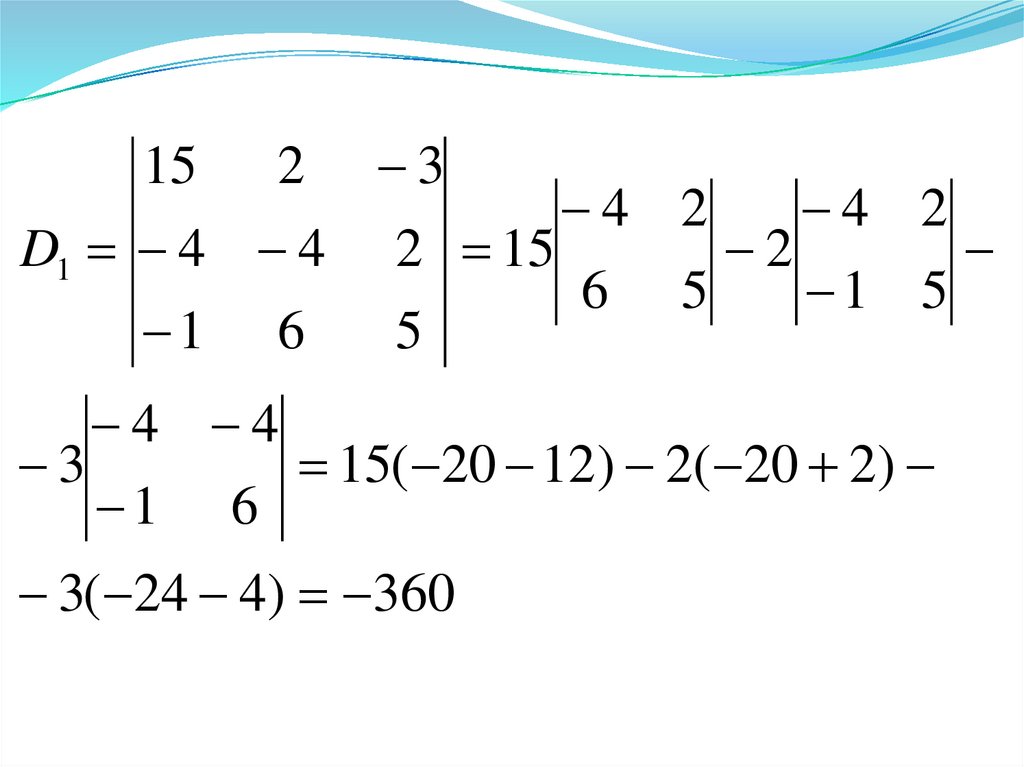
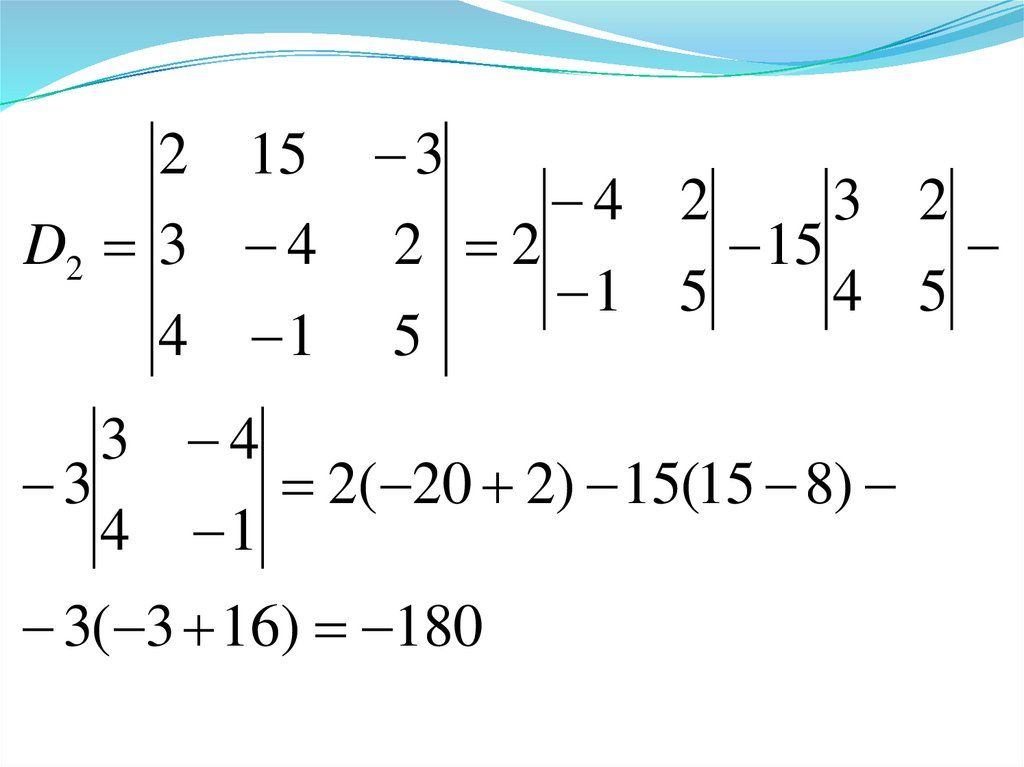
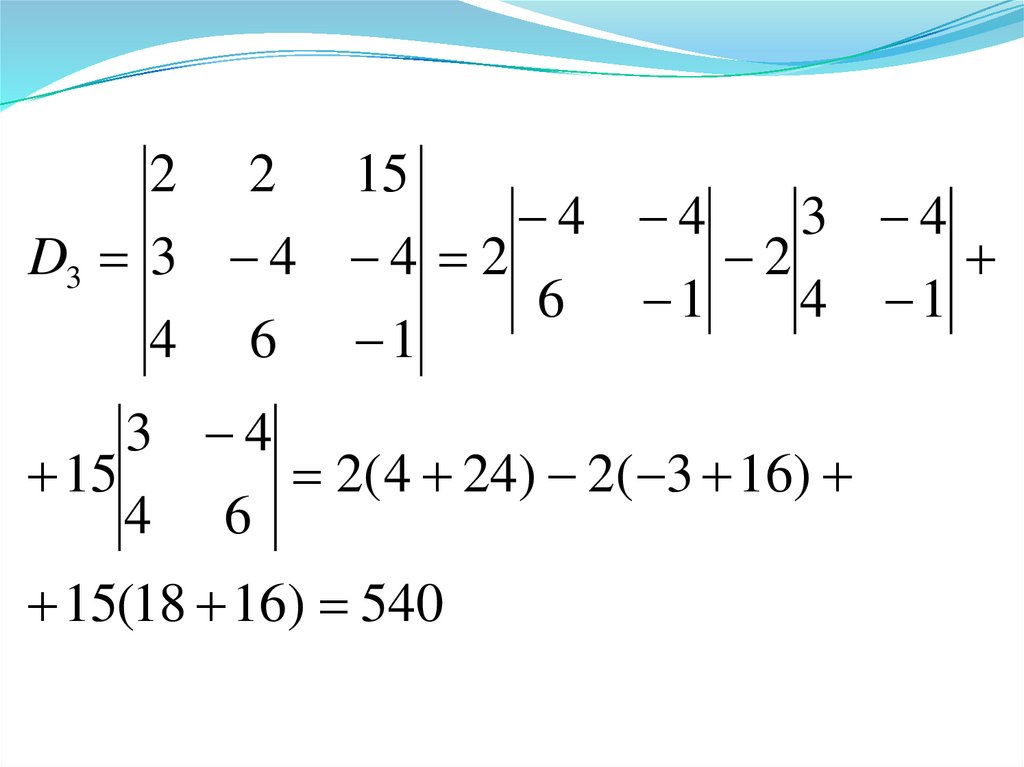









 mathematics
mathematics








