Similar presentations:
Обыкновенные дифференциальные уравнения
1.
Раздел I.ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ (ДУ).
План лекции:
1. §1. ОСНОВНЫЕ ПОНЯТИЯ.
2. §2. ДУ1 . ОБЩЕЕ И ЧАСТНОЕ РЕШЕНИЕ.
3. §3. ДУ1 С РАЗДЕЛЁННЫМИ И РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ.
2.
§1. ОСНОВНЫЕ ПОНЯТИЯ.Рассмотрим физическую задачу.
Постановка задачи:
С высоты сброшено тело массой m.
Требуется установить закон изменения
скорости v падения этого тела, если на
него, кроме силы тяжести, действует
тормозящая сила сопротивления воздуха,
пропорциональная скорости
( коэффициент пропорциональности k ).
3.
Решение:По условию требуется найти функцию v = f(t).
Используем второй закон Ньютона:
a v
dv
,
dt
ma = F (*) , где
F – сила,
действующая на тело.
Fсоп. kv
Fтяж. mg
Тогда
F = mg – kv .
=> (*) перепишем так:
dv
m
mg kv (**).
dt
4.
(**) есть ДУ, связывающее неизвестнуюdv
функцию v и её производную .
dt
Т.о. решение задачи свелось к решению ДУ.
5.
Df1:Дифференциальным уравнением (ДУ) называется равенство, содержащее независимую
переменную х, неизвестную функцию y = f(x) и
её производные и обозначается:
F ( x, y, y , y ,....., y
( n)
) 0 (1.1)
Если y = f(x) – функция одного аргумента, то
ДУ называется обыкновенным, все остальные
уравнения относятся к уравнениям в частных
производных.
6.
Порядок старшей производной в ДУопределяет порядок ДУ .
Пр.1:
y 2 xy 0
ДУ 3 ,
2 x 2 yy 5
ДУ1 ,
1
x cos xy 5 y 7 4
не является ДУ.
7.
Df.2: Решением ДУ называется функцияy = f(x), удовлетворяющая данному ДУ.
§2. ДУ1. ОБЩЕЕ И ЧАСТНОЕ РЕШЕНИЕ.
ДУ 1 имеет вид
F ( x, y, y ) 0
(2.1),
т.е в уравнение ДУ 1 входит аргумент х,
неизвестная функция у и её производная
первого порядка.
8.
Df.1:Искомая функция y = f(x,c) (2.2) , где
c = const называется общим решением (ОР) ДУ 1
Если решение представлено в виде
F(x,y,c)=0 , то такое решение называется
общим интегралом.
9.
С геометрической точки зрения ОР естьсемейство интегральных кривых, отличающихся
друг от друга на константу.
Пр.1:
Показать, что y x c является общим
решением ДУ 1 : y 2 x 0.
2
10.
В ДУ 1 подставим вместо у его значение:2
x c 2 x 0
2x – 2x = 0
0 = 0 – верное равенство.
С геометрической точки зрения ОР уравне2
ния y x c представляет собой семейство
парабол, которые смещены друг от друга по оси
y x 2
y
Оу на константу c:
2
y x2
2
y x2 5
0
x
y x2 5
-5
11.
Df.2:Частным решением (ЧР) ДУ 1 называется
функция y f ( x; c0 ) , которая получается из ОР при
фиксированном значении const c c0 .
С геометрической точки зрения ЧР – это
одна интегральная кривая из семейства интегральных кривых.
12.
Пр.2:y x 2 c – ОР.
y 2 x 0,
Дано:
Найти: ЧР.
Решение:
Пусть с = -1, тогда y x 2 1 – ЧР.
y
y x 2 1
0
-1
x
13.
Решение ДУ 1 рассмотрим на примере.Пр.3:
Пусть дано уравнение : y 2 x 0 (*)
а) Для нахождения ОР (*) выполним операции:
1) выразим производную: y 2 x.
2) проинтегрируем полученное равенство:
y 2 xdx
ДУ 1
или
y x 2 c – ОР данного
14.
б) Для нахождения ЧР используется задача Коши:F ( x , y, y ) 0,
y0 y ( x 0 )
или
M 0 ( x 0 ; y0 )
или
ДУ 1
y x x0 y0 . нач. условия.
M 0 ( x0 , y 0 ) - точка через которую проходит интег-
ральная кривая (частное решение).
Zm.1:
Решить задачу Коши – значит найти ЧР ДУ.
15.
Пр.4: Решить задачу Коши:Решение: y 2 x 0
y 2x 0,
y x 2 4.
y 2 x
y 2 xdx x 2 c.
- OP.
Чтобы найти ЧР надо найти с. Для этого
подставим начальные условия в ОР:
y x2 c
Тогда
4 22 c
y x
- ЧР.
Ответ:
2
c 0
y x .
2
16.
§3. ДУ1 С РАЗДЕЛЁННЫМИ И РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ.Df.1:
ДУ 1 вида P(x)dx + Q(y)dy = 0 (3.1)
называется уравнением с разделёнными
переменными.
Пр.1:
y 2x
dy
2x
dx
dy
Вспомним: y
dx
. dx
dy = 2xdx - уравнение с разделёнными
переменными.
17.
dy 2 xdxy x2 c
- ОР
Df.2:
ДУ 1 вида P1 ( x)Q1 ( y)dx P2 ( x)Q2 ( y)dy 0 (3.2)
называется уравнением с разделяющимися
переменными.
Чтобы решить уравнение (3.2), надо свести
его к уравнению (3.1), разделив обе части уравнения (3.2) на произведение ,, лишних “
множителей.
18.
Пр.2:Решить уравнение dy 2 x y dx 0. (*)
x y
Решение: dy 2 dx 0.
x
y
dy 2 2 dx 0.
dy
x
2
dx 0
y
2
dy
x
2
dx
y
2
dy
x
2
2 y dx
2 y d ( y ) 2 x dx
2 y
2x
c
ln 2 ln 2
: 2y
- Общий интеграл ДУ.
Ответ:
2 y
2x
c.
ln 2 ln 2
19.
Изменим условие задачи, т.е. решим задачу Коши.Для уравнения (*) запишем начальные
условия: у(0) = 0.
Тогда
20
20
c
ln 2 ln 2
2 y
2x
2
ln 2 ln 2 ln 2
⇒
2
c
.
ln 2
- ЧР уравнения (*) .
20.
Правило решения ДУ1 с разделяющимисяпеременными.
Чтобы решить ДУ1 вида (3.2), необходимо:
1. Свести уравнение (3.2) к уравнению (3.1),
разделив обе части уравнения (3.2) на «лишние»
множители.
2. Получившееся уравнение проинтегрировать и
найти общее решение (ОР).
3. Если в задаче указаны начальные условия, то
эти условия надо подставить в общее решение; из
полученного уравнения найти значение константы
с и подставить его в ОР, т.о. получится частное
решение (ЧР) уравнения.











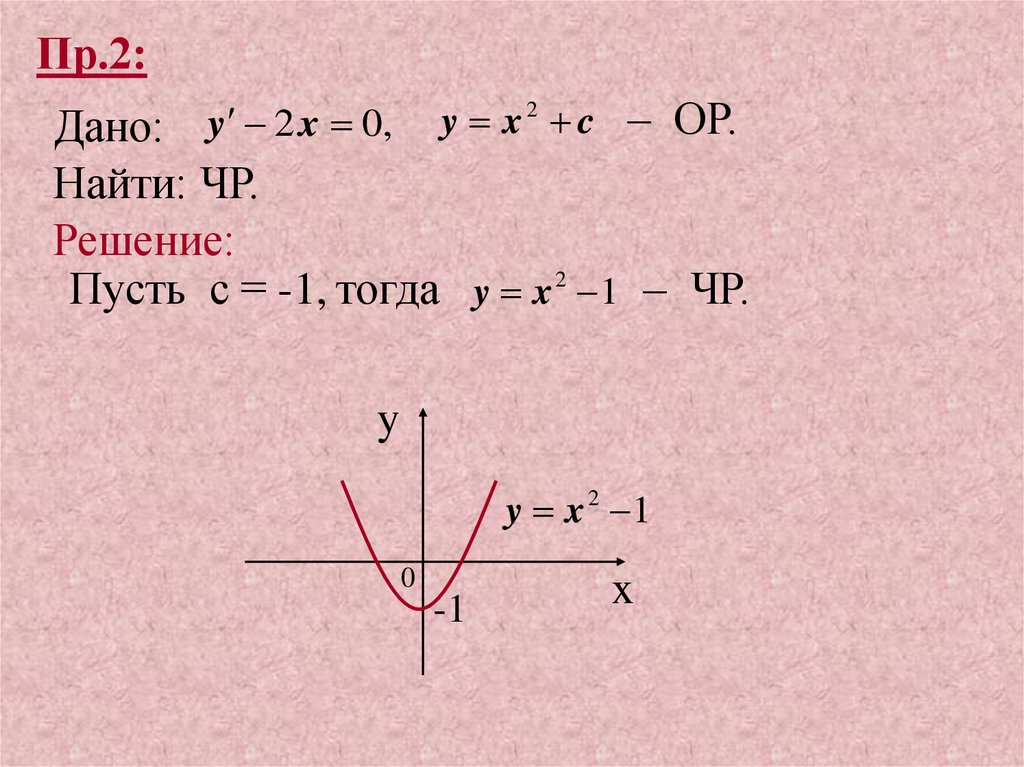








 mathematics
mathematics








