Similar presentations:
Обыкновенные дифференциальные уравнения. Теорема существования. (Лекция 2.7)
1. Лекция 2.7. 12. Обыкновенные дифференциальные уравнения. 12.1. Дифференциальные уравнения 1-го порядка. 12.1.1. Общие понятия. Теорема существовани
Лекция 2.7.12. Обыкновенные дифференциальные уравнения.
12.1. Дифференциальные уравнения 1-го порядка.
12.1.1. Общие понятия. Теорема существования.
Простейшие дифференциальные уравнения: y¢ = f ( x )
или dy = f ( x ) dx.
Решение y = ò f ( x ) dx + C.
Более сложные дифференциальные уравнения:
xy¢ - y = 0,
xy¢ = y + x
и
y¢ + x 2 y = 0,
т.д.
dy + x 2 ydx = 0, xdy - ydx = 0, xdy = ( y + x ) dx
или
и
т.д.
2. Определение.
Дифференциальным уравнением 1-го порядканазывается уравнение, связывающее
независимую переменную x, функцию y, и ее
производную y¢.
Будем рассматривать дифференциальные
уравнения функции одной переменной.
Общий вид дифференциального уравнения 1-го
порядка
F ( x, y, y¢ ) = 0 или y¢ = f ( x, y ) .
3. Определение.
Решением дифференциального уравненияназывается функция, которая при подстановке ее
вместе с производной в это уравнение
превращает его в тождество.
y¢ = y.
y = Ce x .
Примеры: 1)
Решение
где C - произвольная постоянная.
-x
¢
y
=
y
.
y
=
Ce
.
2)
Решение
4. Дифференциальное уравнение 1-го порядка
y¢ = f ( x, y ) .имеет бесчисленное множество решений, которые обычно
определяются формулой
одну
y = j x, Cсодержащей
,
произвольную постоянную. Такое множество решений
называют общим решением дифференциального
уравнения. Придавая
определенные (допустимые)
C
значения, получим частные решения.
При решении конкретных задач нас будет интересовать
частное решение, определяемое начальными условиями.
Обычно начальные
условия задаются парой значений
или
Задача отыскания частного решенияx0по,начальному
y0
y условию
= y0 .
x = xo
называется задачей Коши.
(
)
( ) ( )
5. Теорема Коши о существовании и единственности решения.
y¢ = f ( x, y )Пусть дано дифференциальное уравнение
y x = x = y0 .
и начальное условие
¶f
o
Если функция f ( x, y )и ее частная производная
¶y
непрерывны в открытой области, содержащей точку
P ( x0 , y0 ) ,
то в достаточно малом интервале
( x0 - h, x0 + h ) это уравнение имеет единственное
решение y = y ( x ) , удовлетворяющее заданному
начальному условию ( y ( x0 ) = y0 ) .
Без доказательства.
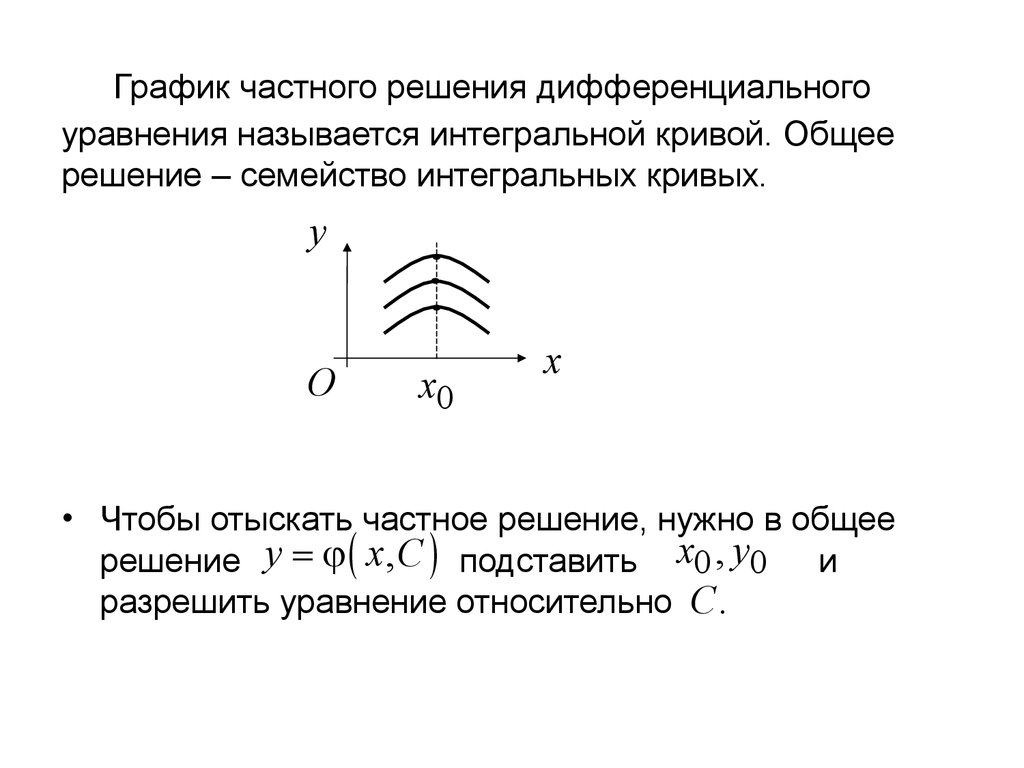
6. График частного решения дифференциального уравнения называется интегральной кривой. Общее решение – семейство интегральных кривых.
yO
x0
x
• Чтобы отыскать частное решение, нужно в общее
решение y = j ( x, C ) подставить x0 , y0
и
разрешить уравнение относительно C.
7. Примеры: 1)
yДифференциальное уравнение y¢ = 2 x.
Общее решение y = x 2 + C.
x
y
=
2.
Начальное условие x =1
Подставим начальное условие в общее решение
дифференциального уравнения. Получим алгебраическое
уравнение для определения произвольной постоянной
2 = 1 + C.
Следовательно C = 1.
Частным решением дифференциального уравнения,
2
удовлетворяющим начальным условиям будет y = x + 1.
8. 2)
yДифференциальное уравнение y¢ = y.
Общее решение y = Ce x .
Начальное условие y x =0 = 2.
Подставим начальное условие в общее решение
дифференциального уравнения. Получим 2 = C.
Частным решением дифференциального уравнения,
удовлетворяющим начальным условиям будет
y = 2e x .
x
9. 3)
Дифференциальное уравнениеy+x
y¢ =
,
x
( x > 0) .
Общее решение y = x ln x + Cx. Начальное условие y x =1 = 0.
Подставим начальное условие в общее решение
дифференциального уравнения. Получим C = 0.
Частным решением дифференциального уравнения,
удовлетворяющим начальным условиям будет y = x ln x.
Общее решение дифференциального уравнения
может быть получено и в неявном виде
Ф ( x, y, C ) = 0.
10. 12.1.2. Дифференциальные уравнения с разделяющимися переменными.
Рассмотрим дифференциальное уравнениеf ( y ) dy = g ( x ) dx.
Проинтегрировав, получим
Если
y x = x = y0 , то
0
Пример:
y
ò f ( y ) dy = ò g ( x ) dx + C.
x
ò f ( y ) dy = ò g ( x ) dx.
y0
x0
3 2
2
3
2
3 y dy = 2 xdx, y = x + C , y = x + C .
11. Определение. Дифференциальные уравнения, в которых переменные можно разделить посредством умножения или деления обеих частей уравнения н
Определение. Дифференциальные уравнения, вкоторых переменные можно разделить посредством
умножения или деления обеих частей уравнения на
одно и то же выражение, называются
дифференциальными уравнениями с разделяющимися
переменными.
dy f ( x )
=
,
dx g ( y )
P ( x ) Q ( y ) dy + M ( x ) N ( y ) dx = 0,
ò g ( y ) dy = ò f ( x ) dx + C.
Q( y)
M ( x)
ò N ( y ) dy + ò P ( x ) dx = C.
Внимание! Может произойти потеря частного
решения.
12. Пример.
Рассмотрим дифференциальное уравнениеx y + 1 dx - x 2 + 1 ydy = 0.
(
)
(
)
Разделим переменные
x
y
æ
1
1 ö
2
dx dy = 0,
ln x + 1 - ò ç1 dy = ln C ,
÷
2
y +1
2
y +1ø
x +1
è
(
(
)
1
ln x 2 + 1 - y + ln y + 1 = ln C ,
2
Потеряли частное решение
)
Ce y
= x 2 + 1.
y +1
y = -1.
13. 12.1.3. Физические задачи, приводящие к дифференциальным уравнениям.
1) Радиоактивный распад. Экспериментально установлено,что скорость распада пропорциональна количеству не
t0
распавшегося вещества. В момент
dM
M = M 0 . dM = - kM ( k > 0 ) ,
= - kdt , ln M = - kt + ln C ,
M
dt
- kt .
kt
M
=
M
e
M
=
M
®
C
=
M
,
M = Ce ,
0
0
0
t =0
M0
- kT ® e kT = 2.
Период полураспада TТогда
=
M
e
.
0
2
Следовательно
ln 2
T=
.
k
k
- определяется экспериментально.
14. 2) Охлаждение тела.
Скорость охлаждения тела пропорциональна разностимежду температурой тела T и температурой
окружающей среды Tc . Tc = const ,
T t = T0 .
0
dT
= - k ( T - Tc ) , ( k > 0 ) ,
dt
dT
= - kdt ,
T - Tc
ln ( T - Tc ) = - kt + ln C , ( T > Tc ) , T = Tc + Ce - kt ,
T t =0 = T0 ® T0 = Tc + C ® C = T0 - Tc .
Окончательно
T = Tc + ( T0 - Tc ) e - kt
15. 12.1.4. Однородные дифференциальные уравнения.
Определение. Дифференциальное уравнениеy¢ = f ( x, y )
называется однородным, если функция f ( x, y ) может быть
представлена, как функция отношения своих аргументов
æ yö
f ( x, y ) = j ç ÷ .
èxø
(
2
y æ yö
-ç ÷
2
dy xy - y
x èxø
2
2
=
=
.
xy - y dx - x - 2 xy dy = 0,
y
dx x 2 - 2 xy
1- 2
x
Пример.
) (
)
16. Функция называется однородной функцией измерения если
Функция f ( x, y ) называется однородной функциейизмерения m, если f lx, ly = l m f x, y .
(
)
(
)
• Примеры: 1) f ( x, y ) = x + 3 y - 1-й порядок
однородности.
f ( lx, ly ) = lx + 3ly = l ( x + 3 y ) = lf ( x, y ) .
f ( x, y ) = x 2 + 4 xy + 5 y 2
2
f ( lx, ly ) = l - f2-й
y) .
( x,порядок
• 2)
однородности.
f ( x, y ) =
• 3)
x2 - y 2
x 2 + 7 xy
- fнулевой
= l 0 f ( xоднородности
, y ) = f ( x, y ) .
( lx, ly )порядок
2
2
2
(просто однородная функция)
1- ( y / x)
x -y
f ( x, y ) = функции.
=
• Пример приведения
2
y 2 + xy
( y / x)
æ yö
= jç ÷
èxø
+ y/x
17. Дифференциальное уравнение где однородная функция нулевого измерения, можно преобразовать к уравнению с разделяющимися переменными.
y¢ = f ( x, y ) ,f ( x, y )
Дифференциальное уравнение
где
однородная функция нулевого измерения, можно
преобразовать к уравнению с разделяющимися
переменными.
• Введем вспомогательную функцию t = y / x или y = tx.
y¢ = t ¢x + t.
dt
dx
= ,
• Тогда t ¢x + t = j ( t ) , t ¢x = j ( t ) - t ,
j( t ) - t
x
dt
ò j ( t ) - t = ln x + C.
• Вычислив интеграл, и перейдя к y = tx, получим
F ( x, y ) = ln x + C.
• Предполагается, что j ( t ) - yt ¹ 0.
¢
• Если j ( t ) - t º 0, то y = x - C.
18. Пример.
y = tx,y¢ = t ¢x + t ,
y¢ =
xy - y
2
x 2 - 2 xy
t - t2
t ¢x + t =
,
1 - 2t
1 - 2t
dx
Тогда
dt = .
x
t2
.
dt 1 æ t - t 2 ö 1 t 2
= ç
-t÷ =
.
dx x çè 1 - 2t ÷ø x 1 - 2t
1
C
+ 2ln t = ln
Проинтегрировав, получим
t
x
или
C
C
1/
t
2
1/
t
2
ln e t = ln
®e t = .
x
x
Окончательно
y2 x / y
e
= C.
x

















 mathematics
mathematics








