История возникновения геометрии

1.

„Более
важно,
что
геометрия
есть
феномен
общечеловеческой
культуры.
История
геометрии
отражает историю развития человеческой мысли,
а некоторые теоремы геометрии являются одними
из древнейших памятников мировой культуры. Человек
не может по-настоящему развиться культурно и духовно,
если он не изучал геометрию.“
И.Ф. Шарыгин, российский математик и педагог,
популяризатор науки 1937–2004

2. Список основной литературы

1. Д.В. Беклемишев. Курс аналитической геометрии
и линейной алгебры.(учебник) инженерный поток
2. Под редакцией А.В. Ефимова, Б.П. Демидовича.
Сборник задач по математике, часть1.
инженерный поток
3. О.Н. Цубербиллер. Задачи и упражнения по
аналитической геометрии.
4. Ильин В.А., Позняк Э.Г. Аналитическая
геометрия. Учебник для вузов.
5. Ильин В.А., Позняк Э.Г. Линейная алгебра.
Учебник для вузов.
6. Л.А. Беклемишева. Сборник задач по
аналитической геометрии и линейной алгебре.

3.

Список дополнительной литературы
1. А.Н. Канатников, А.П. Крищенко.
Линейная алгебра. (учебник).
2. А.Н. Канатников, А.П. Крищенко.
Аналитическая геометрия. (учебник).
3. Д. Письменный.
Конспект лекций по высшей математике.

4.

«В математике нет символов для неясных мыслей.»
Кванторы, обозначения и сокращения

5.

История
возникновения геометрии
Геометрия с практической точки зрения - это
потребность измерять формы. Считается, что геометрия
впервые стала важной, когда Египетский фараон хотел
обложить налогом фермеров, которые выращивали
урожай вдоль реки Нил. Чтобы вычислить правильную
сумму налога, люди фараона должны были измерить
количество обрабатываемой земли.

6.

Около 2900 лет до нашей эры
была
построена
первая
египетская пирамида. Знание
геометрии было необходимо
для
построения
пирамид,
которые
состояли
из
квадратного
основания
и
треугольных граней.
Самая ранняя запись формулы для вычисления
площади треугольника датируется 2000 годом до
нашей эры. Египтяне и вавилоняне разработали
практическую геометрию для решения повседневных
проблем, но нет никаких доказательств того, что они
логически выводили геометрические факты из
основных принципов.

7.

История развития геометрии
Геометрия - одна из древнейших отраслей
математики. Геометрические тела были известны
задолго до того, как были выведены математические
принципы.
Геометрия
это
математическое
исследование точек, линий, плоскостей, замкнутых
плоских фигур и твердых тел. Используя это, можно
описать или построить каждый видимый и невидимый
предмет.
Геометрия происходит от слова "geo" - земля,
"metria" - мера. Геометрия возникла как область
знаний,
занимающаяся
пространственными
отношениями. Геометрия одна из двух областей
математики, вторая - арифметика, или алгебра.

8.

Именно
греки
600
–
400 лет до нашей эры
разработали
принципы
современной геометрии.
Фалес Милетский изучил
подобные треугольники и
написал
доказательство
того, что соответствующие
стороны
подобных
треугольников
пропорциональны.
Фалес Милетский греческий философ

9.

Пифагор
(569−475569−475 лет до н. э.)
Пифагор
был
первым
математиком,
логически
выводящим
геометрические
факты из основных принципов.
Пифагор основал братство под
названием
"пифагорейцы",
которые преследовали знания в
математике, науке и философии.
Некоторые
люди
считают
пифагорейскую школу местом
рождения разума и логической
мысли. Наиболее известным и
полезным
вкладом
пифагорейцев была теорема
Пифагора. Теория гласит, что
сумма
квадратов
катетов
прямоугольного
треугольника
равна квадрату гипотенузы.

10.

Он
считается
“отцом
современной
геометрии”. Он
ввел математическую
строгость и аксиоматический метод, все
еще используемый сегодня. Его книга
“Начало”, написанная около 300 лет до
нашей
эры,
считается
самым
влиятельным учебником всех времен и
народов. Книга "Начало" была известна
всем образованным людям на западе до
середины
20-го
века.
Он
предложил 2323 определения,
55 постулатов и 55 аксиом.
Аксиома - это утверждение, которое
принимается без доказательств. Как
только
он
доказал
свое
первое
утверждение, на его основе он доказал
второе, затем третье и т. д. Этот процесс Евклид Александрийский
известен как аксиоматический подход. (325−265325−265 лет до н. э.)
Элементы Евклида составляют основу
современной
геометрии,
которая преподается сегодня в школах,
колледжах и университетах.

11.

Рене́ Дека́ рт
1596−1650
Рене Декарт больше известен
как великий философ, чем
математик.
До
его
появления
в геометрии не
было крупных изменений. Он
объединил
алгебру
и
геометрию
для
создания
аналитической геометрии. АГ,
также
известная
как
координатная
геометрия,
включает
размещение
геометрической
фигуры
в
системе
координат
для
иллюстрации доказательств и
получения
информации
с
использованием
алгебраических уравнений.

12.

Никола́й Ива́ нович
Лобаче́вский
—
русский математик,
один
из
первооткрывателей
неевклидовой
геометрии, деятель
университетского
образования
и
народного
просвещения.

13.

Карл Фридрих Гаусс
(1777−1855)
Следующее
большое
развитие
в
геометрии
пришло
с
развитием
неевклидовой
геометрии.
Карл
Фридрих
Гаусс
изобрел
неевклидову
геометрию, не основанную
на постулатах Евклида.
Параллельный
постулат
гласит, что через заданную
точку на прямой есть одна
и только одна прямая,
параллельная этой линии.
Неевклидова
геометрия
задала
математическую
основу
для
теории
относительности
Эйнштейна.

14.

Французский математик, один
из создателей аналитической
геометрии, математического
анализа, теории вероятностей
и теории чисел. По профессии
юрист, с 1631 года —
советник парламента в
Тулузе. Блестящий полиглот.
Наиболее известен
формулировкой Великой
теоремы Ферма.
Пьер де Ферма́
17 августа 1601 — 12 января 1665

15.

Ирландский
математик,
механик-теоретик,
физиктеоретик, «один из лучших
математиков
XIX
века».
Известен фундаментальными
открытиями в математике
(кватернионы,
основы
векторного
анализа,
вариационное
исчисление,
обоснование
комплексных
чисел),
аналитической
механике
(гамильтонова
механика) и оптике
Уи́ льям Ро́ уэн Га́ мильтон
4 августа 1805 — 2 сентября 1865

16.

Английский математик.
Большое количество его работ
относится к линейной
алгебре, дифференциальным
уравнениям и эллиптическим
функциям. В результате он
смог привести доказательство
теоремы Кэли-Гамильтона о
том, что каждая квадратная
матрица является корнем
своего характеристического
многочлена.
А́ртур Кэ́ ли
16 августа 1821, — 26 января 1895

17.

Французский математик, член
Парижской академии наук
(1885). Имеет труды по
геометрии, комплексному
анализу. Исследовал
ортогональные многочлены .
Эдмо́ н Никола́ Лаге́рр
9 апреля 1834-14 августа 1886

18.

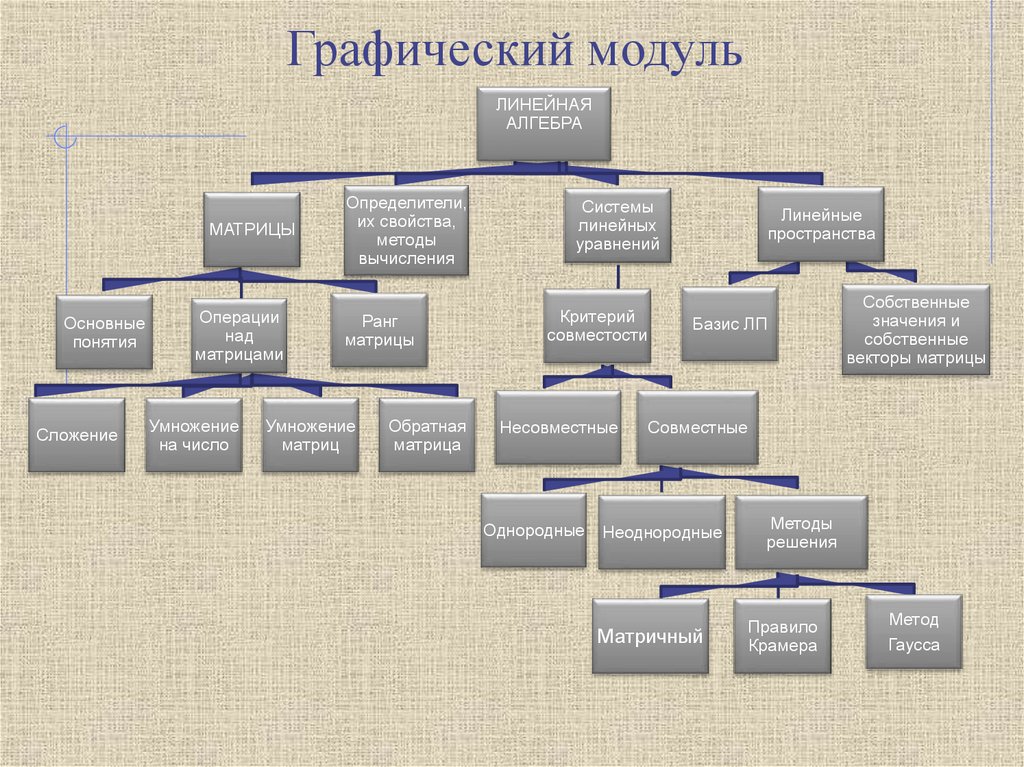
Графический модуль
ЛИНЕЙНАЯ
АЛГЕБРА
МАТРИЦЫ
Основные
понятия
Сложение
Операции
над
матрицами
Умножение
на число
Определители,
их свойства,
методы
вычисления
Ранг
матрицы
Умножение
матриц
Обратная
матрица
Системы
линейных
уравнений
Критерий
совместости
Несовместные
Однородные
Линейные
пространства
Базис ЛП
Собственные
значения и
собственные
векторы матрицы
Совместные
Неоднородные
Матричный
Методы
решения
Правило
Крамера
Метод
Гаусса

19. Основы линейной алгебры

Матрицы. Основные понятия.
Действия над матрицами

20. Матрицы. Основные понятия

Матрицей называется прямоугольная таблица, составленная
из каких – либо элементов и имеющая m строк и n столбцов.
Элементами матрицы могут быть числа, алгебраические
выражения, функции и т.д.
a11
a 21
A
a
m1
a12 ... a1n
a 22 ... a 2n
или
am 2 ... amn
a11
a
21
A
am1
a12
a22
am 2
a1n
a2 n
... amn
...
...
Матрицы обозначаются заглавными буквами латинского алфавита,
элементы матрицы –маленькими буквами латинского алфавита.
Размерность матрицы обозначается:
dim A m n
количество
количество
строк столбцов

21.

Обозначение матриц
a11
a
A 21
am1
a12
a22
am 2
a1n
a2 n
amn
a11
a
21
A
am1
a12
a22
am 2
a1n
a2 n
... amn
...
...
B (bij ) bij bij
A ( aij ) ( i 1, m , j 1, n ) прямоугольная, m n
A ( aij ) ( i, j 1, n )
квадратная порядка n
Матрицы называются однотипными, если они одного
размера.

22.

a11
a
A 21 ( ai1 ) размера m 1
матрица – столбец длины m a
m1
матрица, содержащая один столбец
A a11 a12 a1n (a1 j ) размера 1 n
матрица – строка длины n матрица, содержащая одну строку
0
0
0
0
0
0
0
0
0
нулевая матрица -матрица,
состоящая из нулей.

23. Матрицы. Основные понятия

Если m n , то матрица называется прямоугольной.
Если m n
порядка).
, то матрица называется
квадратной (n - ного
Главная диагональ квадратной матрицы — диагональ, которая
проходит через верхний левый и нижний правый углы. Элементы
главной диагонали называют диагональными
Побочная диагональ квадратной матрицы – диагональ, идущая из
левого нижнего угла в правый верхний угол.
Понятия диагонального элемента и главной диагонали
распространяют и на прямоугольные матрицы.

24.

Квадратная матрица, в которой все элементы, кроме
элементов
главной
диагонали,
равны
нулю,
называется диагональной (разряженной, когда
количество нулей преобладает).
Диагональная матрица, в которой каждый элемент
главной диагонали равен единице, называется
единичной.
a11 0 0
0 a 0
22
диагональная матрица
A
0 0 ann A diag(a11 , a22 , , ann )
1 0 0
0 1 0
E=
единичная матрица
0 0 1

25.

Треугольной
матрицей
называется
квадратная
матрица, в которой элементы, расположенные по одну
сторону от главной диагонали, равны нулю.
a01n
ba1111 a012 a013
b0 ba a0
a
02 n
22
23
21
22
A
B b31
0 b32
0 ba3333
a03 n
b0 b 0 b 0
a
bnnnn
n1 n2 n3
Верхние
Нижние треугольные
треугольные
матрицы,
матрицы, уу которых
которых
элементы,
элементы,
расположенные
под
расположенные
над
главной
диагональю,
главной
диагональю,
равны
равны нулю
нулю
a11 a12
0 a
22
A 0 0
0 0
a1n
a2 n
a3 n
amn
a13
a23
a33
0
a1m
a2 m
a3 m
amm
трапециевидная матрица

26.

Замечание.
Диагональные
матрицы
являются
частным случаем как верхних, так и нижних
треугольных матриц. Множество диагональных матриц
совпадает с пересечением множества верхних
треугольных
матриц
и
множества
нижних
треугольных матриц.
Квадратная матрица называется симметричной (или
симметрической), если элементы, расположенные
симметрично относительно главной диагонали, равны,
т.е. если aij a ji .
Квадратная матрица называется кососимметричной
(антисимметричной), если aij a ji .

27.

Прямоугольную матрицу размера
будем
m n
называть ступенчатой, если первый ненулевой
элемент каждой следующей строки находится правее
первого ненулевого элемента предыдущей строки.
1
0
0
0
2
1
0
0
3
2
1
0
4
3
2
0
5
4
3
0
6
5
4
0
– ступенчатая
1
0
0
0
2
1
1
0
0
2
2
1
0
0
0
2
– не является
ступенчатой
Матрицы называются равными, если они имеют одинаковую
размерность и их соответствующие элементы равны.
A B
dim A dimB;
aij bij

28.

Пример. Назовите виды матриц и их
размерность
1 2 4 6
0 0 1 0
0 2 0 2
x
0
2
0
2
y
1 2 4 6
0 3 5 6
0 0 2 0
0 0
0 0
0 0
1 2
1 0 7 1 0 0
2 2 1 0 1 0
3 2 5 0 0 1
9 0 1
2
1
0
9

29.

Действия над матрицами
Линейные:
1) сложение (вычитание) матриц;
2) умножение матрицы на число.
Нелинейные:
1) Транспонирование матрицы;
2) Умножение матриц;
3) Нахождение обратной матрицы.

30. Действия над матрицами

Сложение (вычитание) матриц
Сумма и разность матриц существуют только для матриц
одинакового размера (однотипных), при этом соответствующие
элементы матриц складываются или вычитаются.
C A B
dim A dim B dim C
cij aij bij

31. Действия над матрицами

Умножение матрицы на число
При умножении матрицы A на число k получается матрица того же
размера, при этом каждый элемент матрицы A умножается на k.
B k A
dim A dim B; bij k aij
Найти значение выражения: C A 5 B
1 3 2
A
0 1 4
2 4 1
B
5 0 2
3 5 ( 4) 2 5 1 11 17 7
1 5 2
C
0 5 ( 5) 1 5 0 4 5 2 25 1 14

32. Действия над матрицами

Свойства операции сложения матриц и умножения матрицы на
число:
1) A B B A; коммутативность
2)
A B C A ( B C ); ассоциативность
3) A O A;
A A O;
Матрица - А =(-1)А называется противоположной к матрице А.
A 1 A; умножение матрицы на единицу не меняет ее
5) A B A B ;умножение матрицы на число дистрибутивно
относительно суммы матриц
6) A A A;
7) A A.умножение матрицы на число ассоциативно
4)

33. Действия над матрицами

Умножение матриц «строчка на столбец»
Произведение матриц A * B определено только тогда, когда
число столбцов матрицы А равно числу строк матрицы В, в
противном случае произведение не существует.
dim A m n
dim B n k
C A B существует
dimC m k
Произведением матрицы A размера [m n] с элементами aij
на матрицу B размера [n k ] с элементами bjq называется
матрица C размера [m k ] с элементами:
n
c iq aij b jq
j 1

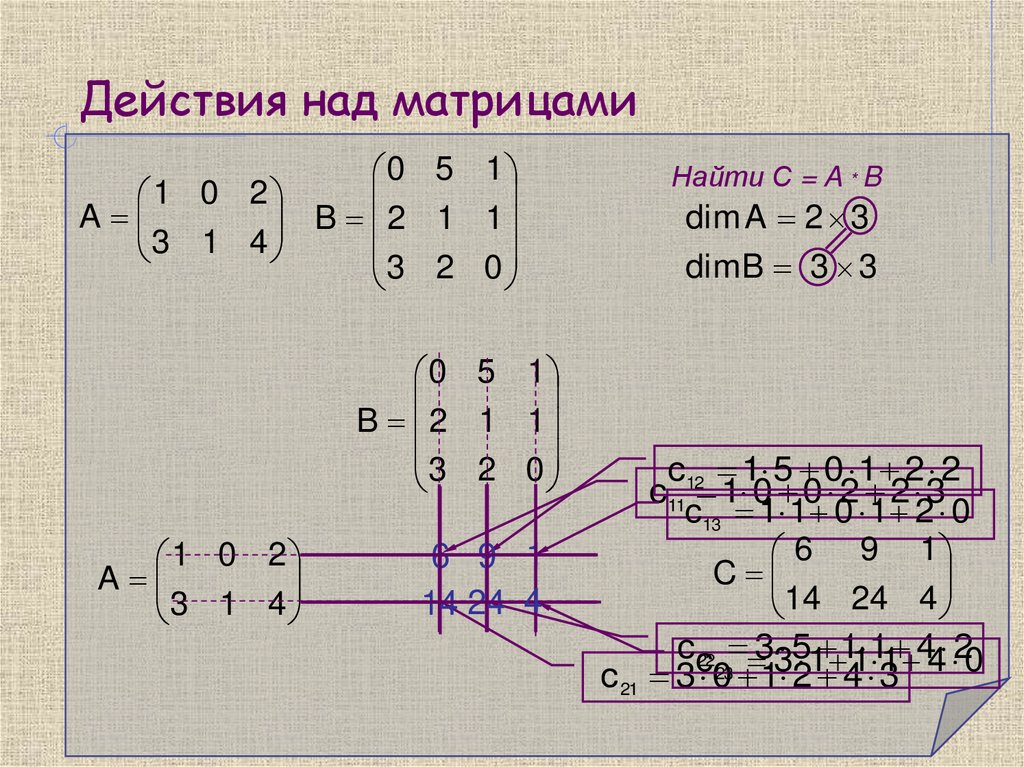
34. Действия над матрицами

1 0 2
A
3 1 4
0 5 1
B 2 1 1
3 2 0
0 5 1
B 2 1 1
3 2 0
1 0 2
A
3 1 4
6 9 1
14 24 4
Найти С = A * B
dim A 2 3
dim B 3 3
c12 1 5 0 1 2 2
c11 1 0 0 2 2 3
c13 1 1 0 1 2 0
6 9 1
C
14 24 4
cc22 33 5 1 11 1
44 20
1
c 21 3 023 1 2 4 3

35. Действия над матрицами

Свойства операции произведения матриц:
ассоциативность
2) AB A B ;
3) A B C AC BC ; С A B СA СB ;
1) A BC AB C ;
4) В общем случае для произведения матриц не действует
переместительный закон: A B B A
иногда АВ существует, а ВА не имеет смысла. В случае, когда
АВ = ВА, матрицы А и В называются коммутативными
(перестановочными).
5) Единичная матрица является коммутативной
квадратной матрицы того же порядка:
EA AE A
для
любой

36. Действия над матрицами

Произведение двух диагональных матриц является
диагональная матрица, причем её элементы являются
результатом произведения диагональных элементов
сомножителей.
diag (a11 , a22 ,
, ann ) diag (b11 , b22 ,
, bnn ) diag (c11 , c22 ,
, cnn )

37.

Действия над матрицами
Операция умножения матриц позволяет ввести
операцию возведения квадратной матрицы в
натуральную степень. Положим
A A,
1
n 1
A
A A, n
n
Введем нулевую степень квадратной матрицы, полагая
A E
0
где Е – единичная матрица того же порядка, что и
матрица А.
Если задан многочлен f ( x) an x n an 1 x n 1 a1x a0 , то
матричным многочленом называется выражение
f ( A) an An an 1 An 1
a1 A a0 A0
Значением матричного многочлена является матрица.

38.

Пример.
Найти значение матричного многочлена, если
f ( x) 3 x 4 x 5,
2
0 2
A
1 1

39.

Умножение матриц «строчка на столбец»
Пусть A – матрица размера m n .
Матрица размера n m , полученная из A заменой
каждой ее строки столбцом с тем же номером,
называется транспонированной к A.
A аij a ji , i 1, m, j 1, n
T
T
Операция
нахождения матрицы
транспонированием матрицы A.
1. (AT)T= A
2. (A+B)T= AT+BT
3.
( A ) A
4.
( A B )T BT AT
T
T
AT
называется

40.

T
A
A , то матрицу А называют симметрической ,
Если
T
если A A - кососимметрической.
Пример.
1 2
2 3
0 2
2 0
и
и
3 2 1
2 0 4
1 4 2
симметрические
0 2 1
2 0 4
1 4 0
кососимметрические

41.

Пример.
2
A 0
4
A
T
3
1
4 , B
0
9
?
2 0 4
A
3 4 9
T
B
2
3
T
?
1 0
B
2 3
T

42. Элементарные преобразование над матрицами:

1. перестановка строк (столбцов);
2. умножение строки (столбца) на число,
отличное от нуля;
3. прибавление к элементам одной строки
(столбца) соответствующих элементов
другой строки (столбца).
Две
матрицы
А
и
В
называются
эквивалентными, если одна из них получается
из
другой
с
помощью
элементарных
преобразований.
A B
Записывается

43.

Матрица, у которой в начале главной
диагонали стоят подряд несколько единиц, а
все остальные элементы равны нулю,
называется канонической.
Замечание:
При помощи элементарных преобразований
любую
матрицу
можно
привести
к
эквивалентной
её
ступенчатой
или
канонической.

44.

Пример.
Привести матрицу к ступенчатому виду с
помощью элементарных преобразований.
1 2 1 1
C 2 3 2 4
4 5 4 6