Решение уравнений математической физики методом д’Аламбера

1. Решение уравнений математической физики методом д’Аламбера

2.

16.24 Найти решение уравнения:
u u
''
tt
''
xx
x
удовлетворяющее начальным условиям:
sin x
u |t 0
x
'
ut |t 0 0

3.

План решения:
1. Определяем тип уравнения.
2. Исходя из начальных условий и формулы Д’Аламбера,
определяем функции ϕ(x) и ψ(x).
3. Получаем решение уравнения u(x,t).
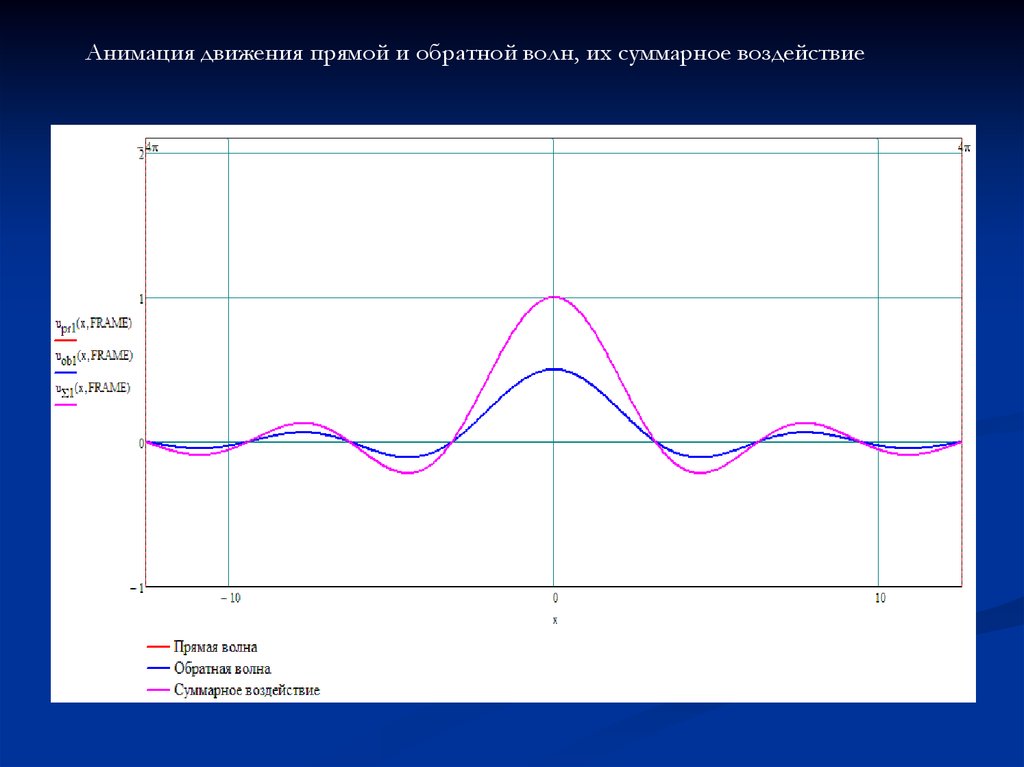
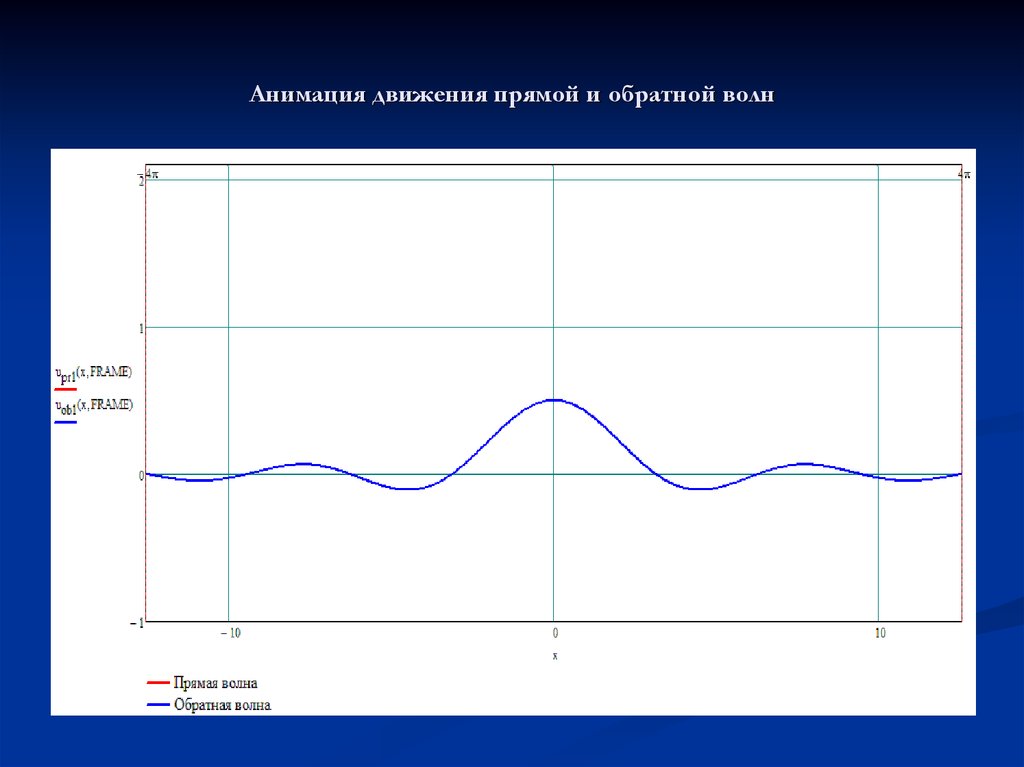
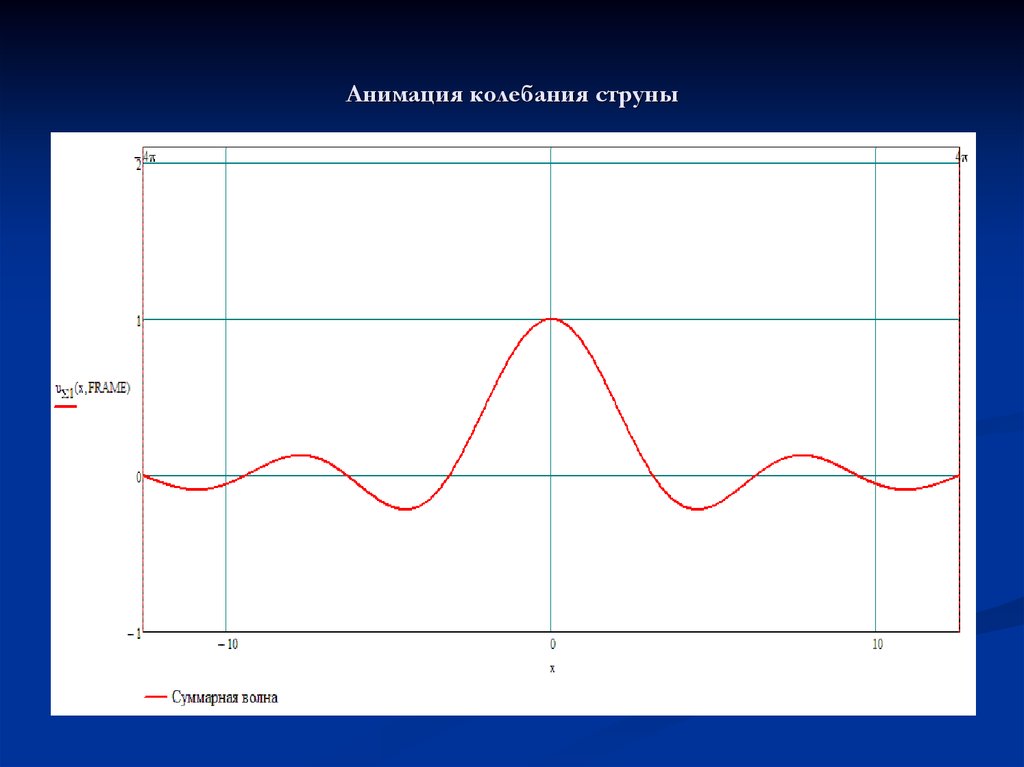
4. Строим графики прямой и обратной волн, а также их
суммарного воздействия для различных моментов времени t.

4.

Решение
1. Приведем уравнение к следующему виду:
где a=1, b=0, c=-1
- уравнение гиперболического типа
Т.е. мы имеем задачу Коши для однородного
(поскольку отсутствует внешняя среда) волнового уравнения.
2. Уравнение Д’Аламбера имеет следующий вид:

5.

Определим функции ϕ(x) и ψ(x).
( x) u |t 0
( x) u |
'
t t 0
=>
sin x
( x)
x
( x) 0
Воспользуемся указанной ранее формулой Д’Аламбера,
подставив в нее заданные функции (учтем, что а = 1):
1
1
u ( x, t ) ( x at ) ( x at )
2
2a
x at
( )d
x at
sin x
x
1 sin( x t ) sin( x t )
( x) 0
2
x t
x t
a 1
( x)
1
2
sin x cos t cos x sin
sin x cos t cos x sin t
x
t
x t
t

6.

1 sin x cos t cos x sin t sin x cos t cos x sin t
u ( x, t )
2
x t
x t
1 ( x t )(sin x cos t cos x sin t ) ( x t )(sin x cos t cos x sin t )
2
2
2
x t
1
2 x sin x cos t 2t cos x sin t
2
2
2( x t )
x sin x cos t t cos x sin t
x2 t 2

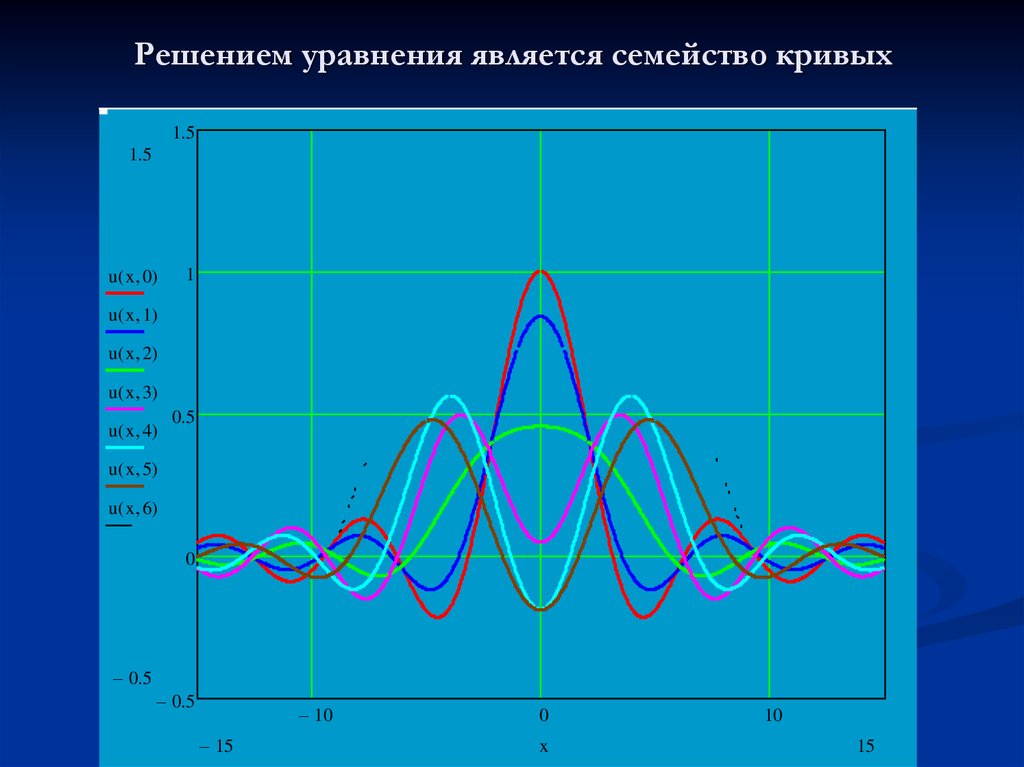
7. Решением уравнения является семейство кривых

1.5
1.5
u( x 0)
1
u( x 1)
u( x 2)
u( x 3)
u( x 4)
0.5
u( x 5)
u( x 6)
0
0.5
0.5
10
15
0
x
10
15

8.

Анимация движения прямой и обратной волн, их суммарное воздействие

9. Анимация движения прямой и обратной волн

10. Анимация колебания струны