Решение уравнений методом «Мини-максов»

1. Решение уравнений методом «Мини-максов»

Применение свойств функций для
решения уравнений
Подготовка к ЕГЭ
Все права защищены. Copyright с 2010. http://www.mathvaz.ru
Copyright с

2. Оглавление

Исследование функции элементарными методами
Метод мини-максов
- уравнение
1
x
х 2 sin
х
2
- уравнение
х 2 2 х 2 cos2 x 1 sin 5 x
- уравнение
х 2 6 х 12 3 sin
3
- уравнение
x 3 sin
3
log3 х 2 2 х 10 х 2 2 х 2 3
Закрыть
x

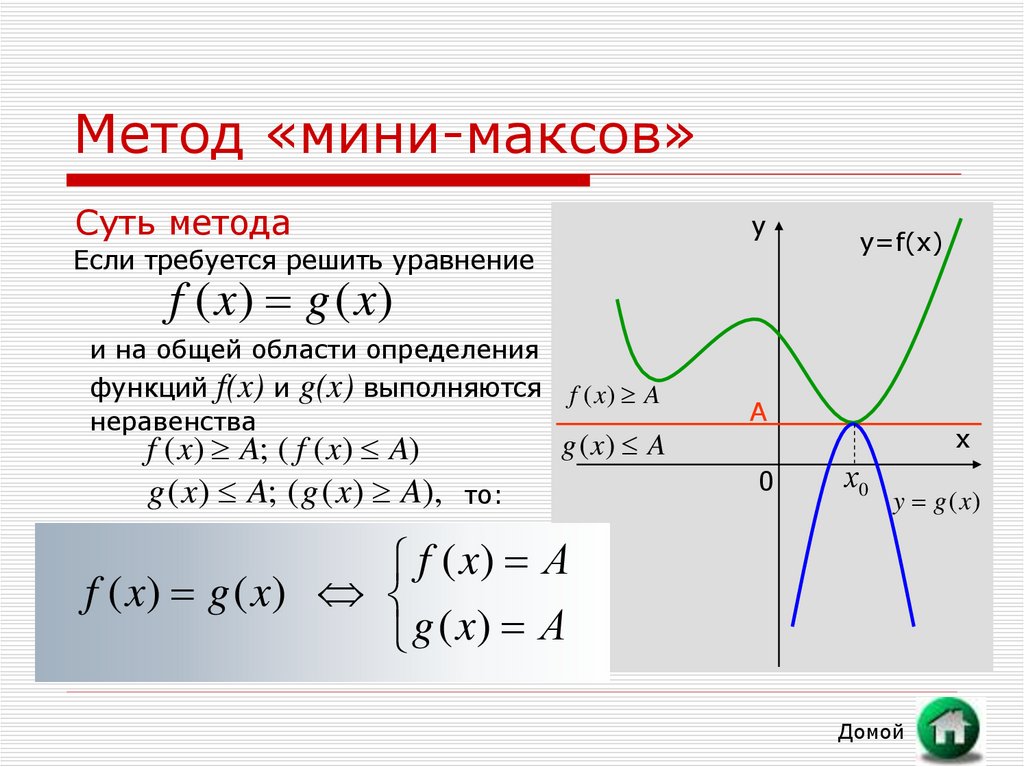
3. Метод «мини-максов»

Суть метода
у
Если требуется решить уравнение
y=f(x)
f ( x) g ( x)
и на общей области определения
функций f(x) и g(x) выполняются
неравенства
f ( x) A; ( f ( x) A)
g ( x) A; ( g ( x) A),
f ( x) A
g ( x) A
то:
A
0
х
х0
y g (x)
f ( x) А
f ( x) g ( x)
g ( x) А
Домой

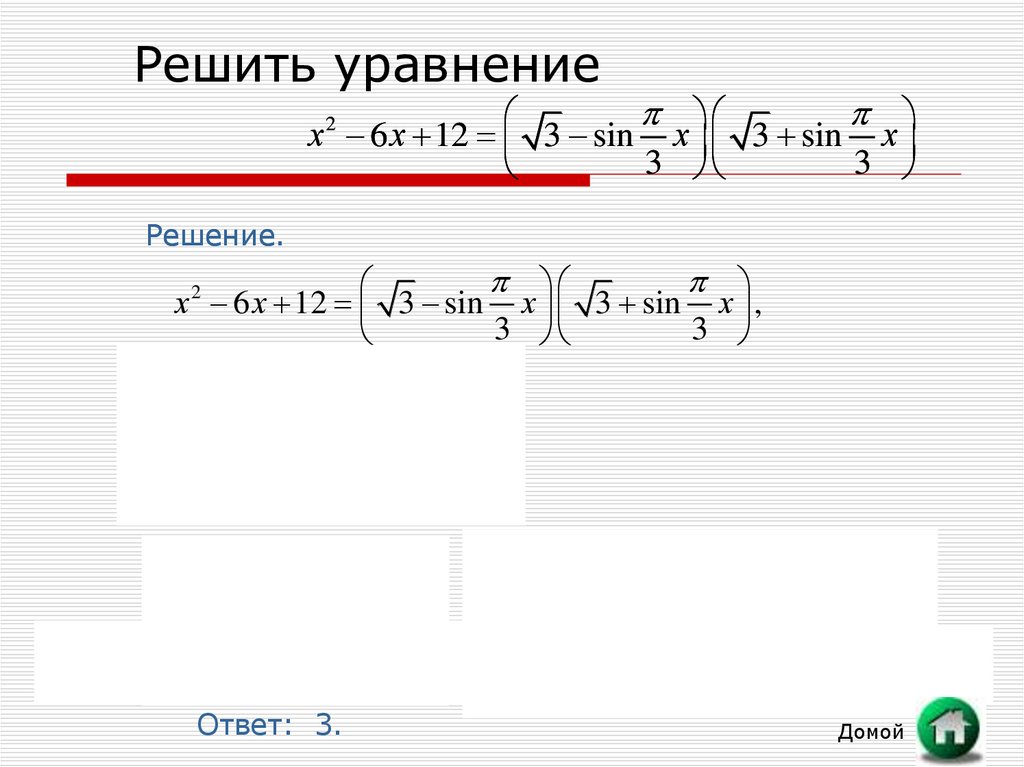
4. Решить уравнение

1
x
х 2 sin
х
2
Решение.
2 2 sin
x
2
2
Если х<0, то
1
х 2 , тогда
х
1
х х 2,
х 1.
2 sin x 2
2
1
х 2,
1
х
Если х>0, то х 2 , тогда
х
2 sin x 2
2
Ответ: -1; 1.
х 1.
Домой

5. Решить уравнение

х 2 х 2 cos
2
2
x 1 sin 5x
Решение.
х 2 2 х 2 cos 2 x 1 sin 5 x ,
х 2 2 х 2 cos x 1 sin 5 x .
f ( x) х 2 2 х 2;
g ( x) cos x 1 sin 5 x .
2
х0 1,
2
f ( x0 ) 1,
1 cos x 1 sin 5 x 1,
f ( x) 1
0 cos x 1 sin 5 x 1
0 g ( x) 1
Домой

6. Решить уравнение

х 2 х 2 cos
2
Решение.
2
x 1 sin 5x
х 2 2 х 2 cos 2 x 1 sin 5 x ,
2
f ( x) х 2 2 х 2; х 2 х 2 cos gx( x1
) sin
cos5 x x. 1 sin 5 x .
2
1,
2
f ( x0 ) 1,
х0
1 cos x 1 sin 5 x 1,
0 cos x 1 sin 5 x 1
f ( x) 1
х 2 2 х 2 1,
f ( x) g ( x)
cos x 1 sin 5 x 1.
cos 1 1 sin 5 x cos 0 1.
0 g ( x) 1
х 2 2 х 1 0, х 1.
Ответ: 1.
Домой

7. Решить уравнение

х 2 6 х 12 3 sin
3
x 3 sin
3
x
Решение.
х 6 х 12 3 sin
3
2
х 2 6 х 12 3 sin 2
х 6 х 9 sin
2
2
3
3
x 3 sin
3
x ,
x,
x,
х 3 2 0,
2
2
х
3
sin
x
2
3
x 0;
sin
3
Ответ: 3.
х 3.
Домой

8. Решить уравнение

log3 х 2 2 х 10 х 2 2 х 2 3
Решение.
log3 х 2 2 х 10 х 2 2 х 2 3
log3 х 2 2 х 10 3 х 2 2 х 2
f ( x) log3 х 2 2 х 10
t ( x) х 2 2 х 10,
f (t ) log 3 t , 3 1
t 9,
t 9.
t 0;
x0 1,
g ( x) 3 х 2 2 х 2
t (1) 9,
t ( x) 9.
f (t ) возрастающая.
f (t ) log 3 9,
f (t ) 2.
Домой

9.

y
у 2
у log3 t
2
1
0
t 9
1
t
9
Домой

10. Решить уравнение

log3 х 2 2 х 10 х 2 2 х 2 3
Решение.
log3 х 2 2 х 10 х 2 2 х 2 3
log3 х 2 2 х 10 3 х 2 2 х 2
f ( x) log3 х 2 2 х 10
f ( х) 2
g ( x) 3 х 2 2 х 2
Домой

11. Решить уравнение

log3 х 2 2 х 10 х 2 2 х 2 3
Решение.
log3 х 2 2 х 10 х 2 2 х 2 3
log3 х 2 2 х 10 3 х 2 2 х 2
f ( x) log3 х 2 2 х 10
f ( х) 3.
p( x) х 2 2 х 2,
p 1,
p 1,
р 0;
g ( x) 3 х 2 2 х 2
x0 1,
p(1) 1,
p( х) 1.
g ( p) 3 p ,
p 1,
p 1,
3 p 2.
g ( p) 2
Домой

12. Решить уравнение

log3 х 2 2 х 10 х 2 2 х 2 3
log3 х 2 2 х 10 3 х 2 2 х 2
f ( x) log3 х 2 2 х 10
g ( x) 3 х 2 2 х 2
g ( х) 2
f ( х) 2
log 3 х 2 2 х 10 2,
3 х 2 2 х 2 2.
Решение.
log 3 х 2 2 х 10 2,
х 2 2 х 10 9,
х2 2х 1 0
х 1
х 1
3 12 2 1 2 3 1 2.
Ответ: 1.
Домой

13. Множество значений сложной функции

Исследование функции элементарными
методами
Демонстрационный материал
Домой

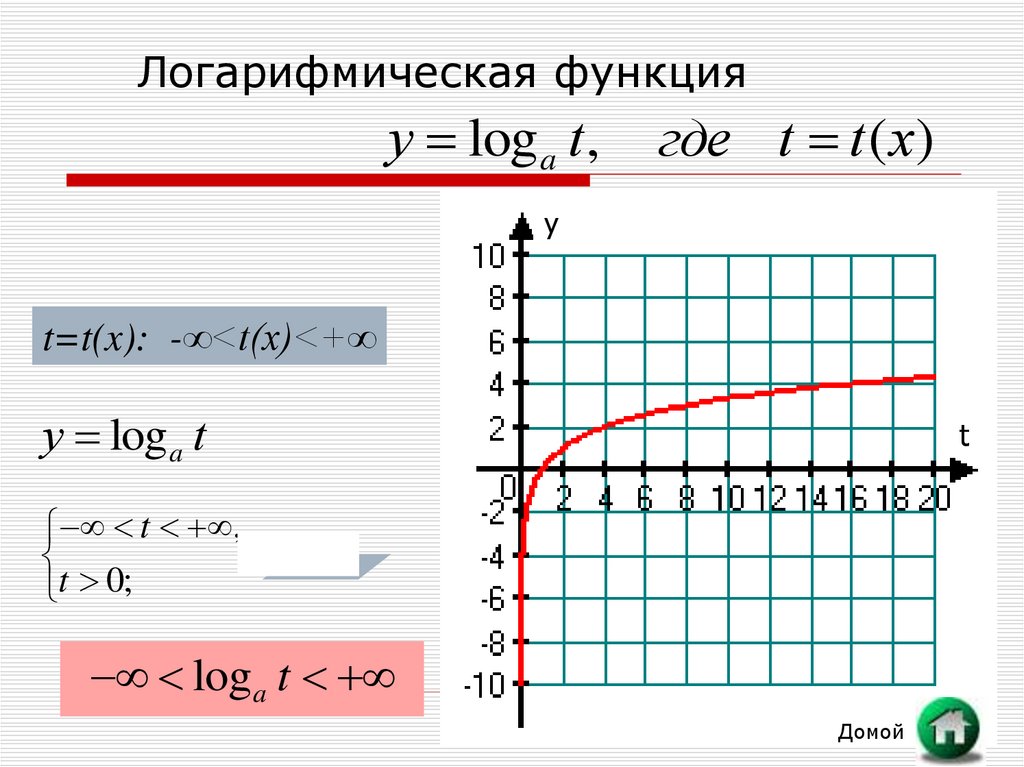
14. Логарифмическая функция

у log a t ,
где t t ( x)
0<а<1
y
t
t=t(x): -∞<t(x)<+∞
у log a t
t ,
t 0
t 0;
t
x
t=t(x)
log a t
Домой

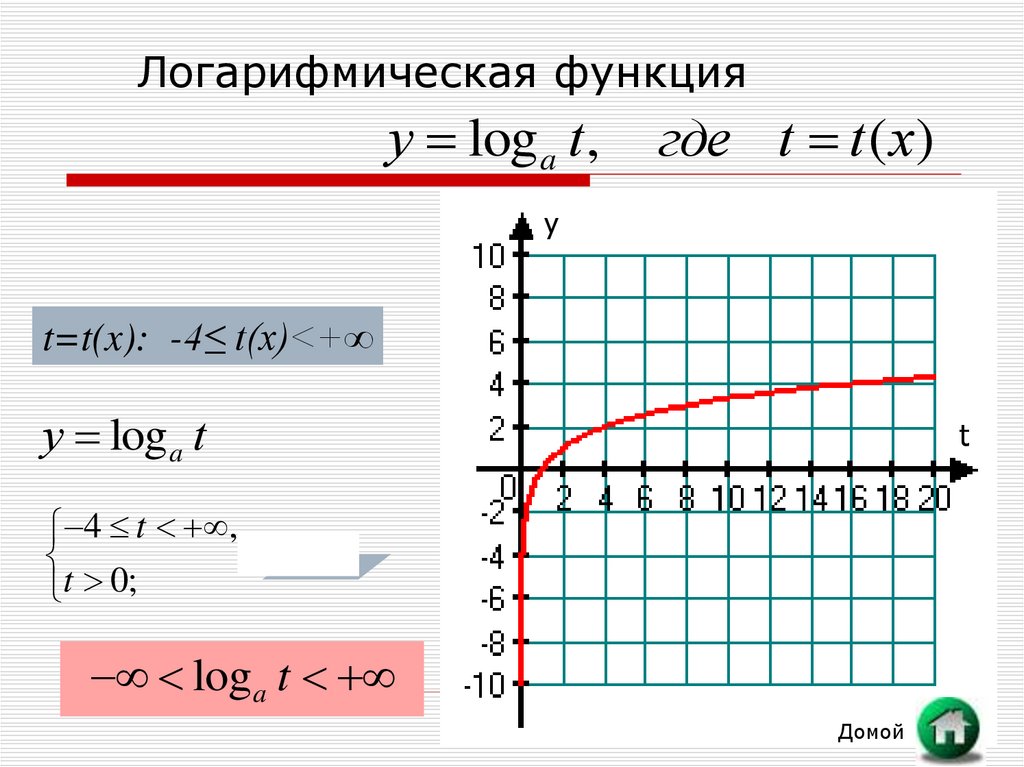
15. Логарифмическая функция

у log a t ,
где t t ( x)
y
t
t=t(x): -4≤ t(x)<+∞
t=t(x)
у log a t
t
x
4 t ,
t 0
t 0;
log a t
Домой

16. Логарифмическая функция

у log а t ,
где t t ( x)
t
y
t=t(x): - ∞ <t(x)≤ 4
a>1
t=t(x)
у log 2 t
у log а t
x t
t 4,
0 t 4
t 0;
log 2 t 2
Домой

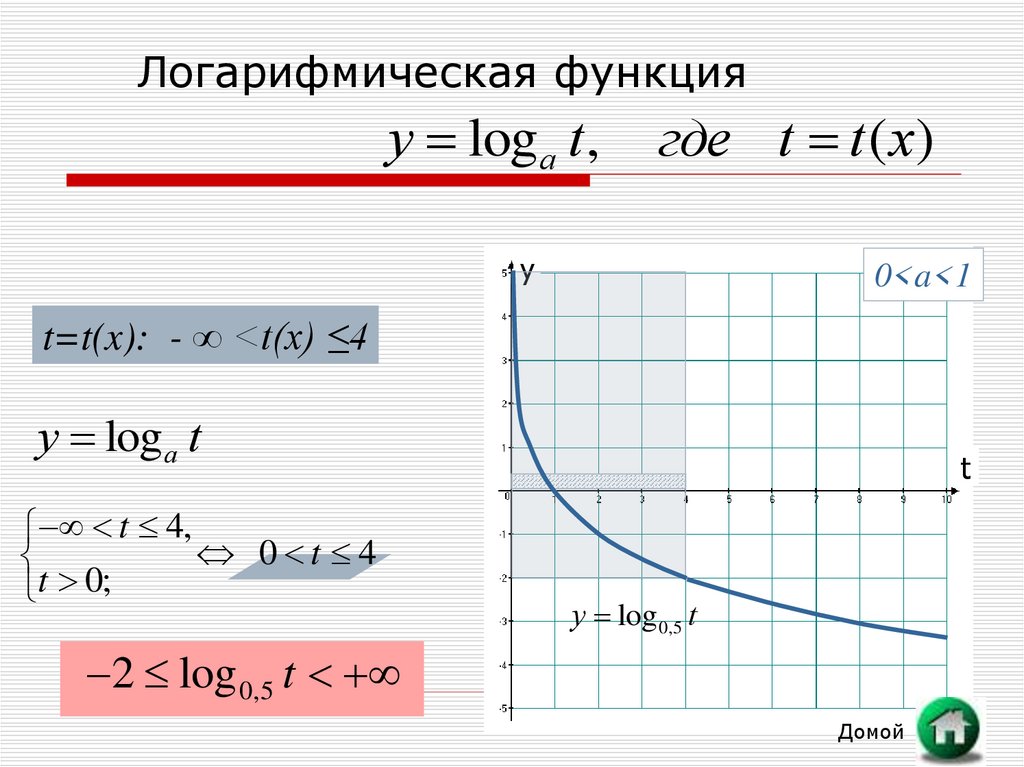
17. Логарифмическая функция

у log а t ,
где t t ( x)
y
0<a<1
t=t(x): - ∞ <t(x) ≤4
у log а t
t 4,
0 t 4
t 0;
t
у log 0,5 t
2 log 0,5 t
Домой

18. Вернуться к оглавлению

Домой