Similar presentations:
Уравнения математической физики
1.
•Уравнения математическойфизики
2.
1. Пример 1. Найти функцию z z x, y , удовлетворяющуюz
дифференциальному уравнению
1
x
Решение. Интегрируя, получим z x y , где y —
произвольная функция. Это—общее решение данного
дифференциального уравнения.
3.
4.
z1. Пример 2. Решить уравнение 2 6 y , где z z x, y .
y
2
Решение. Дважды интегрируя по y , получаем
z
2
3
3 y x , z y y x x , где x и x —
y
произвольные функции.
5.
6.
7.
1. Определить тип уравненияu
u u u
3 2 10
3 2 5u 0 .
x
x y y x
2
2
2
Решение.
2
Здесь a 3 , 2 b 10 , b 5 , c 3 , b ac 25 9 16 0 , следовательно, это —
уравнение гиперболического типа во всех точках плоскости.
8.
9.
10. Определить типы следующих ДУ в частных производных.
ПРИМЕР 1).2
2
2
u
u
u
u
2
2
0
2 y 2 3x
y
x
2
y
x y
y
x
главная часть
ПРИМЕР 2).
2
2
2
u
u
u
2
4 2 0
6cos x
2 3sin x
2
x y
y
x
главная часть
ПРИМЕР 3).
2u 2u
2 0
2
y
x
главная часть
11. РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЯ СТРУНЫ МЕТОДОМ ДАЛАМБЕРА
Свободные колебания u u( x, t ) бесконечной однороднойструны описываются уравнением в частных производных второго
порядка гиперболического типа
u
2
t
2
a
2
2
x
u
,
2
которое называется волновым уравнением.
(1)
12.
Для определения движения струны необходимо задать начальныеусловия: ее форму в начальный момент времени
u t 0 f ( x) ,
(2)
и начальную скорость точек
u
F ( x) .
t t 0
(3)
Решение уравнения (1) с начальными условиями (2)-(3) может
быть найдено методом Даламбера:
f ( x at) f ( x at) 1 x at
u( x, t )
F ( z )dz .
2
2a x at
(4)
13.
1. Пример 1. Используя формулу Даламбера, найти решенияследующих задач Коши
x ,0 t :
u x, t
2u 2u
a) Найти форму бесконечной струны, определяемую уравнением 2 2 в
t
x
u
момент времени
при начальных условиях u x,0 sin x ,
x,0 cos x .
t
2
Решение. Исходя из условий задачи x sin x , x cos x , найдем форму струны
в момент времени t :
sin x t sin x t 1 x t
1
x t
u x, t
cos d sin x cos t sin x t
2
2 x t
2
sin x cos t sin t cos x sin x t .
Полагая t , получаем u x, sin x cos x .
2
2
2
14.
Пример 2. Найти уравнение u u( x, t ) формы однородной2
2u
u
2
a
бесконечной струны, определенной уравнением
при
2
2
t
x
x
sin x u
начальных условиях u t 0
и
.
2
t t 0 1 x
x
Решение. Решение данной задачи, описывающее форму
однородной бесконечной струны, находим методом Даламбера по
x
sin x
формуле (6.4). Здесь f ( x )
; F ( x)
. Отсюда
2
x
1 x
1 sin( x at) sin( x at) 1 x at z
u ( x, t )
dz
2
2 x at
x at 2a x at 1 z
15.
1 ( x at )(sin x cos at cos x sin at ) ( x at )(sin x cos at cos x sin at )2
( x at )( x at )
1
ln(1 z 2 )
4a
x sin x cosat at cos x sin at
x a t
2
2 2
x at
x at
1 1 ( x at)
ln
.
2
4a 1 ( x at)
2
16.
Пример3.
Найти
начальных условиях u t 0
решение
уравнения
2u
t
2
a2
2u
x
2
при
u
x и
sin x .
t t 0
Решение. Искомое решение найдем из формулы (6.4) при
f ( x) x и F ( x) sin x . При этом получаем
x at x at 1 x at
1
x at
u ( x, t )
sin
zdz
x
cos
z
x at
2
2a x at
2a
cos(x at) cos(x at)
2a
cos x cosat sin x sin at cos x cosat sin x sin at
x
2a
sin x sin at
.
x
a
x
17.
a) Найти решение уравнения2u 2u
2 при начальных условиях
2
t x
sin x u
,
u x,0
x,0 0 .
x t
x sin x cos at at cos x sin at
Ответ: u x, t
.
2
2 2
x a t



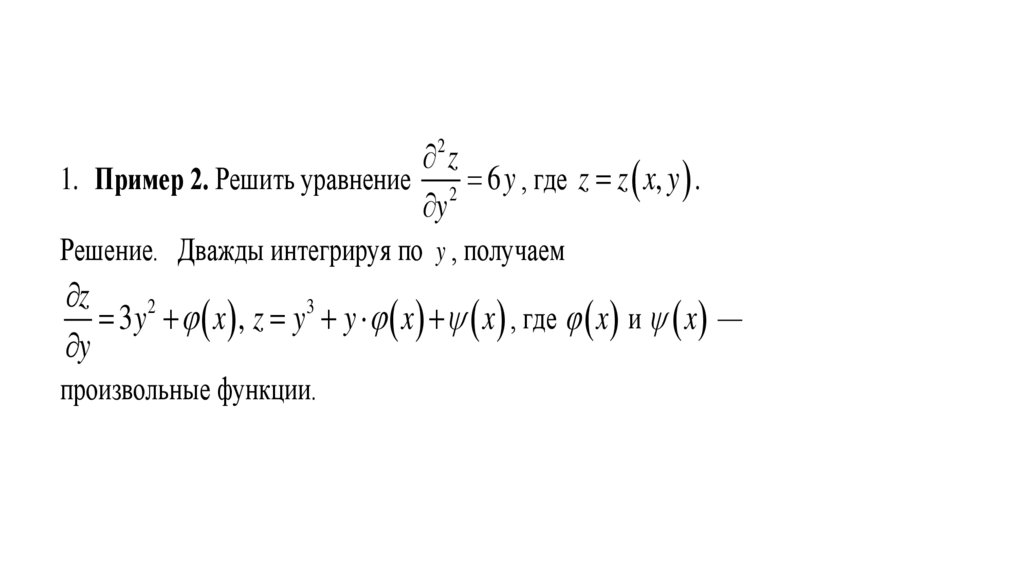













 mathematics
mathematics physics
physics








