Дробно-дифференциальная популяционная модель с нелокальной квадратичной нелинейностью

1.

Министерство науки и высшего образования Российской Федерации
ФГБОУ ВО «АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Факультет математики и информатики
Кафедра математического анализа и моделирования
Направление подготовки 01.03.02 – Прикладная математика и информатика
Направленность (профиль) образовательной программы– «Прикладная математика и информатика»
БАКАЛАВРСКАЯ РАБОТА
ДРОБНО-ДИФФЕРЕНЦИАЛЬНАЯ ПОПУЛЯЦИОННАЯ МОДЕЛЬ
С НЕЛОКАЛЬНОЙ КВАДРАТИЧНОЙ НЕЛИНЕЙНОСТЬЮ
Исполнитель: студент группы 952-ом Д.Е. Миньковский
Научный руководитель: канд. физ.-мат. наук Л.И. Мороз

2.

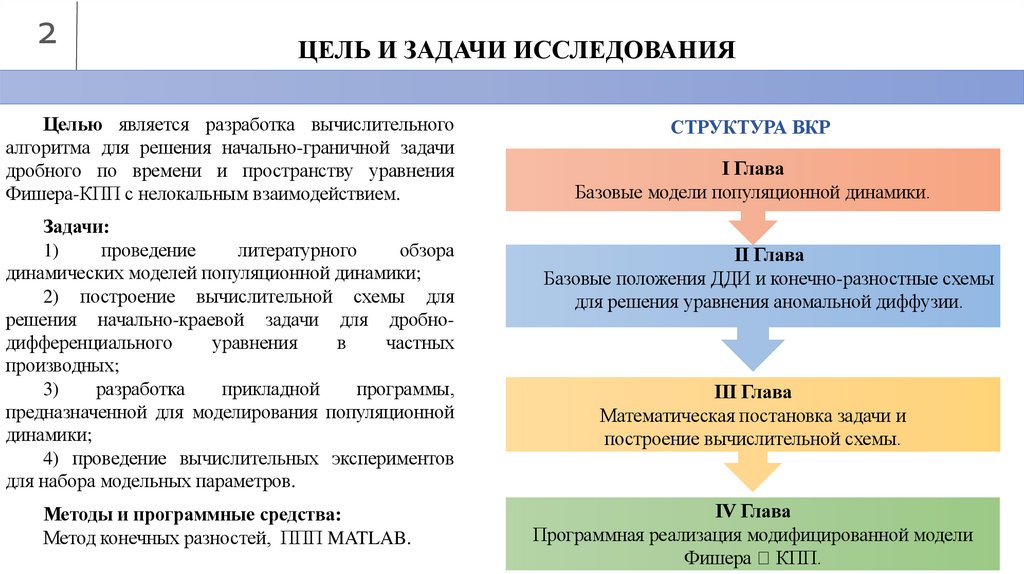
2
ЦЕЛЬ И ЗАДАЧИ ИССЛЕДОВАНИЯ
Целью является разработка вычислительного
алгоритма для решения начально-граничной задачи
дробного по времени и пространству уравнения
Фишера-КПП с нелокальным взаимодействием.
Задачи:
1)
проведение
литературного
обзора
динамических моделей популяционной динамики;
2) построение вычислительной схемы для
решения начально-краевой задачи для дробнодифференциального
уравнения
в
частных
производных;
3)
разработка
прикладной
программы,
предназначенной для моделирования популяционной
динамики;
4) проведение вычислительных экспериментов
для набора модельных параметров.
Методы и программные средства:
Метод конечных разностей, ППП MATLAB.
СТРУКТУРА ВКР
I Глава
Базовые модели популяционной динамики.
II Глава
Базовые положения ДДИ и конечно-разностные схемы
для решения уравнения аномальной диффузии.
III Глава
Математическая постановка задачи и
построение вычислительной схемы.
IV Глава
Программная реализация модифицированной модели
Фишера КПП.

3.

3
СТЕПЕНЬ ИЗУЧЕННОСТИ И НАУЧНОЙ РАЗРАБОТАННОСТИ ТЕМЫ
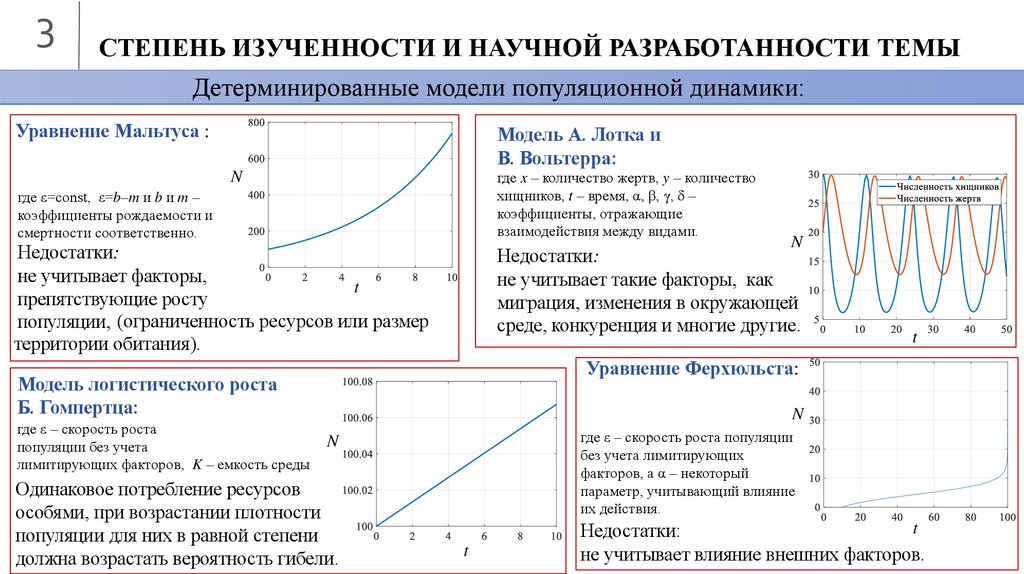
Детерминированные модели популяционной динамики:
Уравнение Мальтуса :
Модель А. Лотка и
В. Вольтерра:
где x – количество жертв, y – количество
хищников, t – время, α, β, γ, δ –
коэффициенты, отражающие
взаимодействия между видами.
N
где ε=const, ε=b–m и b и m –
коэффициенты рождаемости и
смертности соответственно.
территории обитания)
Недостатки:
не учитывает факторы,
t
препятствующие росту
популяции, (ограниченность ресурсов или размер
территории обитания).
t
Уравнение Ферхюльста:
Модель логистического роста
Б. Гомпертца:
где ε – скорость роста
популяции без учета
лимитирующих факторов, K – емкость среды
N
Недостатки:
не учитывает такие факторы, как
миграция, изменения в окружающей
среде, конкуренция и многие другие.
N
где ε – скорость роста популяции
без учета лимитирующих
факторов, а α – некоторый
параметр, учитывающий влияние
их действия.
N
Одинаковое потребление ресурсов
особями, при возрастании плотности
популяции для них в равной степени
должна возрастать вероятность гибели.
t
t
Недостатки:
не учитывает влияние внешних факторов.

4.

4 СТЕПЕНЬ ИЗУЧЕННОСТИ И НАУЧНОЙ РАЗРАБОТАННОСТИ ТЕМЫ
Уравнение Фишера – Колмогорова – Петровского – Пискунова
Базовая модель пространственного распределения популяции:
Приложения уравнения ФКПП:
задачи
теплои
массообмена,
теория горения, биология (популяционная
динамика), экология, физика плазмы,
D – коэффициент диффузии; a – темп роста популяции; b – коэффициент потерь. задачи теории фазовых переходов.
1937
…
1990
…
2003
…
2011
…
2015
…
Классическое
уравнение ФКПП
Уравнение ФКПП с
Уравнение ФКПП с
Уравнение ФКПП с
Уравнение ФКПП с
запаздыванием
дробной производной
адвекцией
Fisher R.A.;
Колмогоров А. Н. ,
Петровский И. Г.,
Пискунов Н. С.
Britton N. F.;
Gourley S. A.;
Wu J.; Ashwin P.
нелокальной
квадратичной
нелинейностью
Fuetnes M.A.;
Трифонов А.Ю.,
Шаповалов А.В.
Berestycki H.,
Alfaro M., Logak E.;
Roquejoffre J.-M., Rossi L.; Gu Н., Lou В., Zhou М.
Stan D., Vazquez L.;
Прозоров А.А.
Дробно-дифференциальные модели (бактерии):
[Kaur A., et al., J. of food science, 2008; S.Z. Rida et al., J Stat Phys, 2010; Kuttler A., Maslovskaya A., Appl. Math. Mod., 2021].
* приведен не полный
перечень (включены наиболее
значимые результаты в
рамках темы исследования)

5.

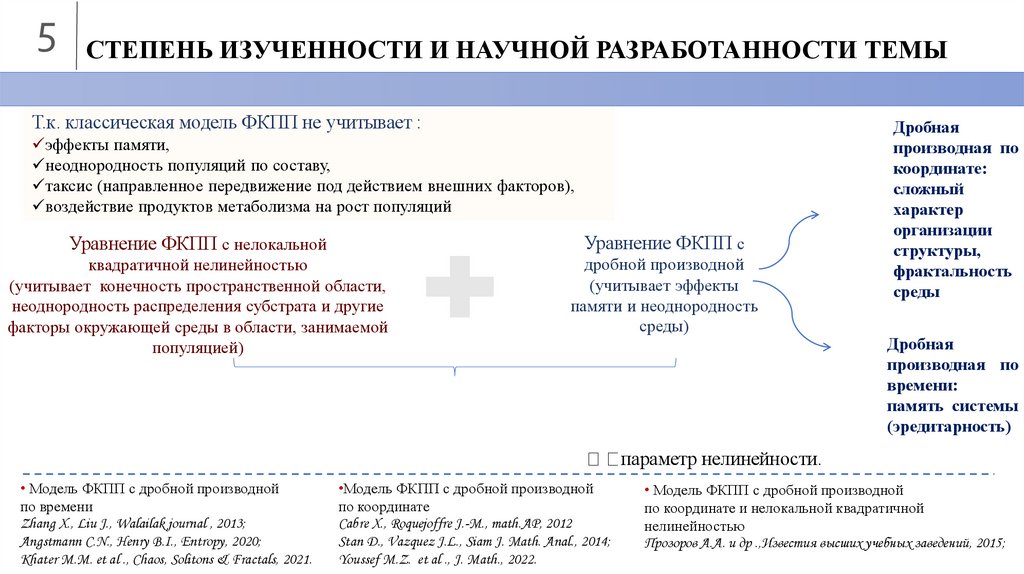
5 СТЕПЕНЬ ИЗУЧЕННОСТИ И НАУЧНОЙ РАЗРАБОТАННОСТИ ТЕМЫ
Т.к. классическая модель ФКПП не учитывает :
эффекты памяти,
неоднородность популяций по составу,
таксис (направленное передвижение под действием внешних факторов),
воздействие продуктов метаболизма на рост популяций
Уравнение ФКПП с нелокальной
Уравнение ФКПП с
квадратичной нелинейностью
(учитывает конечность пространственной области,
неоднородность распределения субстрата и другие
факторы окружающей среды в области, занимаемой
популяцией)
дробной производной
(учитывает эффекты
памяти и неоднородность
среды)
Дробная
производная по
координате:
сложный
характер
организации
структуры,
фрактальность
среды
Дробная
производная по
времени:
память системы
(эредитарность)
параметр нелинейности.
• Модель ФКПП с дробной производной
по времени
Zhang X., Liu J., Walailak journal , 2013;
Angstmann C.N., Henry B.I., Entropy, 2020;
Khater M.M. et al ., Chaos, Solitons & Fractals, 2021.
•Модель ФКПП с дробной производной
по координате
Cabre X., Roquejoffre J.-M., math.AP, 2012
Stan D., Vazquez J.L., Siam J. Math. Anal., 2014;
Youssef M.Z. et al ., J. Math., 2022.
• Модель ФКПП с дробной производной
по координате и нелокальной квадратичной
нелинейностью
Прозоров А.А. и др .,Известия высших учебных заведений, 2015;

6.

,
6
ДРОБНО-ДИФФЕРЕНЦИАЛЬНАЯ МОДЕЛЬ ФИШЕРА
КПП
Считаем пространство одномерным.
Область, в которой взаимодействуют особи
микробной популяции
узкая и длинная
трубка. Вдоль трубки осуществляются
процессы переноса, в ее поперечном
сечении происходит полное внутреннее
перемешивание.
Для начала рассмотрим модель ФКПП с дробными производными
Начальное условие:
Граничные условия:
Здесь 0<α<1, 1< β< 2 – порядки дробных производных Римана – Лиувилля по времени и пространству.
Производная
Римана – Лиувилля
!
где Г( ) – гамма-функция Эйлера.
Новизна: впервые рассмотрена модель ФКПП с дробной производной Римана
координате, так и по времени.
Лиувилля как по

7.

7
ПОСТРОЕНИЕ ВЫЧИСЛИТЕЛЬНОЙ СХЕМЫ
– пространственно-временная сетка.
Шаблон неявной схемы
• Аппроксимация дробной производной
[Meerschaert M.M., Tadjeran C.// J. Comp. Appl. Math, 2004]
нормированные веса Грюнвальда
Летникова.
К-Р аппроксимации производных Грюнвальда
Летникова
Аппроксимация нелинейной части
Итоговая схема имеет порядок аппроксимации O( t+ x)
Идейный смысл использования понятия дробной производной для
моделирования динамических систем: каждое последующее состояние
определяется через все предшествующие.
Решение уравнения аномальной диффузии (линейные задачи) методом конечных разностей:
[Meerschaert M.M., Tadjeran C., J. Comp. Appl. Math, 2004; Петухов А.А., Ревизников Д.Л., Вестник МАИ, 2009]
! Моделирование систем с
«полной памятью»:
достаточно ресурсоемкие
вычисления

8.

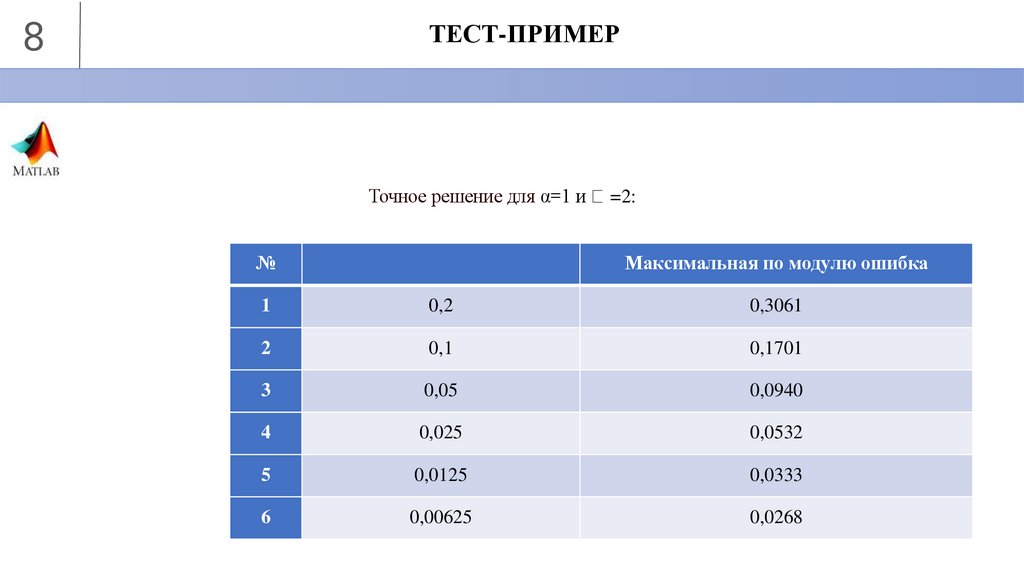
8
ТЕСТ-ПРИМЕР
Точное решение для α=1 и
№
=2:
Максимальная по модулю ошибка
1
0,2
0,3061
2
0,1
0,1701
3
0,05
0,0940
4
0,025
0,0532
5
0,0125
0,0333
6
0,00625
0,0268

9.

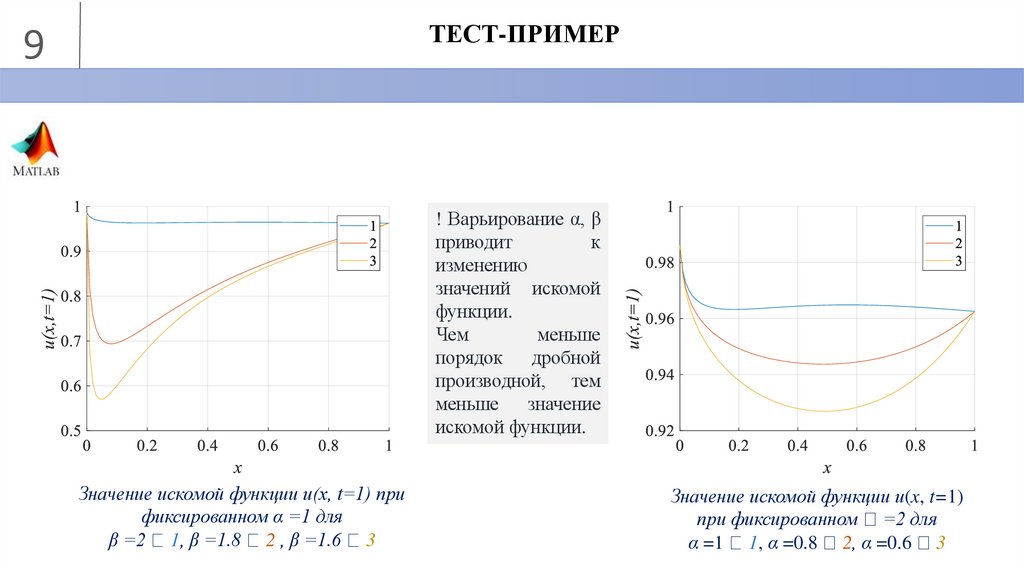
9
ТЕСТ-ПРИМЕР
! Варьирование α, β
приводит
к
изменению
значений искомой
функции.
Чем
меньше
порядок
дробной
производной, тем
меньше значение
искомой функции.
Значение искомой функции u(x, t=1) при
фиксированном α =1 для
β =2 1, β =1.8 2 , β =1.6 3
Значение искомой функции u(x, t=1)
при фиксированном =2 для
α =1 1, α =0.8 2, α =0.6 3

10.

10
ДРОБНО-ДИФФЕРЕНЦИАЛЬНАЯ МОДЕЛЬ ФИШЕРА
КПП С НЕЛОКАЛЬНОЙ КВАДРАТИЧНОЙ
НЕЛИНЕЙНОСТЬЮ
Далее рассмотрим модель ФКПП с дробными производными и с квадратичной нелинейностью
Начальное условие:
Граничные условия:
Здесь 0<α<1, 1< β< 2 – порядки дробных производных Римана – Лиувилля
по времени и пространству.
По формуле правых прямоугольников аппроксимируем интеграл
Таким образом, получим:
За
расчетное
время
tob
ненулевые значения u(x,t) не
должны достигать левой и правой
границ области x, –L<x<L.
Это
соответствует
нулевым
граничным
условиям
на
бесконечности
u(x,t)x→±∞=0.
В начальный момент времени в
ограниченную окрестность центра
области (подложки) с нанесенным
питательным веществом вносится
небольшое количество культуры.
Наблюдение ведется до контакта
области, занимаемой популяцией,
с границами подложки.

11.

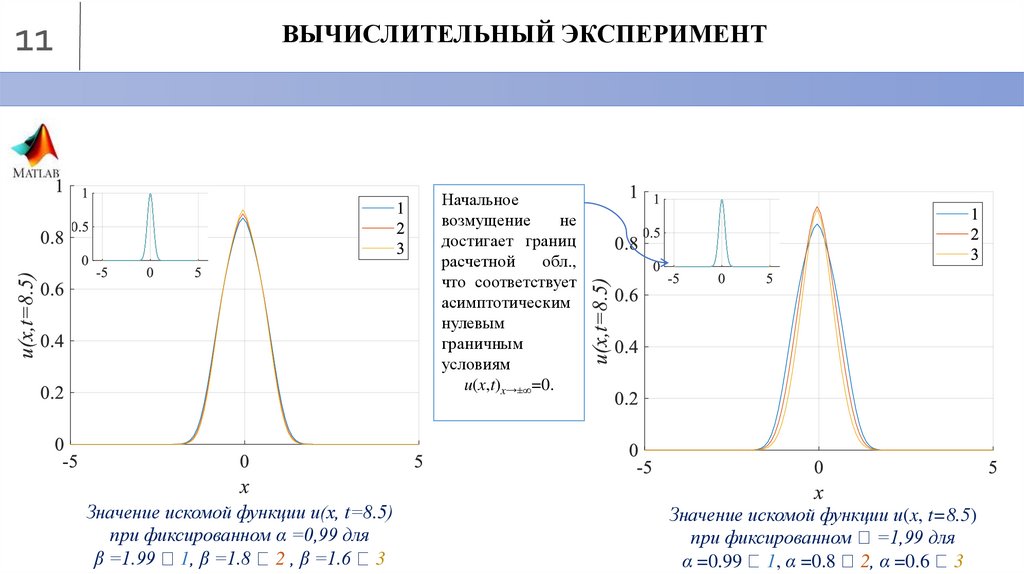
11
ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Начальное
возмущение
не
достигает границ
расчетной
обл.,
что соответствует
асимптотическим
нулевым
граничным
условиям
u(x,t)x→±∞=0.
Значение искомой функции u(x, t=8.5)
при фиксированном α =0,99 для
β =1.99 1, β =1.8 2 , β =1.6 3
Значение искомой функции u(x, t=8.5)
при фиксированном =1,99 для
α =0.99 1, α =0.8 2, α =0.6 3

12.

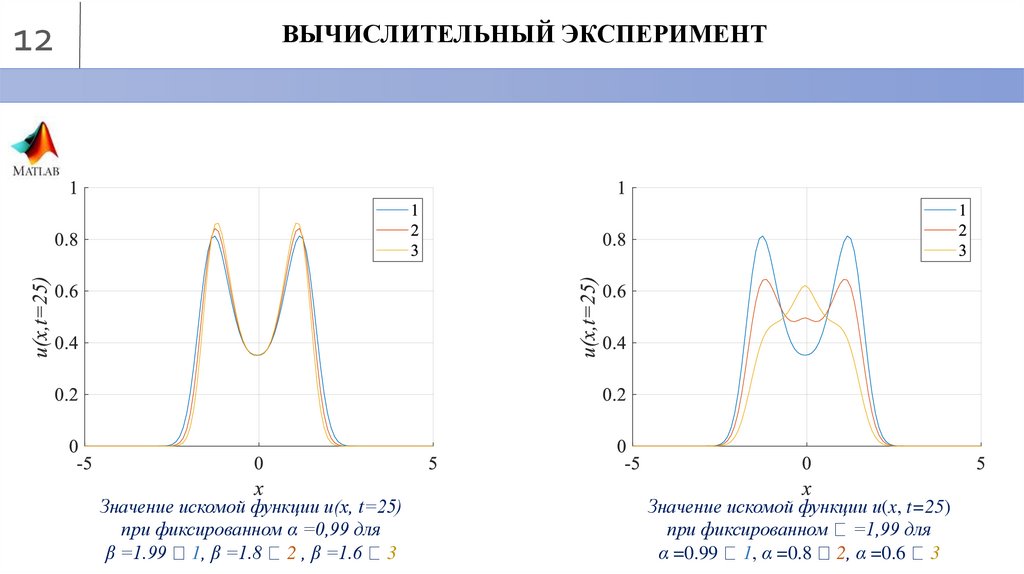
12
ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Значение искомой функции u(x, t=25)
при фиксированном α =0,99 для
β =1.99 1, β =1.8 2 , β =1.6 3
Значение искомой функции u(x, t=25)
при фиксированном =1,99 для
α =0.99 1, α =0.8 2, α =0.6 3

13.

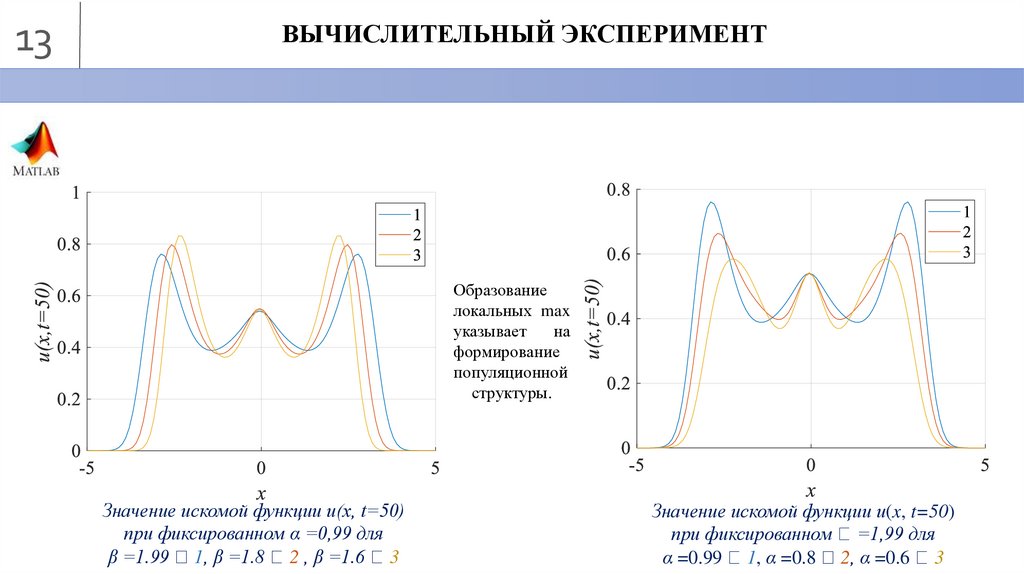
13
ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Образование
локальных max
указывает
на
формирование
популяционной
структуры.
Значение искомой функции u(x, t=50)
при фиксированном α =0,99 для
β =1.99 1, β =1.8 2 , β =1.6 3
Значение искомой функции u(x, t=50)
при фиксированном =1,99 для
α =0.99 1, α =0.8 2, α =0.6 3

14.

14
ЗАКЛЮЧЕНИЕ
В ходе выполнения бакалаврской работы:
– были рассмотрены модели популяционной динамики с использованием дробных
производных;
– построены вычислительные схемы для решения начально-краевых задач для
дробно-дифференциальных уравнений ФКПП без и с квадратичной нелинейностью;
– разработана прикладная программа, предназначенная для имитационного
моделирования популяционной динамики;
– проведена верификации полученных результатов на тест-примере с известным
аналитическим решением;
– проведены вычислительные эксперименты для набора модельных параметров.

15.

СПАСИБО ЗА
ВНИМАНИЕ

16.

Достоинства и недостатки определений дробных производных
I. Достоинства определений дробных производных
1. С дробной производной Римана – Лиувилля произвольная функция не обязательно должна быть непрерывной в нуле.
2. Дробная производная Капуто позволяет включить традиционные начальные и граничные условия в формулировку
задачи. Производная от константы равна нулю.
II. Недостатки определений дробных производных
1. Производная Римана – Лиувилля имеет определенные недостатки при попытке моделирования реальных явлений с
помощью уравнений с дробными производными. Производная Римана – Лиувилля от константы не равна нулю.
2. Производные Капуто определены только для дифференцируемых функций.

17.

Дробные производные
Свойства:
в общем случае не выполняется.

18.

УРАВНЕНИЕ АНОМАЛЬНОЙ ДИФФУЗИИ
При =1
1< β <2 – ускоренное блуждание;
β =1 – классический перенос;
β =2 – уравнение классической диффузии.
При β =2
0< <1 – субдиффузия или замедленное
блуждание;
=1 – классическая диффузия;
1< <2 – супердиффузия;
=2 – классическое волновое уравнение.