Детерминированные модели

1. Основы математической обработки информации

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
Основы математической
обработки информации
Семестр: 1
Лекции: 6
Практические занятия: 10
Контрольная работа: 1
Зачёт

2.

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
Лекция 4.
Детерминированные модели
§1. Пример модели, приводящей
дифференциальному уравнению
к
§2. Пример модели,
разностному уравнению
к
приводящей
Лекция 4. Детерминированные модели
2

3. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
Скорость остывания воды в чайнике
пропорциональна разности температуры чайника (Т)
и температуры кухни (20 С°). Чайник выключился в
10.20 при температуре воды 100С°.
В 10.30 температура воды в чайнике была 80 С°.
Выясните, когда температура воды в чайнике будет
равна 40 С°.
Лекция 4. Детерминированные модели
3

4. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
Исходные данные:
Температура кухни: 20 С°
Момент закипания чайника - 100С°: 0 мин
Момент остывания чайника до 80С°: 10 мин
Характер процесса остывания воды в
чайнике: скорость остывания воды в
чайнике
пропорциональна
разности
температуры чайника и температуры
кухни .
Содержательная постановка задачи
Разработать математическую модель, которая позволяет
определить температуру воды в чайнике в любой момент
времени.
Лекция 4. Детерминированные модели
4

5. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
1. t – время
(независимая переменная, аргумент) ;
T – температура воды в чайнике
(зависимая переменная, функция).
2. t – неотрицательно;
T (0)=100, Т(10)=80.
3. T’(t) =k(T-20).
Математическая постановка задачи
1. Выбрать переменные.
2. Записать ограничения на переменные.
3. Формулировка требований задачи на языке математики.
Лекция 4. Детерминированные модели
5

6. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
Математическая постановка задачи
Найти решение дифференциального уравнения
при следующих начальных условиях
T t k T 20
T 0 100, Т 10 80
Лекция 4. Детерминированные модели
6

7. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
T t k T 20
T 0 100, Т 10 80
Математическая постановка задачи
Задача свелась к обыкновенному дифференциальному
уравнению первого порядка с заданными начальными
условиями.
Существование и единственность решения такой задачи
доказывается в теории обыкновенных дифференциальных
уравнений (ОДУ), поэтому модель можно считать
корректной.
Лекция 4. Детерминированные модели
7

8. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
T t k T 20
T 0 100, Т 10 80
Аналитическое решение задачи
Данное ОДУ является уравнением с разделяющимися переменными.
Этапы решения такого уравнения известны:
1. Представить
производную
функции
в
виде
отношения
дифференциалов.
2. Разделить переменные.
3. Проинтегрировать обе части уравнения.
4. Выразить искомую функцию.
5. Найти значения констант по заданным начальным условиям.
6. Записать искомую функцию.
Лекция 4. Детерминированные модели
8

9. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
dT
k T 20
dt
dT
kdt
Т 20
T t k T 20
dT
Т 20 kdt
ln T 20 kt ln C
Аналитическое решение задачи
Данное ОДУ является уравнением с разделяющимися переменными.
Этапы решения такого уравнения известны:
1. Представить
производную
функции
в
виде
отношения
дифференциалов.
2. Разделить переменные.
3. Проинтегрировать обе части уравнения.
Лекция 4. Детерминированные модели
9

10. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
ln T 20 kt ln C
e ln T 20 e kt ln C
T 20 e kt e ln C
T 20 С e kt
T t 20 С e kt
Аналитическое решение задачи
Данное ОДУ является уравнением с разделяющимися переменными.
Этапы решения такого уравнения известны:
4. Выразить искомую функцию.
Лекция 4. Детерминированные модели
10

11. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
k 0
kt
20
С
e
100
,
T t 20 С e
k 10
T 0 100, Т 10 80
20
С
e
80
С 80,
С 80,
С
80
,
k 10
20 80 e 80 k 10 3
1 3
e
k ln
4
10 4
Аналитическое решение задачи
Данное ОДУ является уравнением с разделяющимися переменными.
Этапы решения такого уравнения известны:
5. Найти значения констант по заданным начальным условиям.
Лекция 4. Детерминированные модели
11

12. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
kt
T t 20 С e
T t 20 80e
1 3
ln t
10 4
С 80,
1 3
k 10 ln 4
Аналитическое решение задачи
Данное ОДУ является уравнением с разделяющимися переменными.
Этапы решения такого уравнения известны:
6. Записать искомую функцию.
Лекция 4. Детерминированные модели
12

13. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
T t 20 80e
1 3
ln t
10 4
Проверка адекватности модели
В любой момент времени температура воды в чайнике не
ниже температуры кухни.
В начальный момент времени температура воды в чайнике
100С°.
Через 10 минут температура воды в чайнике 80С°.
Лекция 4. Детерминированные модели
13

14. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
20 80e
1 3
ln t
10 4
40
1 3
ln t
10 4
1
e
4
1 3
1
ln t ln
10 4
4
T t 20 80e
1 3
ln t
10 4
1
ln
4
1
t 10
10 log 3 10 log 4 4
3
4 4
3
ln
4
Практическое использование модели
Выясним, когда температура воды в чайнике будет равна 40 С°.
Лекция 4. Детерминированные модели
14

15. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
t 10 log 4 4
3
t 10 log 4 4 48, 188416793
3
10.20 48 11.08
T t 20 80e
1 3
ln t
10 4
Практическое использование модели
Выясним, когда температура воды в чайнике будет равна 40 С°.
Лекция 4. Детерминированные модели
15

16. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
Ответ: Приблизительно в 11.08
температура воды в чайнике будет
равна 40 С° .
Скорость остывания воды в чайнике
пропорциональна разности температуры чайника (Т)
и температуры кухни (20 С°). Чайник выключился в
10.20 при температуре воды 100С°.
В 10.30 температура воды в чайнике была 80 С°.
Выясните, когда температура воды в чайнике будет
равна 40 С°.
Лекция 4. Детерминированные модели
16

17. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
Пример корректного вопроса:
когда температура воды в чайнике
будет отличаться от температуры
кухни меньше, чем на 10 градусов?
Примеры некорректных вопросов:
когда температура воды в чайнике
будет 15 градусов?
какой была температура воды в
чайнике в 10.00?
Сформулируйте: а) корректный вопрос;
б) некорректный вопрос,
который можно изучать с помощью данной модели.
Лекция 4. Детерминированные модели
17

18. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
Пример корректного вопроса:
когда температура воды в чайнике
будет отличаться от температуры
кухни меньше, чем на 10 градусов?
T t 20 10
T t 20 80e
20 80e
1 3
ln t
10 4
1 3
ln t
10 4
1 3
ln t
10 4
20 10
1
10 ln
8 72,28262
t
3
ln
4
e
1
8
1 3
1
ln t ln
10 4
8
Ответ: через 72 минуты.
Лекция 4. Детерминированные модели
18

19. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
Пример некорректного вопроса:
когда температура воды в чайнике
будет 15 градусов?
T t 15
T t 20 80e
1 3
ln t
10 4
20 80e
1 3
ln t
10 4
15
e
1 3
ln t
10 4
5
80
t
Лекция 4. Детерминированные модели
19

20. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
Пример некорректного вопроса:
какой была температура воды в
чайнике в 10.00?
T 20 ?
T t 20 80e
1 3
ln t
10 4
T 20 20 80e
1 3
ln 20
10 4
20 80e
3
2 ln
4
20 80e
16
ln
9
16
20 80 162 100
9
Лекция 4. Детерминированные модели
20

21. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Лекция 4. Детерминированные модели
21

22. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
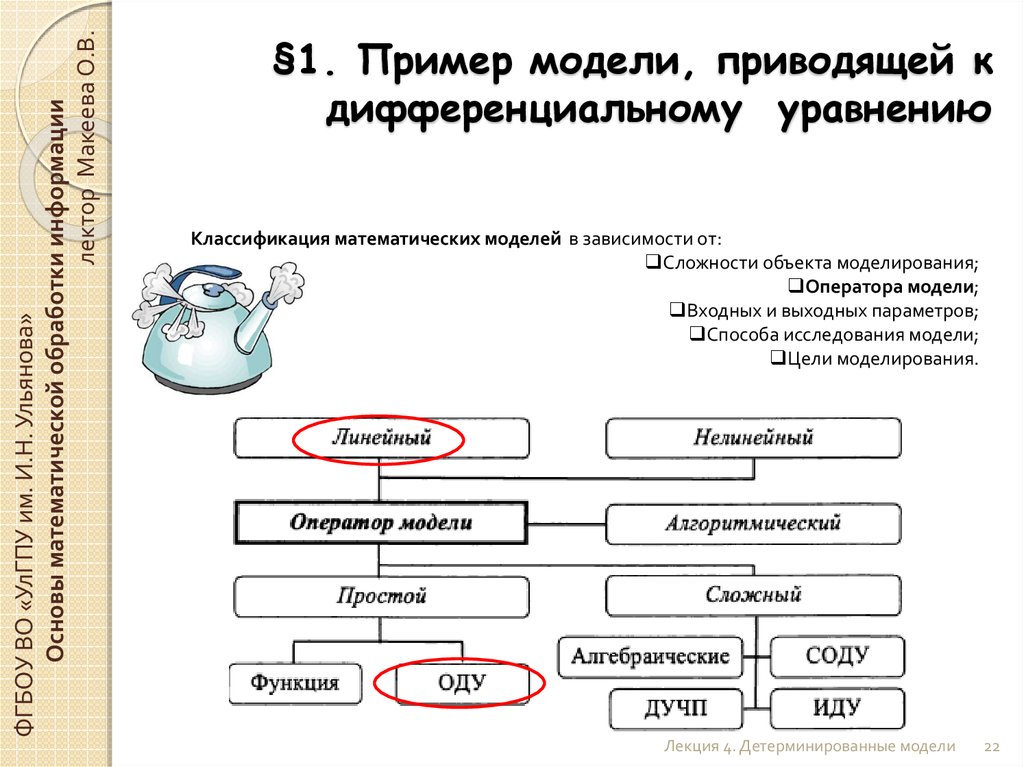
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Лекция 4. Детерминированные модели
22

23. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
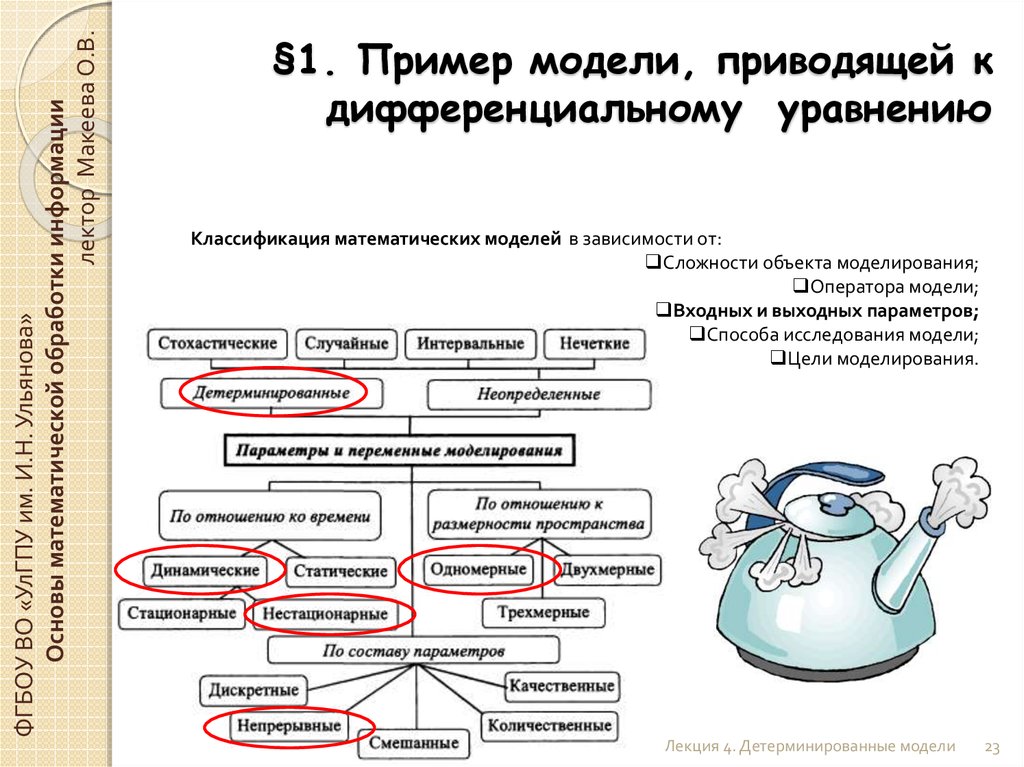
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Лекция 4. Детерминированные модели
23

24. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
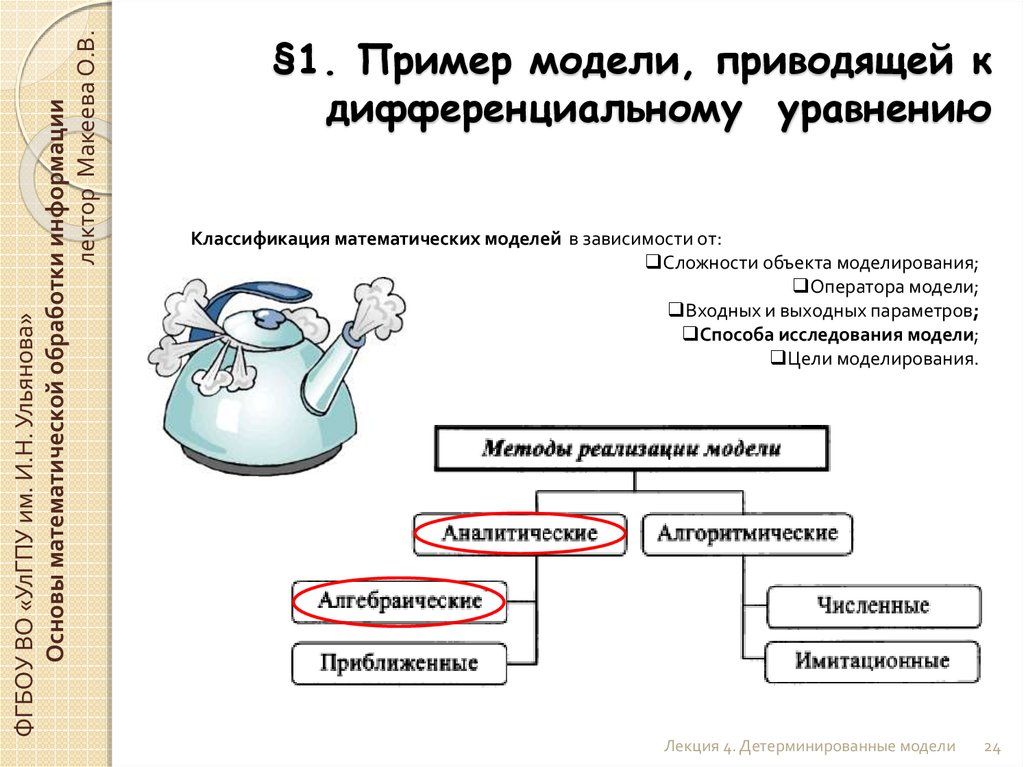
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Лекция 4. Детерминированные модели
24

25. §1. Пример модели, приводящей к дифференциальному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§1. Пример модели, приводящей к
дифференциальному уравнению
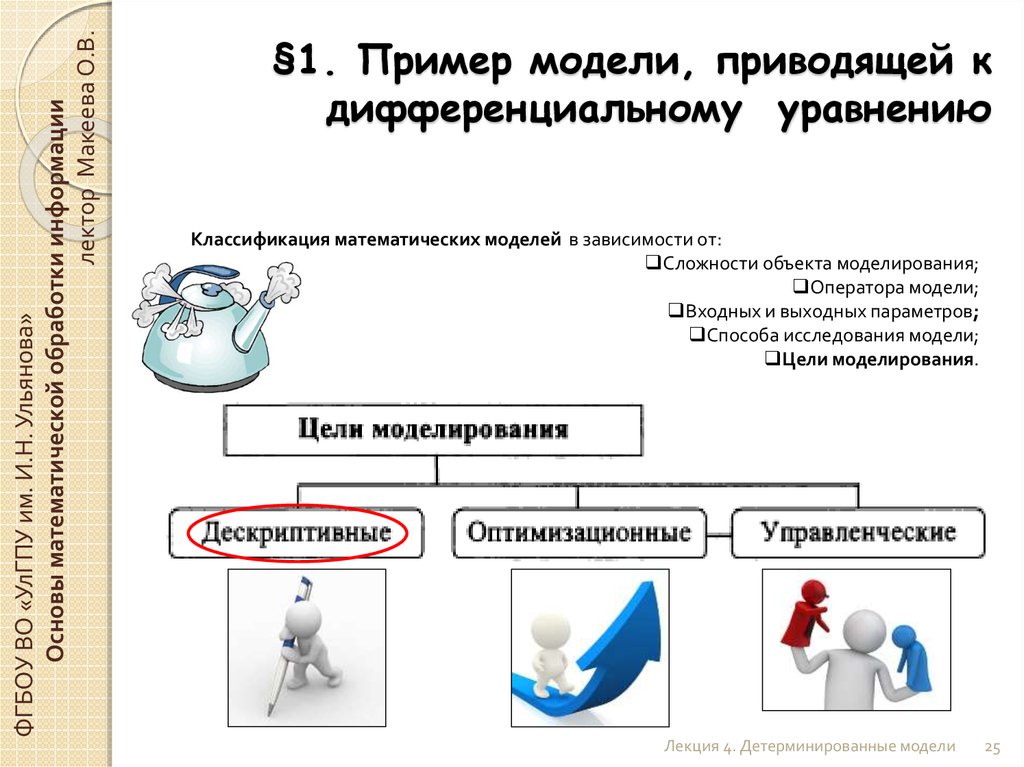
Классификация математических моделей в зависимости от:
Сложности объекта моделирования;
Оператора модели;
Входных и выходных параметров;
Способа исследования модели;
Цели моделирования.
Лекция 4. Детерминированные модели
25

26. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Лекция 4. Детерминированные модели
26

27. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Лекция 4. Детерминированные модели
27

28. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Лекция 4. Детерминированные модели
28

29. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Лекция 4. Детерминированные модели
29

30. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Лекция 4. Детерминированные модели
30

31. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Исходные данные:
Количество рыб
эксперимента: 0 .
в
озере
в
начале
Количество рыб, которое каждый год
выпускает в озеро зоолог: 100 .
Количество рыб,
погибают: 0.
которые
ежегодно
Характер процесса размножения рыб в
озере: популяция развивается с темпом
50% ежегодно .
Содержательная постановка задачи
Разработать математическую модель, которая позволяет
ежегодно определять численность популяции рыб в озере.
Лекция 4. Детерминированные модели
31

32. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
1. n – номер года
(независимая
аргумент) ;
переменная,
xn – численность популяции рыб в
n-ом году
(зависимая переменная, функция).
2. n – неотрицательно; x0=0
3. xn 1 1,5 xn 100
Математическая постановка задачи
1. Выбрать переменные.
2. Записать ограничения на переменные.
3. Формулировка требований задачи на языке математики.
Лекция 4. Детерминированные модели
32

33. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Математическая постановка задачи
Найти решение разностного уравнения
при следующем начальном условии
xn 1 1,5 xn 100
x0 0
Лекция 4. Детерминированные модели
33

34. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
xn 1 1,5 xn 100
x0 0
Математическая постановка задачи
Задача свелась разностному уравнению первого порядка с
заданным начальным условием.
Существование и единственность решения такой задачи
доказывается в теории разностных уравнений (РУ), поэтому
модель можно считать корректной.
Лекция 4. Детерминированные модели
34

35. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
xn 1 1,5 xn 100
x0 0
Аналитическое решение задачи
Данное РУ является линейным уравнением с постоянными
коэффициентами. Этапы решения такого уравнения известны:
1. Записать последовательно значения x1, x2, x3,…
2. По индукции получить зависимость xn=xn(n, x0).
Лекция 4. Детерминированные модели
35

36. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
xn 1 1,5 xn 100
x1 1,5x0 100
х2 1,5 x1 100 1,5 1,5 x0 100 100
1,5 x0 1,5 1 100
2
х3 1,5 x2 100 1,5 1,52 x0 1,5 1 100 100
1,53 x0 1,52 1,5 1 100
Аналитическое решение задачи
Данное РУ является линейным уравнением с постоянными
коэффициентами. Этапы решения такого уравнения известны:
1. Записать последовательно значения x1, x2, x3,…
Лекция 4. Детерминированные модели
36

37. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
х3 1,53 x0 1,52 1,5 1 100
хn 1,5n x0 1,5n 1 1,5n 2 ... 1,5 1 100
хn 1,5n x0 1 1,5 ... 1,5n 2 1,5n 1 100
bn q b1
Sn
,q 1
q 1
n 1
1
,
5
1,5 1
n
хn 1,5 x0
100 1,5n x0 200 1,5n 1
1,5 1
Аналитическое решение задачи
Данное РУ является линейным уравнением с постоянными
коэффициентами. Этапы решения такого уравнения известны:
2.
По индукции получить зависимость xn=xn(n, x0).
Лекция 4. Детерминированные модели
37

38. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
хn 1,5 x0 200 1,5 1
n
n
x0 0
Аналитическое решение задачи
Данное РУ является линейным уравнением с постоянными
коэффициентами. Этапы решения такого уравнения известны:
2.
По индукции получить зависимость xn=xn(n, x0).
Лекция 4. Детерминированные модели
38

39. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
хn 1,5 x0 200 1,5 1
n
n
x0 0
Проверка адекватности модели
В любой год численность популяции неотрицательна.
В год начала эксперимента численность популяции равна
нулю.
Лекция 4. Детерминированные модели
39

40. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
200 1,5 1 2000
1,5n 0 200 1,5n 1 2000
n
1,5n 1 10
1,5n 11
хn 1,5 x0 200 1,5 1
x0 0
n
n
n log 3 11
2
n 5,91393
Практическое использование модели
Выясним, через сколько лет численность популяции достигнет
2000 рыб.
Лекция 4. Детерминированные модели
40

41. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
n 6
хn 1,5n x0 200 1,5n 1
x0 0
Практическое использование модели
Выясним, через сколько лет численность популяции достигнет
2000 рыб.
Лекция 4. Детерминированные модели
41

42. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Ответ: Численность популяции достигнет 2000 рыб
через 6 лет после начала эксперимента.
Лекция 4. Детерминированные модели
42

43. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Пример 1:
какой будет численность
популяции через 3 года, если на
начало эксперимента в озере
обитало 10 рыб?
Приведите примеры задачи, которую можно решить с
помощью аналогичной модели и требуется изменить
лишь начальное условие.
Лекция 4. Детерминированные модели
43

44. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Пример 1:
какой будет численность
популяции через 3 года, если на
начало эксперимента в озере
обитало 10 рыб?
хn 1,5n x0 200 1,5n 1
x0 10
х3 1,53 10 200 1,53 1 508,75
Ответ: Численность популяции через три года составит
508 рыб.
Лекция 4. Детерминированные модели
44

45. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Пример 2:
сможет ли численность популяции
достичь 2000 особей, если рыбы
погибают с темпом 5% в год из-за
плохой экологической ситуации?
Приведите примеры задачи, которую можно решить с
помощью аналогичной модели, но потребуется
внести изменение в характер процесса развития
популяции.
Лекция 4. Детерминированные модели
45

46. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Пример 2:
сможет ли численность популяции
достичь 2000 особей, если рыбы
погибают с темпом 5% в год из-за
плохой экологической ситуации?
хn 1 0,95 xn 100
x0 0
хn 0,95n x0 1 0,95 ... 0,95n 2 0,95n 1 100
n 1
0
,
95
0,95 1
n
хn 0,95 x0
100
0,95 1
0,95n x0 2000 0,95n 1
Лекция 4. Детерминированные модели
46

47. §2. Пример модели, приводящей к разностному уравнению

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
§2. Пример модели, приводящей к
разностному уравнению
Пример 2:
сможет ли численность популяции
достичь 2000 особей, если рыбы
погибают с темпом 5% в год из-за
плохой экологической ситуации?
хn 0,95n x0 2000 0,95n 1
x0 0
1 2000
0,95n x0 2000 0,95n 1 2000
2000 0,95n
0,95 0
n
Ответ: Численность популяции никогда
не достигнет 2000 рыб.
Лекция 4. Детерминированные модели
47

48. Продолжение следует…

ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»
Основы математической обработки информации
лектор Макеева О.В.
Основы математической
обработки информации
Продолжение следует…