Математическое и имитационное моделирование. Имитационная модель

1. Математическое и имитационное моделирование

2. Имитационное моделирование

- численный метод проведения на
компьютерах вычислительных
экспериментов с математическими
моделями, имитирующими поведение
реальных объектов, процессов и
систем во времени в течение заданного
периода.

3. Имитационная модель

- это компьютерная программа,
позволяющая воспроизводить на ЭВМ
поведение отдельных элементов системы
и связей между ними в течение заданного
времени моделирования.
Имитационные (вычислительные)
эксперименты - это эксперименты с
ИМ.

4. Условия применения ИМ:

Если реальные эксперименты дороги,
невозможны и опасны
Когда необходимо наблюдение за
поведением элементов системы и контроль
за протеканием процессов путем их
замедления или ускорения
Когда особое значение имеет
последовательность процессов в
проектируемых системах для предсказания
узких мест их функционирования.
При подготовке специалистов как тренажеры

5. Цели имитационного мод-я.

Основная цель – анализ динамических
процессов с неподдающимися
аналитическому изучению сложными
связями между переменными.
Моделирующий алгоритм позволяет по
исходным данным, содержащим сведения о
начальном состоянии процесса (входной
информации) и его параметрах, получить
сведения о состояниях процесса на каждом
последующем шаге.

6. Достоинства ИМ

Часто это единственно возможный способ
получить хорошее решение
Возможность исследования систем на
разных уровнях детализации
Возможность исследования динамики
взаимодействия элементов системы во
времени
Возможность оценивания характеристики
системы в определенные моменты
времени.

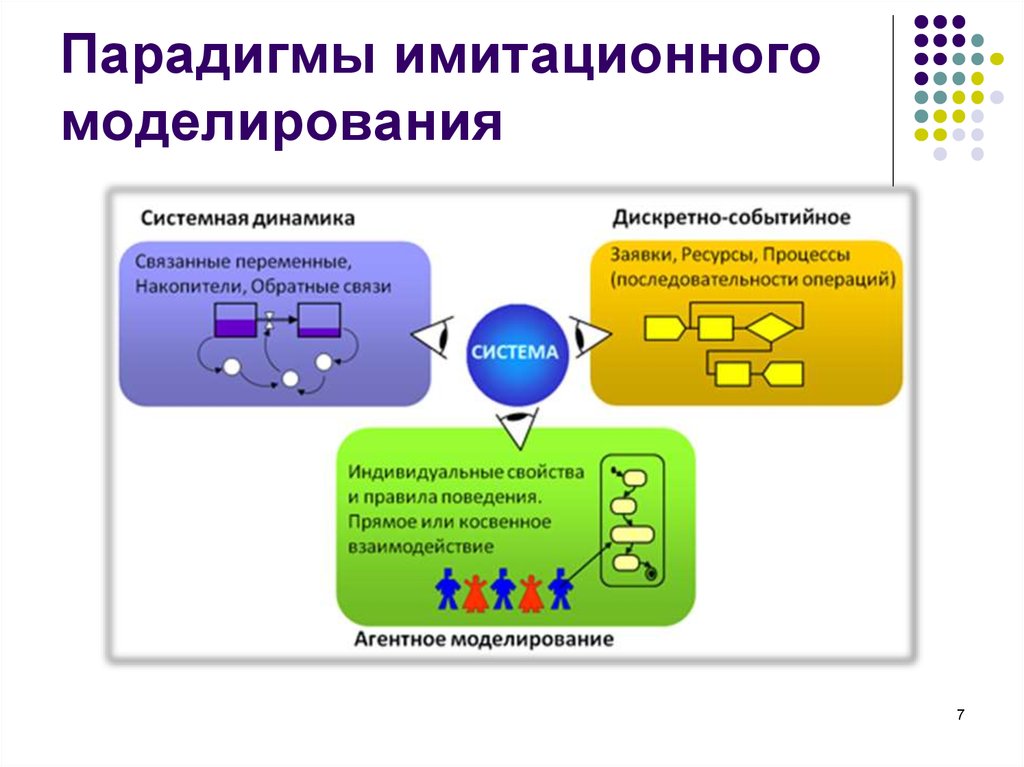
7. Парадигмы имитационного моделирования

7

8. Классические парадигмы

Дискретно-событийная или Процессная:
Последовательность отдельных важных
событий;
Последовательность операций над некими
объектами.
Системная динамика
Структура и динамика сложных систем;
Высокий уровень абстракции.
8

9. Агентное моделирование

Исследует:
Поведение децентрализованных агентов;
Влияние поведения агентов на поведение
системы в целом.
Определяется:
НЕ глобальными законами и правилами;
НО результатом индивидуальной
активности отдельных активных объектов.
9

10. Агентное моделирование

Основные особенности:
Наличие активных объектов – агентов;
Взаимодействие между агентами.
Применимость:
Задачи коммуникативного характера
(контакты между активными объектами);
Моделирование технологических
процессов.
10

11.

Модели
систем
Дискретная
Непрерывная
Зависимая
переменная
Зависимая
переменная
Время
Моменты
событий
Время
2

12. Дискретно-событийное моделирование

Дискретно-событийное моделирование —
подход к моделированию, предлагающий
абстрагироваться от непрерывной
природы событий и рассматривать только
основные события моделируемой
системы, такие как: «ожидание»,
«обработка заказа», «движение с грузом»,
«разгрузка» и другие.

13. Дискретно-событийное моделирование

Это моделирование систем, поведение
которых изменяется лишь в заданные
моменты времени.
Пример. Системы массового
обслуживания:
1) Средняя длина очереди;
2) Среднее время ожидания;
3) Количество обслуженных заявок.

14. Основные методы имита-ционного моделирования

Основные методы имитационного моделирования
1.
2.
3.
Аналитический метод
Метод статистического
моделирования
Комбинированный (аналитикостатистический) метод.

15. Метод статистического моделирования

- это численный метод решения задач
при помощи моделирования случайных
величин.

16. МЕТОДИКА метода статистического моделирования

1.
2.
3.
Метод Монте-Карло.
Вычисление реакции объекта,
процесса или системы на случайные
воздействия.
Статистическая обработка результатов
имитационного эксперимента.

17. Метод статистических испытаний. Метод Монте-Карло.

-
это численный метод, моделирующий
на ЭВМ псевдослучайные числовые
последовательности с заданными
вероятностными характеристиками.

18. Сущность метода Монте-Карло.

19. Непрерывное имитационное моделирование представляется с помощью непрерывно изменяющихся зависимых переменных во времени

Первое
уравнение определяет скорость
изменения s как функцию от s и t , второе
уравнение - начальное условие для переменной
состояния.
3

20. Модели Роста

(1)
(2)
4

21.

Систему обыкновенных
дифференциальных уравнений,
полученную в результате исследования
какого-либо явления или процесса,
называют непрерывной моделью этого
явления или процесса, поскольку все
переменные этой модели являются
непрерывными функциями времени.

22. Модели Роста

4

23. Модели Роста

24. Модели Роста

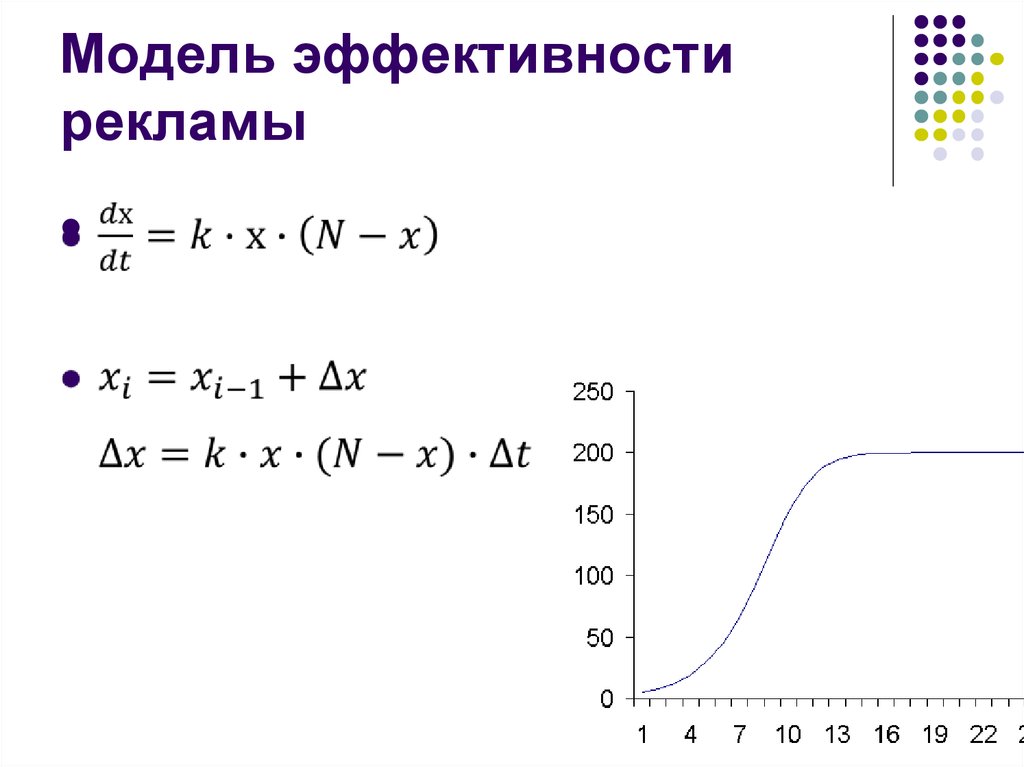
25. Конечно-разностные уравнения

26. Модель эффективности рекламы

27. Моделирование финансовой пирамиды

Банковская система любой страны как на
трех китах покоится на трех числах:
N1 > N2 > N3.
N1 - плата за кредит.
N2 - процент по вкладу.
N3 - это величина инфляции.
Разница между первым и вторым числом
(N1 > N2) заставляет банки прибыльно
работать.

28. Цель работы: Исследование зарождения, эволюции и гибели финансовой пирамиды

29. Примеры применения имитационных моделей

модели роста численности популяции.
Простейшая модель такого рода (закон
экспоненциального роста) была
использована в XIX веке Т. Мальтусом.
Недостаток: модель не учитывала, что
общий объем жизненных ресурсов
накладывает естественные ограничения на
динамику развития процесса.

30. Модель Мальтуса

Конечно-разностное уравнение динамики
численности населения:
Ni+1=Ni + rNi – mNi
или
Ni+1=Ni + (r – m)Ni
где разность (r – m) – коэффициент
прироста.
Если этот коэффициент больше нуля
(рождаемость выше смертности), население
растет, если меньше нуля – убывает.

31.

32. Модель Мальтуса

Описывает неограниченный,
экспоненциальный рост человечества.
В результате был получен весьма
неблагоприятный прогноз, связанный с
невозможностью обеспечить жизненными
ресурсами неограниченно растущее
население.

33. Модель роста народонаселения

Однако, экспоненциальный рост не может
продолжаться долго. Естественные
ограничения на него накладывает
внешняя среда, ресурсы которой не
безграничны.
В простейшем случае можно
предположить, что коэффициент прироста
не является постоянным, а убывает с
течением времени, по мере роста
населения.

34. Логистическая модель роста народонаселения

Логистическая модель роста
народонаселения была предложена
П. Ферхюльстом
(в этой модели предполагается, что
прирост численности в каждый момент
прямо пропорционален достигнутой
численности и обратно пропорционален
ее квадрату).

35. Модель Ферхюльста

Конечно-разностное уравнение динамики
численности населения:
Ni+1 = Ni +rNi – mNi – bNi2
Решение этого уравнения приводит к тому,
что численность населения не растет
неограниченно, а стремится к некоторой
предельной величине.

36.

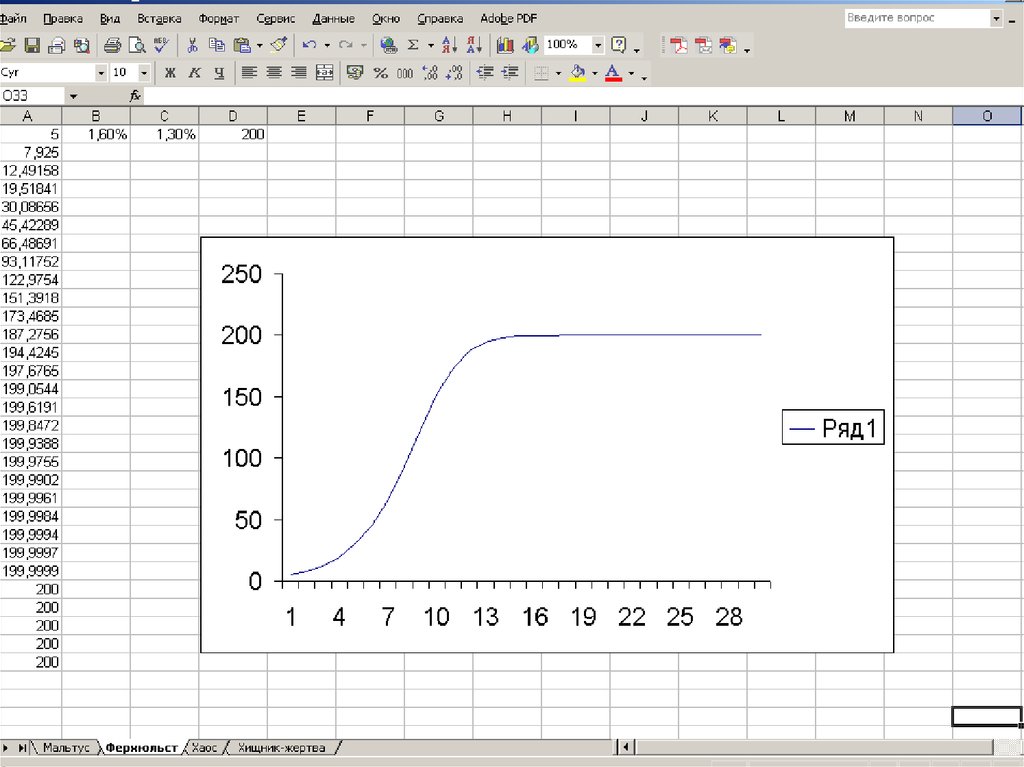
37. Модель Ферхюльста

График этого уравнения называется
логистической кривой.
Таким образом, система в данном случае
имеет устойчивое (стационарное) состояние;
этому состоянию соответствует прирост
населения, равный нулю (рождаемость
уравновешивается смертностью).

38. Модель «Хищник-Жертва»

Если динамических переменных больше
одной, тогда и уравнений
(дифференциальных или разностных)
должно быть несколько, т.е. это система
уравнений.
Пример: модель Лотки-Вольтерра (в
биологии известна как модель "хищникжертва", в политологии – как модель "народправительство", в истории – как модель
"бароны и крестьяне", в экономике как
модель конкуренции фирм).

39. Модель «Хищник-Жертва»

6

40. Модель «Хищник-Жертва»

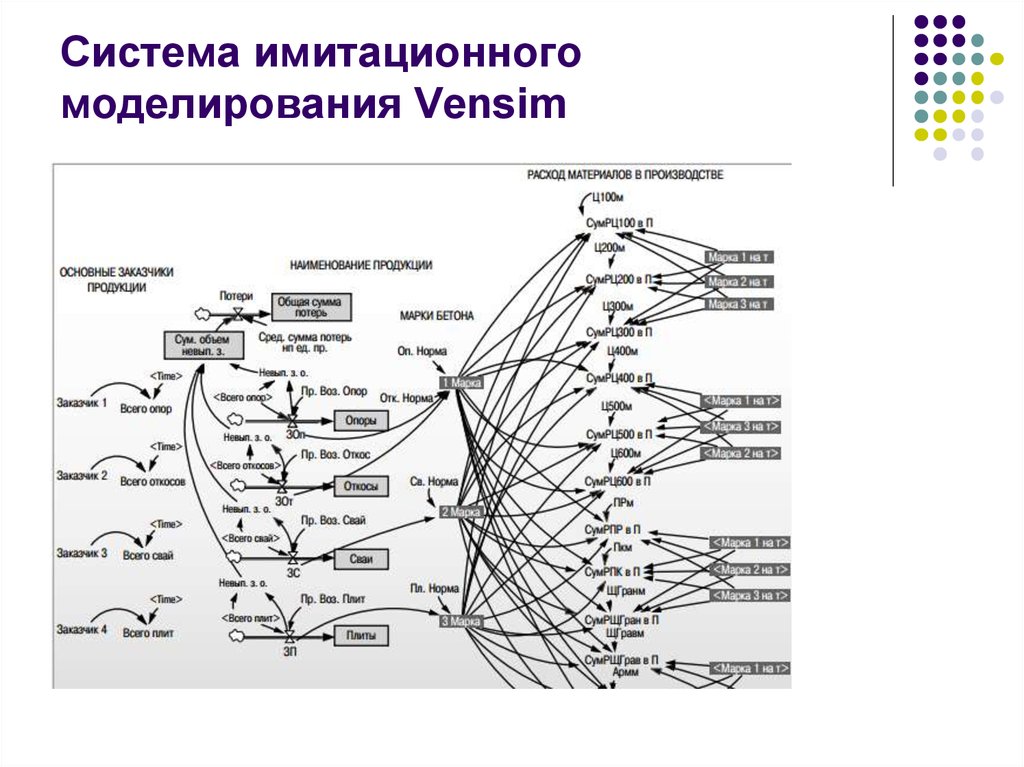
6

41. Система имитационного моделирования Vensim

42. Система имитационного моделирования GPSS

43. Список литературы

Емельянов А.А. Имитационное моделирование
экономических процессов.
Рыжиков Ю.И. имитационное моделирование.
Карпов Ю. Г. Имитационное моделирование систем.
Введение в моделирование с AnyLogic.
Труб И. Имитационное моделирование на СИ++.
Худякова Е.В., Липатов А.А.
Имитационное моделирование экономических
процессов в АПК. – М.: Издательский центр МГАУ,
2006.