Несобственные интегралы 1-го и 2-го рода. Лекция 14

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы
Екатерины II
Раздел: Определенный интеграл
Лекция 14.
Несобственные
интегралы 1-го и 2-го
рода
26.05.2025
г. СанктПетербург
2025
1/14

2.

Содержание лекции
1. Определение несобственных интегралов:
– I-го рода (с бесконечным пределом)
– 2-го рода (от неограниченной
функции).
2. Признаки сходимости несобственных
интегралов.
2|14

3.

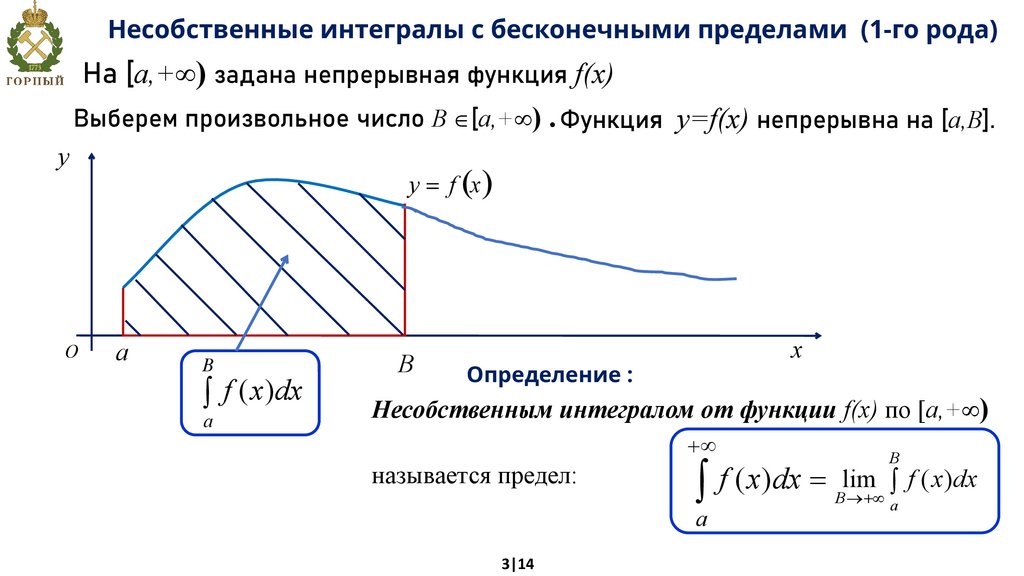
Несобственные интегралы с бесконечными пределами (1-го рода)
На [a,+ ) задана непрерывная функция f(x)
Выберем произвольное число B [a,+ ) . Функция y=f(x) непрерывна на [a,В].
y
O
y = f (x )
a
B
ò f ( x)dx
a
B
x
Определение :
Несобственным интегралом от функции f(x) по [a,+ )
+¥
называется предел:
lim
f
(
x
)
dx
f
(
x
)
dx
=
ò
ò
B ® +¥
a
3|14
B
a

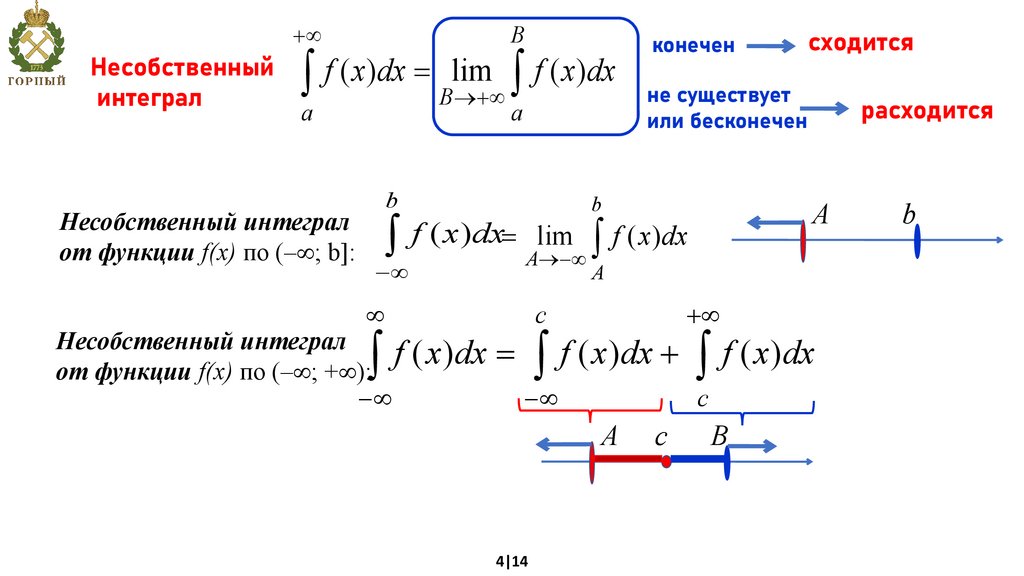
4.

Несобственный
интеграл
+¥
B
конечен
a
a
или бесконечен
f ( x)dx
ò f ( x)dx = Blim
ò
не существует
®+¥
Несобственный интеграл
от функции f(x) по (– ; b]:
b
b
-¥
A
+¥
c
ò
ò
расходится
А
f ( x)dx
ò f ( x)dx= Alim
ò
®-¥
¥
сходится
ò
Несобственный интеграл
f
(
x
)
dx
=
f
(
x
)
dx
+
f
(
x
)
dx
от функции f(x) по (– ; + ):
-¥
-¥
c
А
4|14
с
В
b

5.

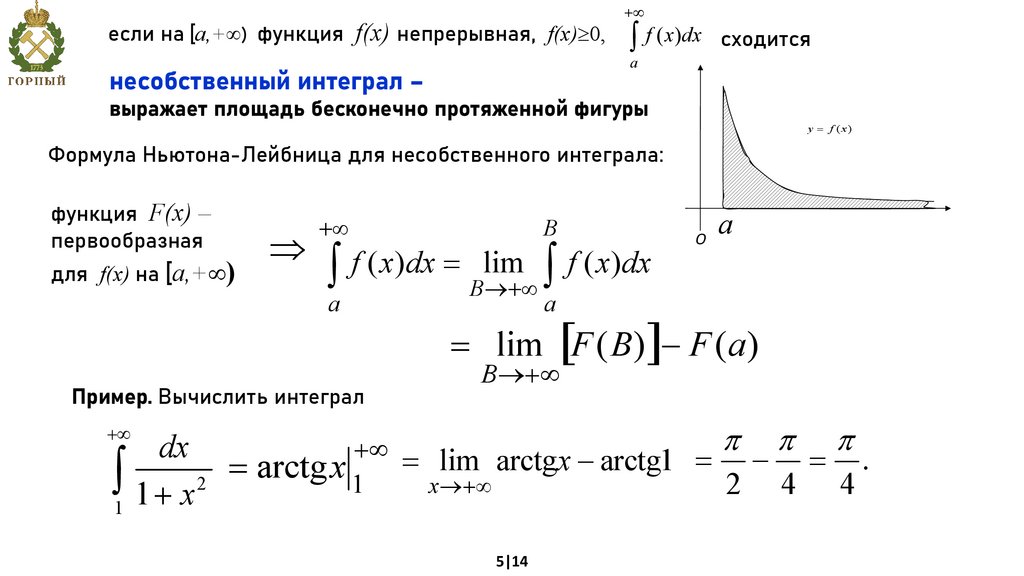
если на [a,+ ) функция f(x) непрерывная, f(x) 0,
+¥
ò f ( x)dx сходится
a
несобственный интеграл –
выражает площадь бесконечно протяженной фигуры
y = f ( x)
Формула Ньютона-Лейбница для несобственного интеграла:
функция F(x) –
первообразная
для f(x) на [a,+ )
Þ
+¥
B
a
a
f ( x)dx
ò f ( x)dx = Blim
ò
®+¥
Пример. Вычислить интеграл
O
a
= lim [F ( B )]- F (a )
B ®+¥
dx
+¥ = lim arctgх - arctg1 = p - p = p .
ò1 1 + x 2 = arctgx 1 х®+¥
2 4 4
+¥
5|14

6.

dx
сходится при р > 1
ò p (a > 0)
расходится при p £ 1
a x
+¥
Исследовать на
сходимость интеграл
+¥
+¥
dx
ò xp =
a
p =1
dx
+
ò x = ln x a
a
+¥
р 1
òx
a
-p
= lim (ln х - ln a ) = +¥
х®+¥
р>1
1
1 + 1 æ
1
1 ö
dx =
- p -1 ÷ =
p
1
1 - p х p -1 a = 1 - p çè хlim
®+¥ х
а
ø р<1
Пример. Вычислить несобственный
интеграл или доказать его
раcходимость:
+¥
B
-x
xe
ò
ò xe dx = Blim
®+¥
0
0
-x
)
0
(e
-B
)
-1
6|14
( p - 1)a p -1
= +¥
ìïu = x, du = dx,
üï
dх =í
-x
-x ý
ïîdv = e dх, v = -e ïþ
Bö
B B
é
ù
æ
B
= lim ê - xe- x + ò e- x dx ú = lim çç - B - e - x ÷÷ = - lim 1 + 1 = 1
В ®+¥ ê
0 0
úû B®+¥ è e
0ø
B ®+¥ e B
ë
(
=
1
у
у = хе–
х
0
B→∞
х

7.

+¥
ò f ( x)dx абсолютно сходится, если сходится ò f ( x) dx
Несобственный
интеграл
Если интеграл
+¥
+¥
a
a
+¥
ò f ( x)dx сходится, а ò f ( x) dx расходится,
a
+¥
то интеграл
Признак сходимости:
a
ò f ( x)dx называется условно сходящимся.
a
+¥
ò f ( x)dx абсолютно сходится интеграл сходится
a
Признак сравнения:
Если на [a,+ ) функции f(x) и g(x) непрерывны и удовлетворяют условию 0 g(x) f(x),
+¥
то из сходимости интеграла
+¥
из расходимости
ò g ( x)dx
+¥
ò f ( x)dx следует сходимость интеграла ò g ( x)dx ;
a
+¥
следует расходимость ò f ( x) dx .
a
a
7|14
a

8.

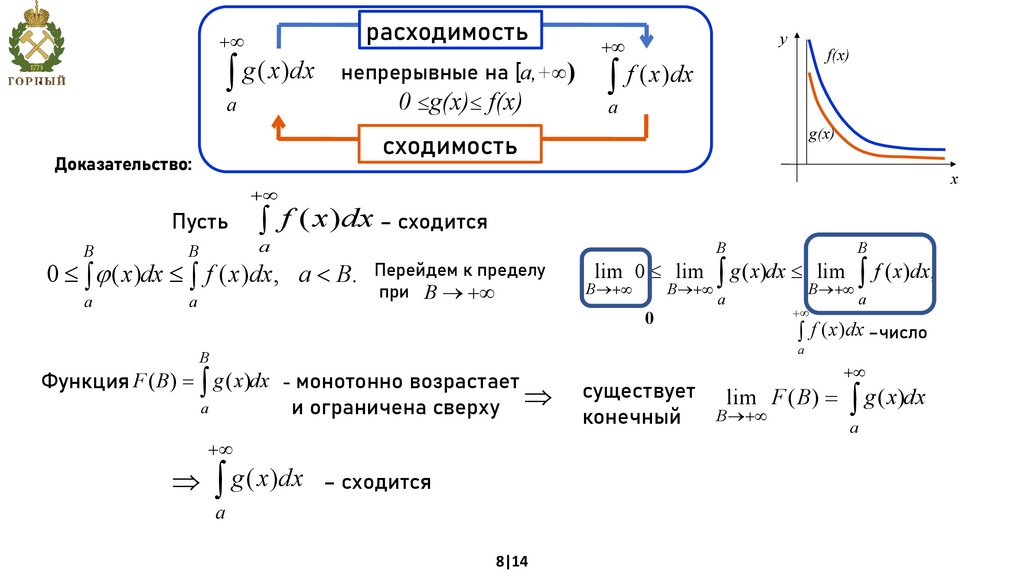
расходимость
+¥
y
+¥
f(x)
ò g ( x)dx непрерывные на [a,+ ) ò f ( x)dx
0 g(x) f(x)
.
a
a
g(x)
сходимость
Доказательство:
x
+¥
Пусть
B
B
a
a
ò f ( x) dx – сходится
a
0 £ ò j ( x)dx £ ò f ( x)dx, a < B. Перейдем к пределу
при B ® +¥
B
B
lim 0 £ lim ò g ( x)dx £ lim ò f ( x)dx,
B ®+¥
B ®+¥
B ®+¥
a
+¥
0
a
ò f ( x)dx –число
a
B
Функция F ( B) = ò g ( x)dx - монотонно возрастает
a
и ограничена сверху
+¥
ò g ( x)dx
– сходится
a
8|14
существует
конечный
+¥
lim F ( B) = ò g ( x)dx
B ®+¥
a

9.

Признак сравнения в предельной форме:
Если на [a,+ ) функции f(x) и g(x) непрерывны и неотрицательны,
f ( x)
= K (0 < K < +¥) ,
существует конечный предел lim
x®+¥ g ( x )
+¥
+¥
a
a
тогда оба интеграла ò f ( x ) dx
Доказательство.
ò g ( x)dx либо сходятся, либо расходятся одновременно.
f ( x)
f ( x)
f ( x)
K
<
e
-K <e
-e <
lim
= K g ( x)
x®+¥ g ( x )
g ( x)
+¥
Если ò f ( x ) dx
– сходится
a
+¥
g ( x)( K - e ) < f ( x) < g ( x)( K + e )
+¥
+¥
a
a
ò ( K - e ) g ( x)dx = ( K - e ) ò g ( x)dx – сходится
ò g ( x)dx – сходится
a
9|14

10.

Примеры. Исследовать сходимость несобственные интегралы:
+¥
sin x
dx.
1. ò
2
1+ x
1
+¥
2. ò
1
dx
3
x +1
+¥
sin x
1
x Î [1, + ¥ ) 0 £
£
,
2
2
1+ x
1+ x
dx
ò1 1 + x 2 – сходится
интеграл сходится абсолютно
.
при х 1
1
3
x +1
<
1
x
+¥
dx
1
3
ò
3
x
+¥
= ò
1
интеграл сходится
dx
x
3/ 2
– сходится
интеграл сходится по признаку сравнения
d (arctg x)
+¥
2 +¥
2
arctg x
(arctg
x
)
p
dx = arctg x d (arctg x) =
3. ò
=
2
ò
8
0 1+ x
2
+¥
0
0
+¥
1
dx
Доказать, что интеграл ò
2
-¥ 1 + x + x
сходится и вычислить этот интеграл
10|14

11.

Несобственный интеграл от неограниченной функции (II-го рода)
функция f(x) непрерывна на [a,b), а в окрестности
точки b не ограничена, т.е.
lim f ( x) = ±¥
x ®b - 0
b
b -e
конечен
сходится
a
a
или бесконечен
расходится
f ( x)dx
ò f ( x)dx = elim
ò
не существует
®0
Если на (a,b]
lim f ( x) = ±¥ , то
x ®a + 0
Функция f(x) не ограничена
в точке с (а < с <b):
b
f
(
x
)
dx
=
lim
ò
d ®0
a
b
c
b
a
a
c
y
x
a
b
f
(
x
)
dx
ò
a +d
ò f ( x)dx = ò f ( x)dx + ò f ( x)dx.
11|14
b

12.

Формула Ньютона-Лейбница:
функция F(x) –
первообразная
b
b -e
a
a
f ( x)dx = lim [F (b - e )]- F (a )
Þ ò f ( x)dx = elim
ò
®0
e ®0 +
для f(x) на [a,b)
Понятие абсолютной сходимости для несобственного интеграла от
неограниченной функции определяется аналогично
Пример. Вычислить интеграл
dx
dx
= lim ò
ò
e ®0
1 ( x - 1) x + 3
1+e ( x - 1) x + 3
6
6
3
= lim 2 ×
e ®0 +
ò
2
x = t - 3;
dx = 2tdt
x = 1+ e Þ t = 4 + e
x=6Þ t =3
1 æç 1
4 + e - 2 ö÷
=
ln - lim ln
2 çè 5 e ®0
4 + e + 2 ÷ø
dt
2
t
-4
4 +e
1
t-2
ln
2× 2 t + 2
x + 3 = t2;
3
4 +e
12|14
3
= lim
e ®0 +
ò (t 2 - 4)t
4 +e
0
= +¥
2t dt
интеграл
расходится

13.

Исследовать на сходимость несобственный интеграл
3< x£5
x cos x = x cos x £ x
5
ò
3
x
x cos x
x2 - 9
t = x 2 - 9; x = 5 Þ t = 16
£
16
13|14
x cos x
3
x2 -9
ò
dx
x
x2 - 9
1
dt
1
dx =
= ò
= 2 t
2
x -9
20 t 2
dt = 2 xdx x = 3 Þ t = 0
интеграл сходится по признаку сравнения
5
16
0
=4
Несобственный
интеграл
сходится

14.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы Екатерины
II
14|14