Similar presentations:
Несобственные интегралы. Лекция 15
1.
Несобственныеинтегралы
Лекция 15
2.
bПри определении определенного интеграла f x dx мы предполагали, что:
a
1) отрезок интегрирования a, b – конечный,
2) функция f x непрерывна на отрезке a, b .
Если не выполняется хотя бы одно из этих условий, то интеграл
называется несобственным.
§1. Несобственные интегралы с бесконечными
пределами интегрирования
Определение: Пусть функция f x непрерывна на интервале a; . Тогда,
если существует (конечный или бесконечный) предел
b
lim f x dx ,
b
a
то его называют несобственным интегралом от функции f x на интервале
a, и обозначают
f x dx
a
3.
Следовательно, по определению имеем:b
f x dx lim f x dx
b
a
(1.1)
a
В случае, если этот предел конечен, говорят, что интеграл (1.1) сходится,
если же предел (1.1) бесконечен или вовсе не существует, то говорят, что
несобственный интеграл расходится.
Аналогично определяются несобственные интегралы и для других
бесконечных интервалов:
b
b
f x dx lim f x dx (1.2)
a
a
c
c
f x dx f x dx f x dx , (1.3)
где с - любая фиксированная точка оси OX.
Несобственный интеграл f x dx сходится тогда, когда сходится каждый
из несобственных интегралов в правой части равенства (1.3).
4.
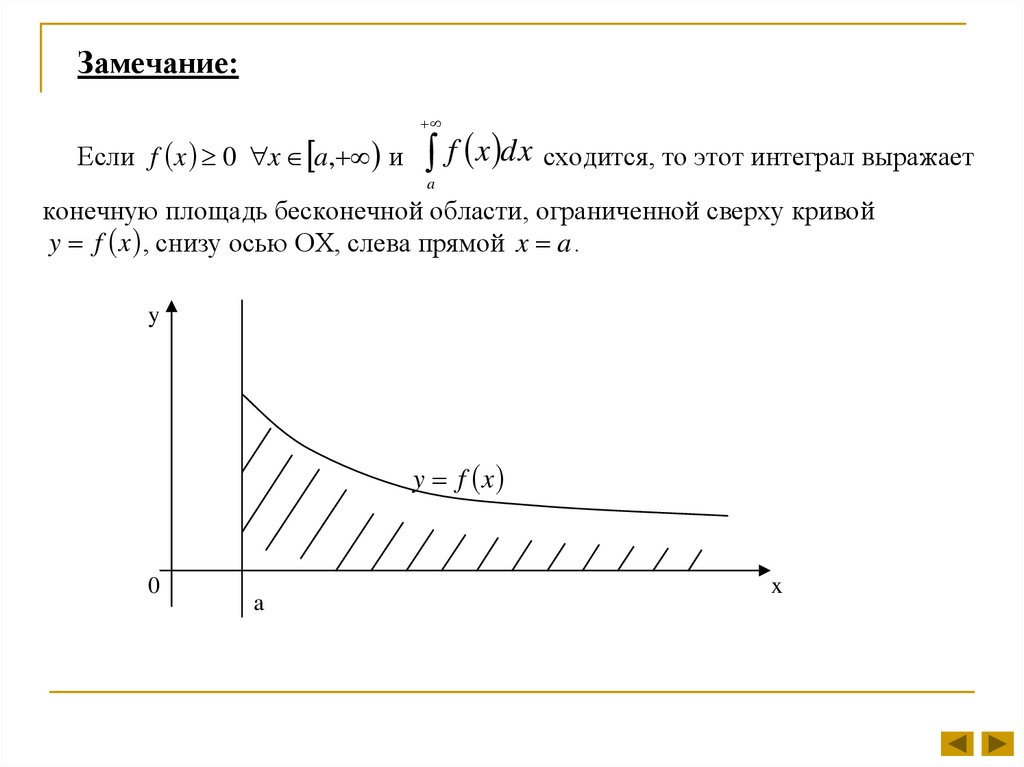
Замечание:Если f x 0 x a, и
f x dx сходится, то этот интеграл выражает
a
конечную площадь бесконечной области, ограниченной сверху кривой
y f x , снизу осью OX, слева прямой x a .
y
y f x
0
a
x
5.
Примеры. Вычислить:b
dx
dx
1 b
1
lim
lim
lim
1 1
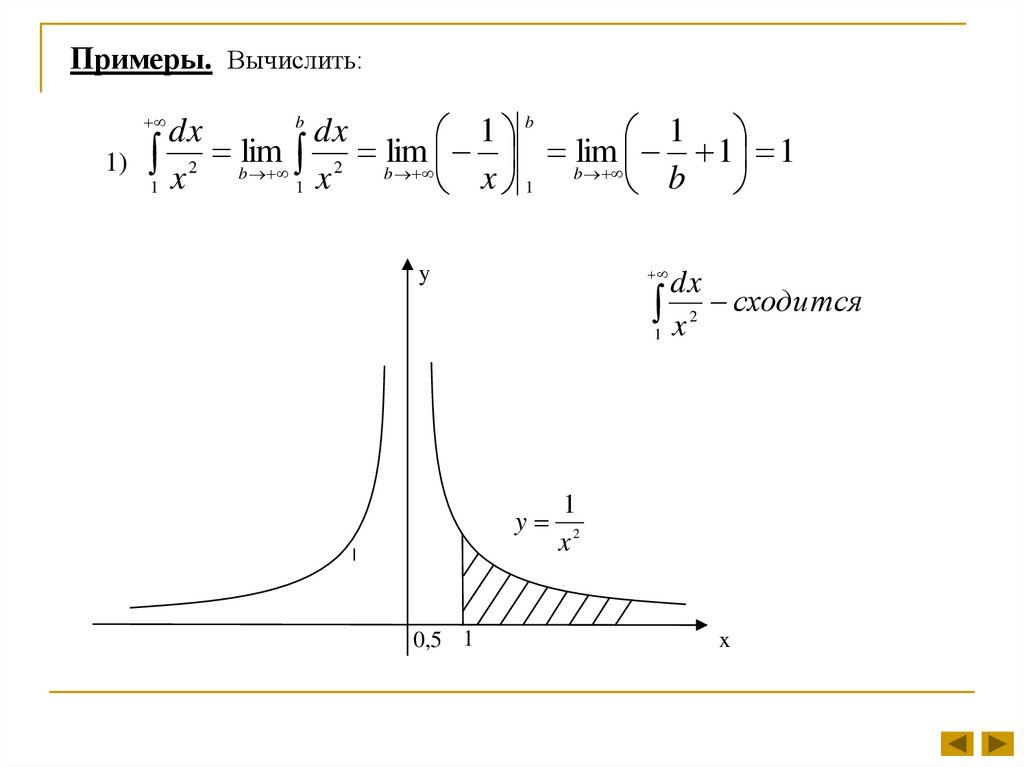
1) 2
2
b
b
b
x 1
b
1 x
1 x
y
dx
1 x 2 сходится
y
0,5 1
a
1
x2
x
6.
0dx
dx
dx
2)
0 1 x 2
2
2
1 x
1 x
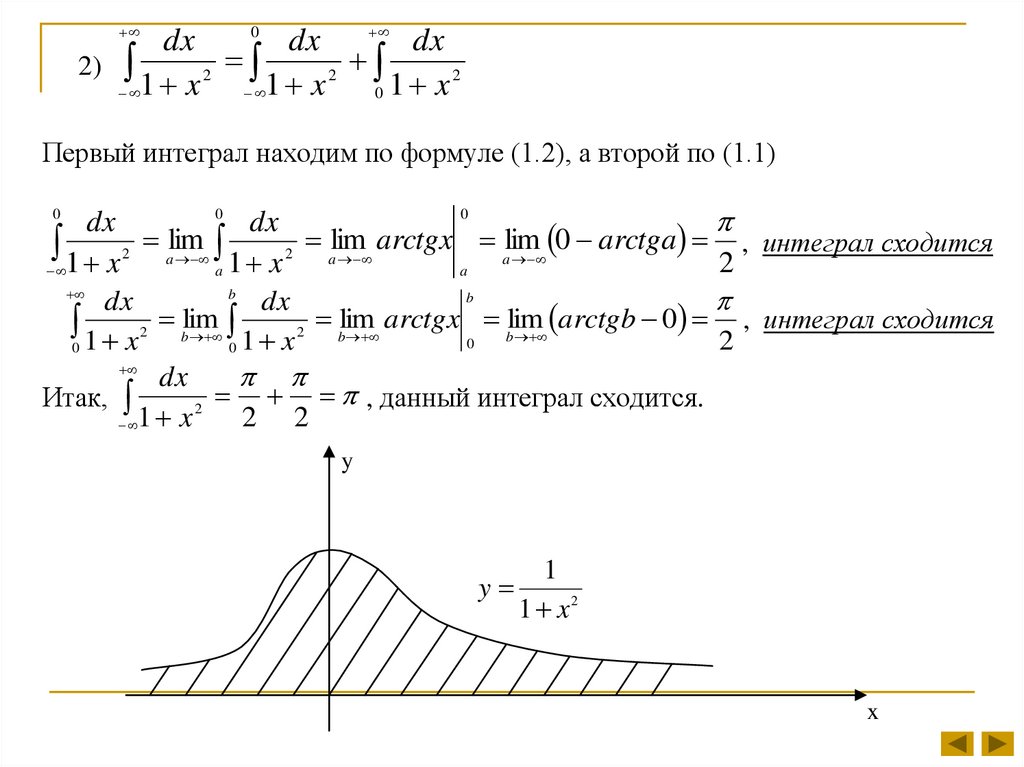
Первый интеграл находим по формуле (1.2), а второй по (1.1)
0
0
dx
dx
lim
lim
arctgx
lim
0
arctga
, интеграл сходится
1 x 2 a a 1 x 2 a
a
2
a
b
b
dx
dx
0
1 x lim 1 x lim arctgx lim arctgb 0 2 , интеграл сходится
2
0
b
2
0
b
0
b
dx
, данный интеграл сходится.
Итак,
2
2 2
1 x
y
y
1
1 x2
x
7.
bb
dx
dx
ln b ln 1 blim
ln x blim
blim
blim
ln b
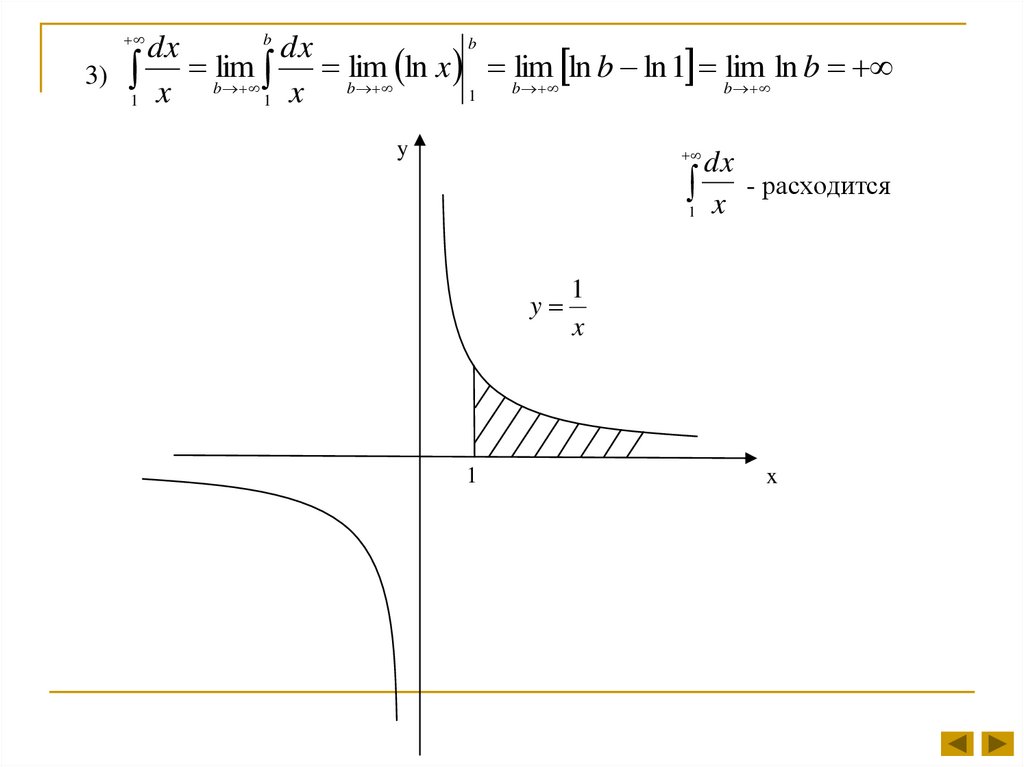
3)
1
1 x
1 x
y
dx
1 x - расходится
y
1
a
1
x
x
8.
bb
0
0
0
cos xdx blim
sin x blim
sin b - не существует
4) cos xdx blim
cosxdx - расходится
0
§2. Признаки сходимости несобственных интегралов с
бесконечными пределами интегрирования
Иногда бывает достаточно установить сходимость несобственного
интеграла, не вычисляя его значения. Для этого можно воспользоваться
следующими признаками сходимости.
►Теорема 1(признак сравнения).
Пусть при x a выполняются неравенства: 0 f ( x) ( x) . Тогда:
1) если
2) если
a
a
( x)dx сходится, то сходится и интеграл f ( x)dx ;
a
a
f ( x)dx расходится, то расходится и интеграл ( x)dx .
9.
Примеры:1) Исследовать сходимость интеграла
dx
1 x3e x .
1
1
Так как 3 x 3
xe
x
при
x 1
2 b
dx
x
1
1
1
3
x dx lim
lim 2 1 сходится.
1 x3 blim
b 2 1
2 b b
2
1
b
dx
dx
т.к. x 3 сходится, x 3e x - сходится.
1
1
10.
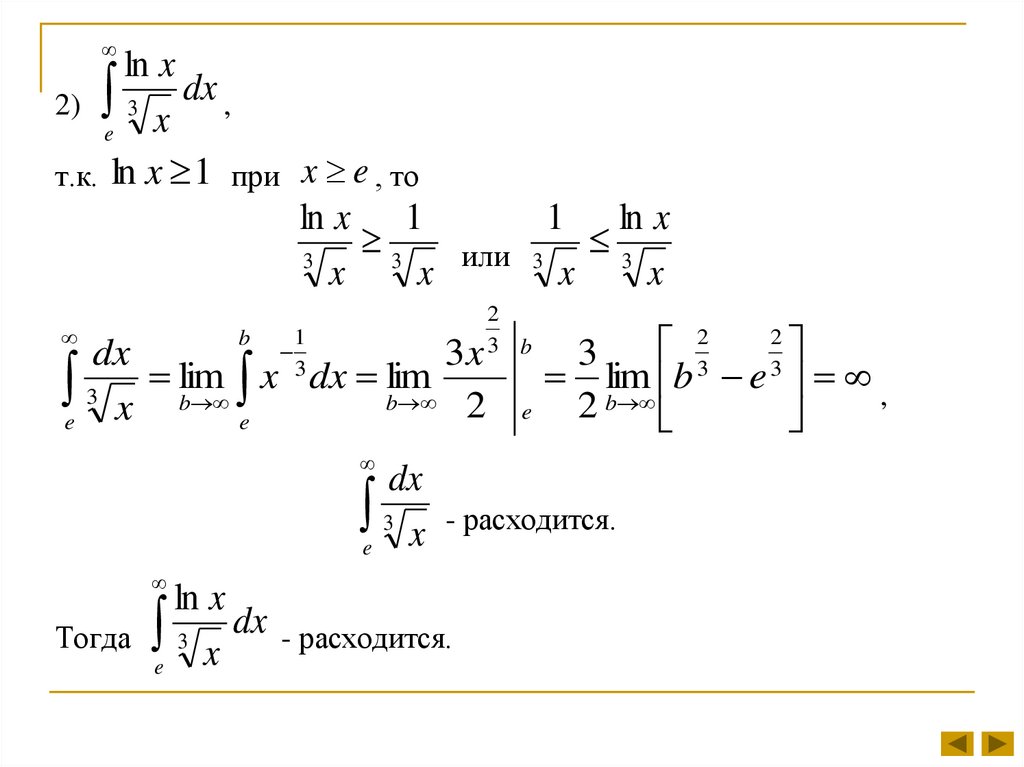
ln x2) 3 dx ,
x
e
т.к. ln x 1 при x e , то
ln x 1
1 ln x
3
или 3 3
3
x
x
x
x
2
3 b
2
2
dx
3x
3
3
3
x dx lim
lim b e ,
e 3 x lim
b
b 2
2 b
e
e
b
1
3
dx
e 3 x - расходится.
ln x
Тогда 3 dx - расходится.
x
e
11.
►Теорема 2. Пусть приТогда, если
x a верно неравенство:
f ( x) ( x) , ( ( x) 0)
a
a
( x)dx сходится, то сходится и интеграл f ( x)dx .
►Определение.
f ( x)dx
Несобственный интеграл
называется абсолютно
a
сходящийся, если сходится
f ( x) dx.
a
Несобственный
интеграл
f ( x)dx
называется
a
сходящийся, если он сходится, а
f ( x) dx - расходится.
a
условно
12.
cos xdx .
3
Пример: Исследовать на абсолютную сходимость:
x
1
cos x
dx ,
Составим x 3
1
dx 1
1 x 3 2 - сходится.
Значит,
cos x
1 x 3 dx - сходится (по признаку сравнения).
cos x
dx - абсолютно сходящийся.
Следовательно,
3
x
1
Замечание. На практике иногда сходимость несобственных интегралов
устанавливают с помощью следующего признака:
Интеграл f ( x)dx
(a>0)
a
M
и m>1
xm
M
f ( x) m и m 1 , M,m=const.
x
сходится, если f ( x)
расходится, если
13.
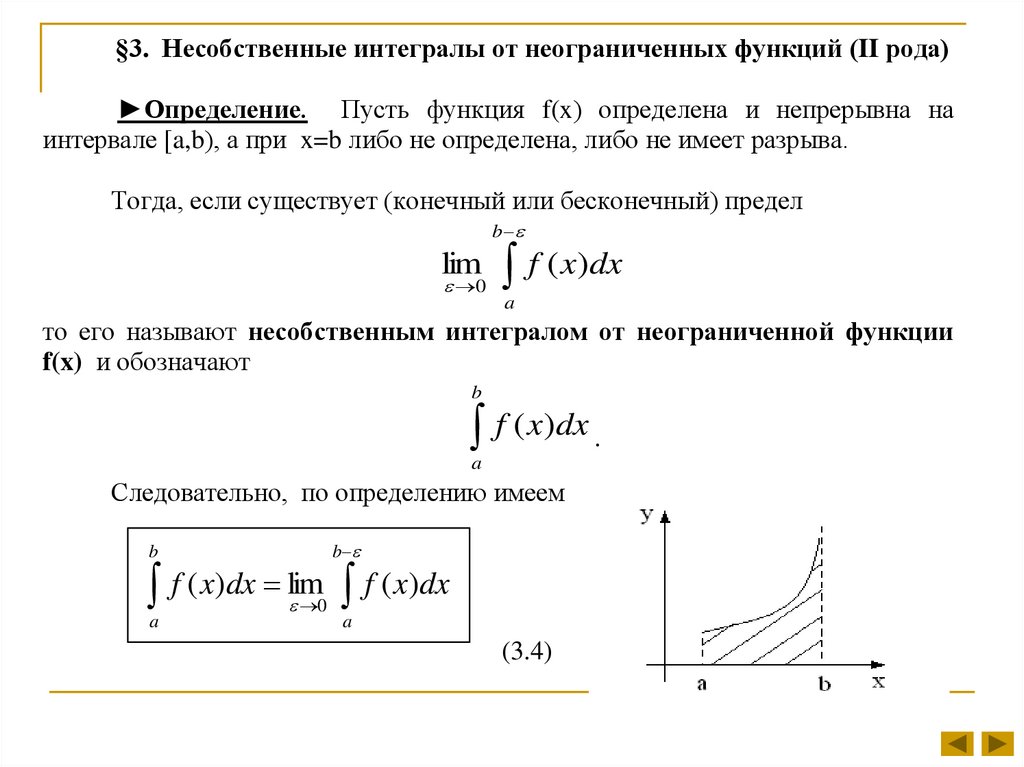
§3. Несобственные интегралы от неограниченных функций (II рода)►Определение. Пусть функция f(x) определена и непрерывна на
интервале [a,b), а при x=b либо не определена, либо не имеет разрыва.
Тогда, если существует (конечный или бесконечный) предел
b
lim f ( x)dx
0
a
то его называют несобственным интегралом от неограниченной функции
f(x) и обозначают
b
f ( x)dx .
a
Следовательно, по определению имеем
b
b
f ( x)dx lim
f ( x)dx
a
0
a
(3.4)
14.
В случае, если этот предел конечен, говорят, что интеграл (3.4)сходится, если же предел (3.4) бесконечен или не существует, то говорят,
что интеграл (3.4) расходится.
Аналогично, если функция f(x) разрывна или не определена при x =
a, то
b
b
f ( x)dx
f ( x)dx lim
0
a
(3.5)
a
При x = с , где c ( a, b)
c
b
b
f ( x)dx lim f ( x)dx
f ( x)dx lim
a
0
a
0
b
Интеграл
f ( x)dx в (3.6) сходится тогда,
a
когда существуют конечные пределы в правой части.
c
(3.6)
15.
Примеры:1)
1
1
1
dx
dx
lim 2 x 2 lim (1 ) 2
x lim
0
0
x 0
0
- интеграл сходится.
1
2)
1
dx
1 x lim
0
2
0
0
dx
1 x
2
lim (arcsin x)
lim arcsin( 1 ) arcsin 0
0
1
0
2 - интеграл сходится.
2
1
2
x 1
dx
dx
dx
3) x 1 беск. разрыв x 1 x 1 ;
1
1
1
0
1
1
1
dx
dx
lim
ln x 1
1 x 1 0 1 x 1 lim
0
1
1
dx
lim ln ln 2 .
- расходится,
0
x
1
1
2
dx
следовательно, x 1 - расходится.
1
16.
§4. Признаки сходимости несобственных интегралов отнеограниченных функций
►Теорема 3. Пусть при x a, b выполнены неравенства 0 f ( x) ( x)
и функции f (x ) и (x ) либо не определены, либо имеют разрыв при x b .
Тогда
1) если
2) если
b
b
a
a
( x)dx сходится, то сходится и f ( x)dx .
b
b
a
a
f ( x)dx расходится, то расходится и ( x)dx
►Теорема 4. Пусть при x a, b выполнено неравенство:
f ( x) ( x), ( x ) 0 ,
а функции f (x ) и (x ) либо не определены, либо имеют разрыв при x b .
Тогда если
b
b
a
a
( x)dx сходится, то и f ( x)dx сходится.










 mathematics
mathematics








