Обратная матрица, обращение матрицы

1. Обратная матрица, обращение матрицы

Грехов А.А. 2вб1

2. Определители

Определитель – есть числовое выражение
матрицы А. Любой квадратной матрице n-го
порядка можно поставить в соответствие
выражение, которое называется
определителем (детерминантом) матрицы

3. Детерминант матрицы

Если детерминант матрицы является нулем, то обратную к ней матрицу
нельзя получить.

4. Формула для вычисления обратной матрицы 1)

!

5. Пример

Нахождение обратной матрицы через алгебраические дополнения
Пример
Нужно найти обратную матрицу для следующей матрицы:
Решение:
Далее нам нужно найти алгебраические дополнения.

6. Алгебраические дополнения

Формула

7. Задание

1) Найти определитель, главное что он не равен 0
2) Найти для каждого элемента свой минор
3) Подставить в формулу и найти каждый элемент матрицы
4) Транспортировать матрицу
5) Написать обратную матрицу
6) Выполнить проверку

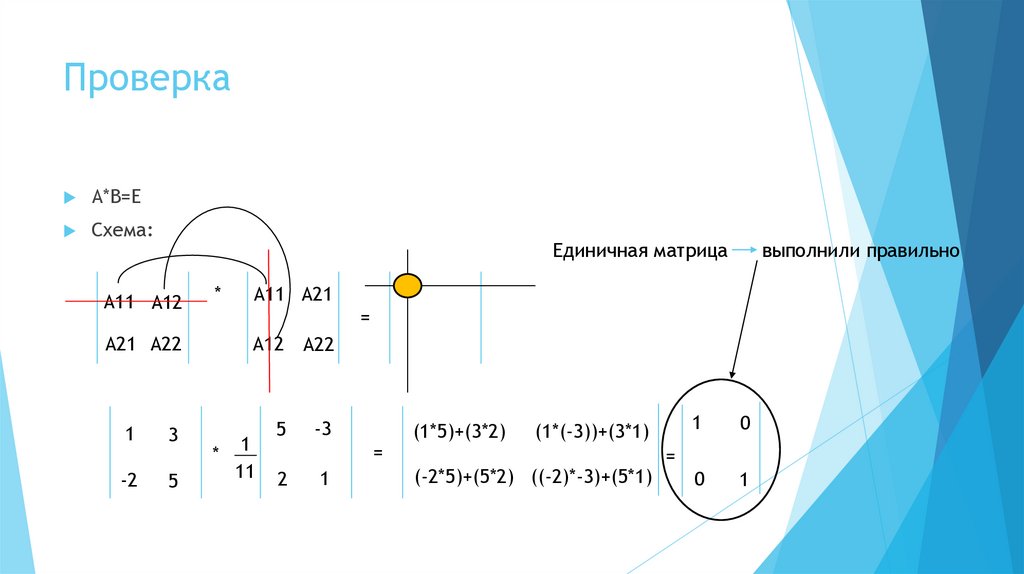
8. Проверка

A*B=E
Схема:
Единичная матрица
A11 A12
*
A11 A21
=
A21 A22
A12 A22
1
5
-2
3
5
выполнили правильно
*
1
11
-3
=
2
1
(1*5)+(3*2)
(1*(-3))+(3*1)
(-2*5)+(5*2) ((-2)*-3)+(5*1)
1
0
0
1
=

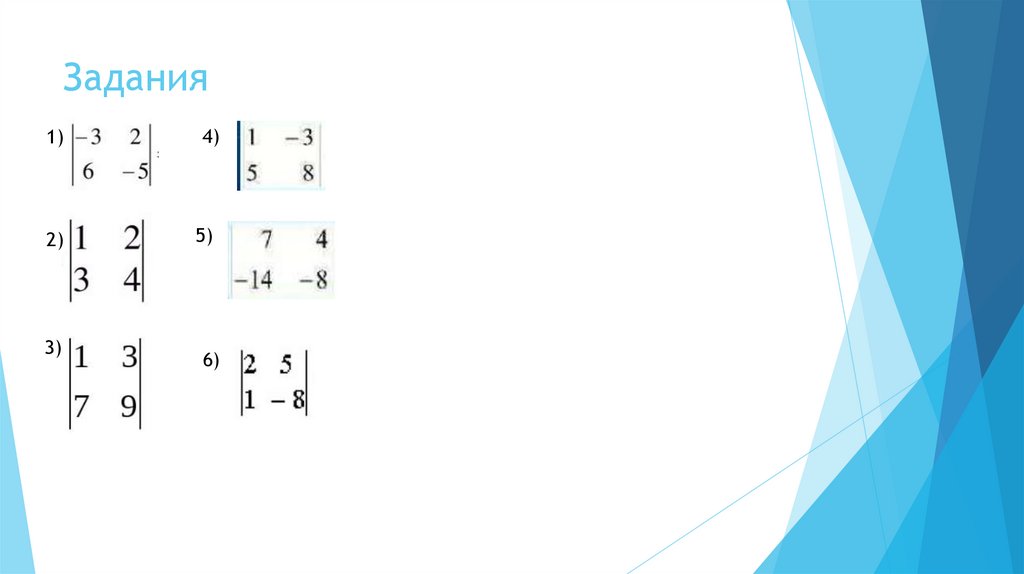
9. Задания

1)
4)
2)
5)
3)
6)

10. Задания

11. Задания