Similar presentations:
Обратная матрица
1. Обратная Матрица
2. Определение. Матрица называется о б р а т н о й к квадратной матрице , если
A B B A EОбратная матрица обозначается символом
1
1
A
1
A A A A E
Примечание. Операция деления для матриц не
определена. Вместо этого предусмотрена операция
обращения (нахождения обратной) матрицы.
3. Определение. Матрица, составленная из алгебраических дополнений для элементов исходной матрицы , называется с о ю з н о й м а т р и ц е й .
Определение. Матрица, составленная изалгебраических дополнений для элементов
исходной матрицы , называется
союзной матрицей.
A11
A A21
A
31
A12
A22
A32
A13
A23
A33
4. Формула для нахождения обратной матрицы
11
T
A
A
det A
5.
A11 A21 A311
1
A
A12 A22 A32
det A
A
A
A
13 23 33
6. Алгоритм нахождения
• 1. Находим определительматрицы А. Он должен быть
отличен от нуля.
• 2. Находим алгебраические
дополнения для каждого
элемента матрицы А.
• 3. Составляем союзную
матрицу и транспонируем ее.
• 4. Подставляем результаты
п.1 и п.4 в формулу обратной
матрицы.
A
1
7. Пример. Найти матрицу, обратную к матрице:
1 2A
4
3
8.
Р е ш е н и е. Действуем по алгоритму:1. Находим определитель матрицы:
1 2
det A =
3 4
= 4- 6 = - 2
Определитель отличен от нуля det A № 0 ,
следовательно, обратная матрица существует.
9.
2. Находим алгебраические дополнения:10.
A11 = 4A21 = - 2
A12 = - 3
A22 = 1
11.
3. Составляем союзную матрицу:~ 4 3
A
2 1
12.
4. Записываем обратную матрицу поформуле
1
T
1 4
A
A
2 3
det A
1
2
1
13. 5. Проверка
• Воспользуемся определением обратнойматрицы и найдем произведение
1
A A
1 4 2 1 2
2 3 1 3 4
1 4 1 2 3 4 2 2 4 1 2 0 1 0
2 0 2 0 1
2 3 1 1 3 3 2 1 4
14. Задача. Найти матрицу, обратную к данной
2 1 1A 3 2 1
1 2 1
15. 1. Находим определитель
2 1 1det A 3 2 1 2 2 1 3 2 1 1 1 1
1 2 1
1 2 1 1 2 2 3 1 1
4 6 1 2 4 3 3 5 2 0.
16. 2. Алгебраические дополнения для первой строки:
2 1A11
2 2 4,
2 1
3 1
A12
3 1 2,
1 1
3 2
A13
6 2 8,
1 2
17. Алгебраические дополнения для второй строки:
1 1A21
1 2 1,
2 1
2 1
A22
2 1 1,
1 1
2 1
A23
4 1 3,
1 2
18. Алгебраические дополнения для третьей строки:
1 1A31
1 2 3,
2 1
2 1
A32
2 3 1,
3 1
2 1
A33
4 3 7.
3 2
19. Обратная матрица:
4 1 31
1
A 2 1 1
2
8
3
7
20. Элементарные преобразования матриц
• перестановка строк (столбцов) местами;• исключение из матрицы строк (столбцов),
состоящих из нулей;
• умножение всех элементов какой-либо строки
(столбца) матрицы на любое число, отличное от
нуля;
• прибавление к одной строке (столбцу) другой,
предварительно умноженной на любое число,
отличное от нуля.
21.
Определение. Э к в и в а л е н т н ы м и называютсяматрицы, полученные одна из другой путем элементарных
преобразований.
Важным понятием для матриц является понятие РАНГА.
Существует несколько определений этого понятия. Мы
остановимся на одном из них, основанном на элементарных
преобразованиях.
Определение. Р а н г о м м а т р и ц ы называется
число ненулевых строк в матрице, после приведения ее к
ступенчатому виду (путем элементарных преобразований).
Обозначение. Ранг матрицы будем обозначать r ( A)
или
rang ( A)
.
Теорема. Ранг матрицы не меняется при элементарных
преобразованиях.




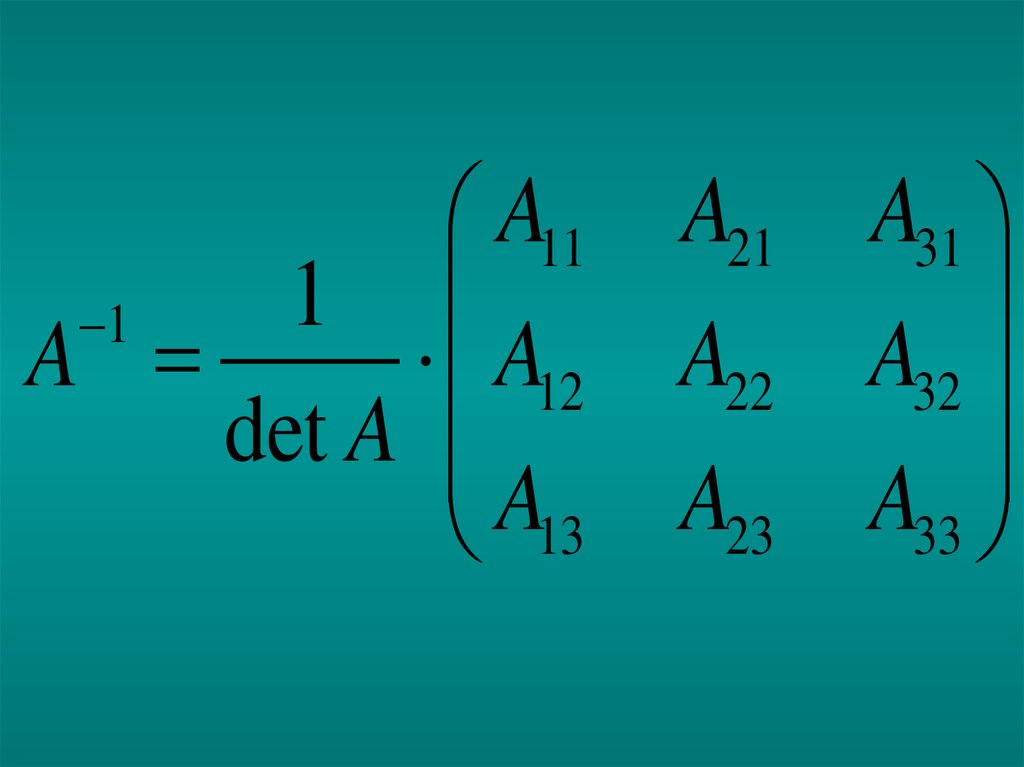




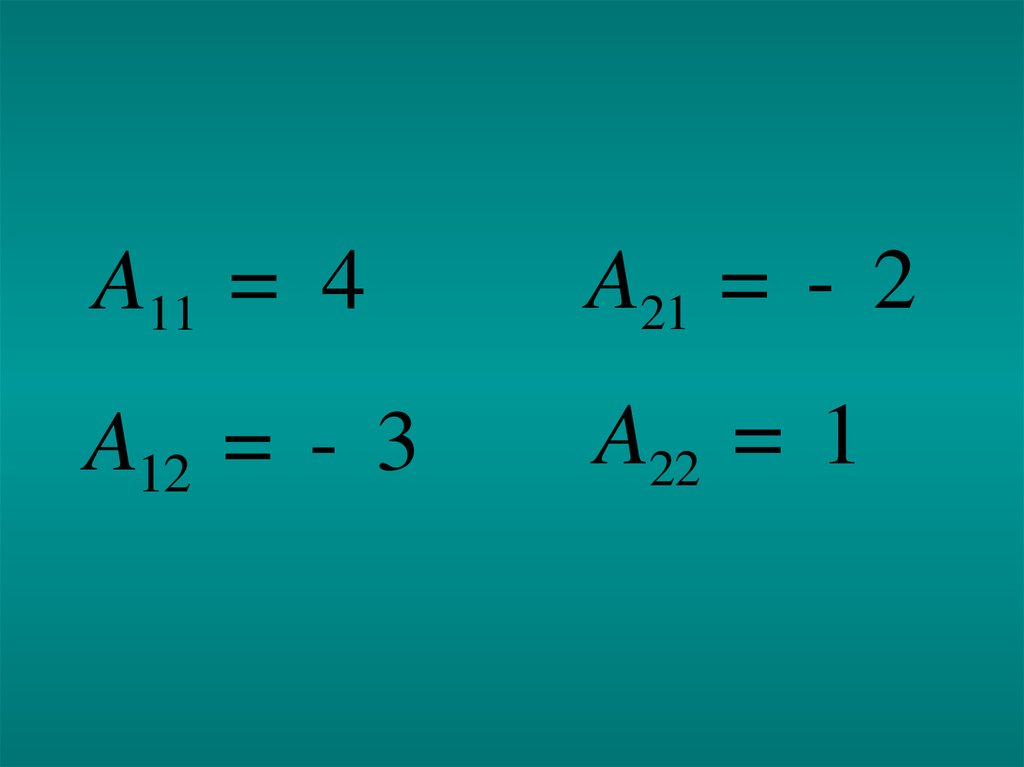











 mathematics
mathematics








