Similar presentations:
Матрицы и определетели
1.
Лекция № 1Матрицы и
определители
2. План лекции
Определение матрицы. Виды матриц.Линейные операции над матрицами.
Умножение матриц.
Определители второго и третьего порядков. Их свойства.
Обратная матрица.
Ранг матрицы.
3. Список литературы
Виленкин,И.В.
Высшая
математика
для
студентов
экономических, естественно-научных специальностей вузов:
учеб. пособие / И.В. Виленкин, В.М. Гробер. – Ростов н/Д:
Феникс, 2002.
Виленкин, И.В. Задачник по математике. Часть 1 / И.В.
Виленкин, О.Е. Кудрявцев, М.М. Цвиль, С.И. Шабаршина. –
Ростов н/Д: Российская таможенная академия, Ростовский
филиал, 2007.
Ермаков, В.И. Общий курс высшей математики для
экономистов: учебник / Под общ. ред. В.И. Ермакова – М.:
ИНФРА – М,2008.
Кремер, Н.Ш. Высшая математика для экономистов: учебник /
Н.Ш. Кремер, Б.А. Путко, И.М. Фридман. – М.: Банки и биржи,
ЮНИТИ, 2002.
4. Определение матрицы. Виды матриц.
Матрицейразмера m×n называется
прямоугольная таблица чисел, содержащая
m строк и n столбцов
a11 a12
a21 a22
A
am1 am 2
a1n
a2 n
amn
5.
Каждый элемент матрицы имеет дваиндекса: m – номер строки и n – номер
столбца. Например, в матрице
5 7 4 3
A 2
0 8 1
3 4 9 6
размера 3 4 , a11 5 , a23 8 , a34 6 .
Часто используется краткая запись матрицы:
A (aik ) m n
6.
Матрица называется квадратной n-гопорядка, если она состоит из n строк и n
столбцов.
Матрица
размера
1×n
называется
матрицей-строкой, а матрица размера m×1
матрицей-столбцом.
Нулевой матрицей 0 заданного размера
называется матрица, все элементы которой
равны 0.
7.
Единичнойназывается
квадратная
матрица, элементы главной диагонали
которой равны 1, а все остальные элементы
равны 0:
1
0
Е
0
0
1
0
0
0
1
8.
Транспонированной для матрицы Aназывается матрица AT, строки которой
являются столбцами матрицы , а столбцы –
строками . Например, если
3
5
5 9 4
T
A
A 9 2
3 2 1 , то
4
1
Матрицы A (aik )m n и B (bik ) m n называются
равными, если aik bik , i 1, , m , k 1, , n .
9. Линейные операции над матрицами.
Суммой матриц A (aik )m n и B (bik ) m nназывается матрица A B (aik bik ) m n .
Складываются
матрицы
только
одинакового размера.
10.
Например.Найти сумму и разность матриц А и В:
2 3 0
A
1 0 4
0 2 3
B
1 5 2
2 1 3
A B
2 5 6
2 5 3
A B
0 5 2
11.
Произведением матрицы А на число λназывается матрица A ( a ) .
Другими словами, для умножения матрицы
на число надо каждый элемент матрицы
умножить на это число. Любую матрицу
можно умножить на любое число.
ik
m n
12.
Например:Умножая матрицу
2 3 0
A
1 0 4
на число 2, получим:
2 2 3 2 0 2 4 6 0
A 2
1 2 0 2 4 2 2 0 8
13.
Для любых матриц одинакового размера илюбых чисел и выполняются свойства:
1. A B B A
2. A 0 A
3. A ( B C ) ( A B) C
4. ( A) ( ) A
5. ( A B) A B
6. ( ) A A A
14. Умножение матриц
Произведением матрицы A (aik ) m pматрицу B (bik ) p n
на
называется матрица C
p
размера m n с элементами cik aij b jk ,
j 1
i 1, 2, , m , k 1, 2, , n .
Другими словами, для получения элемента,
стоящего в i-той строке матрицы-произведения на kтом месте, следует вычислить сумму произведений
элементов i-той строки матрицы A на k-тый столбец
матрицы B.
15.
В самом определении произведения матрицзаложено, что число столбцов первой
матрицы должно совпадать с числом строк
второй.
Это условие согласования матриц при
умножении.
Если
оно
нарушено,
то
матрицы
перемножить нельзя.
Заметим, что вполне возможна ситуация,
когда A∙B существует, а B∙A нет.
16.
Приведем еще ряд свойств операцииумножения матриц. Если A, B и C квадратные матрицы одного порядка, то
справедливы равенства:
1. A ( B С ) ( A B) C
2. A ( B C ) A B A C
3. ( A B) C A C B C
4. A E E A A
17.
Пример.Найти произведение матриц:
2 3 0
A
1 0 4
1 0
B 1 4
0 2
Число столбцов первой матрицы равно числу строк
второй, следовательно их произведение существует:
2 1 3 1 0 0 2 0 3 4 0 2 5 12
A2 3 B3 2
1 1 0 1 4 0 1 0 0 4 4 2 1 8
18. Элементарные преобразования матрицы
1. Отбрасывание нулевой строки(столбца) матрицы.2. Умножение
всех элементов строки(столбца)
матрицы на число , неравное нулю.
3. Изменение порядка строк(столбцов)матрицы.
4. Прибавление
к каждому элементу одной
строки(столбца)
элементов
другой
строки
(столбца), умноженных на любое число.
5. Транспонирование матрицы.
19.
С помощью элементарныхпреобразований матрицу можно привести к
ступенчатому виду:
a11
0
A
...
0
где
a12
a22
...
0
...
...
...
...
a1r
a2 r
...
arr
...
...
...
...
a1k
a2 k
,
...
ark
aii 0, i 1,2,..., r; r k.
20. Обратная матрица
21.
22.
23.
24. Определители второго и третьего порядков. Свойства определителей
Понятие определителя вводится только дляквадратных матриц.
Определителем
(детерминантом)
матрицы n-го порядка называется
число:
a11 a12
a21 a22
n det A
... ...
an1 an 2
... a1n
... a2 n
... ...
... ann
25. Определители второго и третьего порядков. Свойства определителей
Рассмотрим квадратную матрицу 2гоa11 a12
порядка:
A
a
21
Определителем
называется число:
2го
a 22
порядка
матрицы
a11 a12
( A) A
a11a22 a12a21
a21 a22
A
26.
Определителем 3го порядка (матрицы)называется сумма произведений элементов
первой строки матрицы на их алгебраические
дополнения.
a11 a12
( A) A a21 a22
a31 a32
a11 a12
A a21 a22
a31 a32
a13
a23 a11 A11 a12 A12 a13 A13
a33
a13
a23 a11a22a33 a21a32a13 a12a23a31
a33 a a a a a a a a a
13 22 31
32
23 11
21 12 33
27.
Правило Сарруса:a11 a12
a21 a22
a31 a32
a13
a23
a33
a11 a12
a21 a22
a31 a32
a11a22a33 a12a23a31 a13a21a32
a13a22a31 a11a23a32 a12a21a33
28.
a113 a 21
a31
a12
a 22
a32
a13
a 23 a11a 22 a33 a 21a32 a13 a12 a 23 a31
a33
a a a a a a a a a
13 22 31
Правило треугольника:
«+»
«-»
32 23 11
21 12 33
29.
Например:4 3
1) Пусть A
.
2 5
Тогда
A 4 5 3 2 20 6 26.
2) Пусть
Тогда
2 3 4
A 5
6 7 .
1 4 8
6 7
5 7
5 6
A 2
3
4
2 20 3 47 4 26 285.
4 8
1 8
1 4
30.
Примеры:3)
3 2
3 5 2 1 15 ( 2) 17
1 5
4)
cos x sin x
cos 2 x sin 2 x cos 2 x
sin x cos x
5)
cos x sin x
2
2
cos x sin x 1
sin x cos x
31.
Примеры:5)
log 2 32 log 3 27
log 4 16 log 5 125
5 3
15 6 9
2 3
32.
Примеры:6)
4 7 2 4 7
3 1 5 3 1
5 0
7 5 0
4 ( 1) 7 7 5 5 ( 2) 3 0
5 ( 1) ( 2) 0 5 4 7 3 7
28 175 0 10 0 147 10
33.
Примеры:7)
4 7 2
3 1 5
5 0
7
4 ( 1) 7 7 5 5 ( 2) 3 0
5 ( 1) ( 2) 0 5 4 7 3 7
28 175 0 10 0 147 10
34. Свойства определителей
1. Определитель не меняется при транспонировании.2. Если
все элементы какой-либо строки (или
столбца) равны нулю, то определитель равен 0.
3. Если две строки (два столбца) поменять местами,
то определитель меняет знак.
4. Если элементы какой-либо строки (столбца)
содержат общий множитель, то его можно
вынести за знак определителя.
5. Если в определителе две строки (два столбца)
одинаковы
или
пропорциональны,
то
определитель равен 0.
35.
Если в определителе некоторая строка (столбец)представляет собой сумму двух слагаемых, то такой
определитель равен сумме двух определителей: в
первом определителе в выделенной строке (в
выделенном столбце) состоят первые слагаемые, а
остальные элементы не меняются; во втором
определителе в выделенной строке (в выделенном
столбце) состоят вторые слагаемые, а остальные
элементы не меняются.
6.
a11 b11
a21
a31
a12 b12
a22
a32
a13 b13 a11
a23
a21
a33
a31
a12
a22
a32
a13 b11
a23 a21
a33 a31
b12
a22
a32
b13
a23
a33
36.
a11a21
...
an1
a11
a21
...
an1
... a1 j
... a2 j
... ...
... anj
... a1 j b1 j
... a2 j b2 j
...
...
... anj bnj
... a1n
... a2 n
... ...
... ann
... a1n
a11
... a2 n
a21
... ...
...
... ann
an1
... b1 j
... b2 j
... ...
... bnj
... a1n
... a2 n
... ...
... ann
37.
2 1 42 2 1 4
2 2 4
2 1 4
7 2 3 7 3 1 3 7 3 3 7 1 3
7 5 5
7 2 3 5
7 2 5
7 3 5
60
38
98
38.
Определитель не изменится, если к элементамкакой-либо его строки (столбца) прибавить
элементы другой строки (столбца), умноженные на
одно и то же число.
8. Сумма произведений элементов любой строки
(столбца) на свои алгебраические дополнения равна
самому определителю.
9. Сумма произведений элементов любой строки
(столбца)
определителя
на
алгебраические
дополнения другой строки (столбца) равна 0.
7.
39.
Числовая иллюстрация свойств:1 свойство
3 5 8
A 1
4
9
7
2 634;
10
3
1
4
T
A 5 9 7 634 .
8 2 10
40.
Числовая иллюстрация свойств:2 свойство:
1 2 3
0 0 0
1 3
1 2
2 3
0.
0 0 0 1 2 3 0
0
0
7 5
7 8
8 5
7 8 5
7 8 5
41.
Числовая иллюстрация свойств:3 свойство:
3 5 8
1 3 2 3 23 5 11 8 5 164.
4 7
3
4 7
3
1 3 2 4 34 7 2 3 14 164.
3 5 8
42.
Числовая иллюстрация свойств:5 свойство:
1 2 3
1 2 3 1 14 2 17 3 16 0.
4 8 5
43.
Числовая иллюстрация свойств:4 свойство:
2 1
1
2
1
1
2 1 1
21 42 63 21 1 21 2 21 3 21 1 2 3
3
4
2
3
4
2
3 4 2
21 2 ( 8) 1 ( 11) 1 10 357.
44.
Числовая иллюстрация свойств:6 свойство:
12 1
2
7 5 3 2 5 3 7 3
5
5 2 3
7
3
5 7
3
5 7 3
5 7 3
5 .
5 2 3
5
2
3
5 2 3 5 2 3
45.
Числовая иллюстрация свойств:1 2 3
1
2
3
1
2
3
2 5 4
2
5
4
2
5
4
8 11 6 2 1 3 2 2 2 3 5 2 3 3 4 2 1 2 2 2 3
1 2
3
1 2 3
1 2 3
2
5
4 2 2 5 4 3 2 5 4 2 0 3 0 0.
3 2 3 5 3 4
1 2 3
2 5 4
46. Миноры и алгебраические дополнения
a11 a12Пусть A a21 a22
a
31 a32
a13
a23 − матрица 3го порядка.
a33
Минором элемента aik
называется
определитель
Mik,
составленный
из
элементов, оставшихся после вычеркивания
из матрицы i-той строки и k-того столбца.
Алгебраическим дополнением элемента aik
называется число
Aik ( 1) i k M ik .
47.
a11 a12det A A a21 a22
a31 a32
a13
a23
a33
a21 a23
M12
a31 a33
a11 a12
det A A a21 a22
a31 a32
a13
a23
a33
a11 a12
M 23
a31 a32
48. Для данного определителя найти миноры: М22, М31,М43
1 23
0 1 5
3 2 1
1 1 3
4
2
4
2
2
3 4
M 31 1 5 2 36
1 3 2
1 3 4
M 22 3 1 4 28
1 3 2
1 2 4
M 43 0 1 2 16
3 2 4
49.
Aij 1i j
a11 a12
A a21 a22
a31 a32
a13
a23
a33
M ij
a21 a23
M 12 1
a31 a33
A12 1
1 2
A22 1
2 2
a11 a13
M 22
a31 a33
50.
Теорема. Если в определителе порядкаn все элементы некоторой строки
(столбца) кроме одного элемента равны
нулю, то этот определитель равен
произведению этого отличного от нуля
элемента
на
его
алгебраическое
дополнение.
Теорема. Определитель равен сумме
произведений элементов любой строки
(или столбца) на свои алгебраические
дополнения.
51.
разложение по i-ой строке:n
A ai1 Ai1 ai 2 Ai 2 ... ain Ain aik Aik , i 1,..., n
k 1
разложение по j-ому столбцу:
n
A a1 j A1 j a2 j A2 j ... anj Anj akj Akj ,
k 1
j 1,..., n
52. Разложить данный определитель по элементам: 1) 3-ей строки; 2) 1-го столбца.
1 23
0 1 5
3 2 1
1 1 3
4
2
4
2
53. 1) Разложим данный определитель по элементам 3-ей строки:
A a31 A31 a32 A32 a33 A33 a34 A34a31 1 M 31 a32 1 M 32
4
5
a33 1 M 33 a34 1 M 34
6
7
54.
23 4
1 3 4
4
5
3 1 1 5 2 2 1 0 5 2
1 3 2
1 3 2
1 2 4
1 2
3
6
7
1 1 0 1 2 4 1 0 1 5
1 1 2
1 1 3
3 36 2 2 4 4 11 56
55. 2) Разложим данный определитель по элементам 1-го столбца:
A a11 A11 a21 A21 a31 A31 a41 A41a11 1 M 11 a21 1 M 21
2
3
a31 1 M 31 a41 1 M 41
4
5
56.
1 5 22 3 4
2
3
1 1 2 1 4 0 1 2 1 4
1 3 2
1 3 2
2
3 4
2 3 4
4
5
3 1 1 5 2 1 1 1 5 2
1 3 2
2 1 4
20 0 3 36 32 56
57. Основные методы вычисления определителя
1.разложение определителя по
элементам строки или столбца;
2.
метод эффективного понижения
порядка;
3.
приведение определителя к
треугольному виду.
58.
Метод эффективного пониженияпорядка:
Вычисление
определителя
n-го
порядка сводится к вычислению
одного
определителя
(n-1)-го
порядка, сделав в каком-либо ряду
все
элементы,
кроме
одного,
равными нулю.
59.
1 23
0 1 5
3 2 1
1 1 3
4
2
4
2
×(-3)
×(-1)
1 2
3
4
0 1 5
2
0 4 10 8
0 1 6 2
60.
1 23
4
1 2
0 1 5
2
0 1
2
2 2 1
0 2
5
4
0 2
0 1 6 2
0 1
1 5 1
2
4 1 1 2 5 2 4 14 56
1 6 1
3
5
5
6
2
1
2
1
61. Вычислить определитель приведением его к треугольному виду.
Вычислить определительего к треугольному виду.
1 2
3
0 1 5
3 2 1
1 1 3
4
2
4
2
×(-3)
×(-1)
приведением
1 2
3
4
0 1 5
2
0 4 10 8
0 1 6 2
62.
1 23
4
1 2
0 1 5
2
0 1
2
2 2 1
0 2
5
4
0 2
0 1 6 2
0 1
1 2
0 1
4
0 2
0 1
3
5
5
6
2
1 ×2
2
1
+
3
5
5
6
2
1
2
1
1 2 3 2
0 1 5 1
4
0 0 15 4
0 0 11 2
63.
1 20 1
4
0 0
0 0
2 3
1 5
4 15
2 11
1 2
0 1
4
0 0
0 0
1 2
0 1
4
0 0
0 0
2 3
1 5
4 14 56
2 11
0 7
2 3
1 5
2 11 ×(-2)
4 15
64. Обратная матрица
Матрица A 1 называется обратной к квадратнойматрице A, если A A 1 A 1 A E
A11
1 A21
1
A
A
An1
A12
A22
An 2
T
A1n
A11
A2 n
1 A12
A
Ann
A1n
A21
A22
A2 n
An1
An 2
Ann
Матрица называется вырожденной, если ( A) A 0 ;
в противном случае A – невырожденная матрица.
Теорема. Для того, чтобы матрица имела обратную,
необходимо и достаточно, чтобы она была
невырожденной, т.е. ( A) A 0.
65.
Пример:1
2 3
Найти обратную матрицу для A 2 0 1 .
2 3 1
Имеем:
0 1
a 1 A11
3;
3 1
11
2
2 0
4
2 1
a
1
A
6;
13
a 1 A12
4; 13
2
3
2 1
2 3
a 1 A21
11;
3 1
21
3
a 31
1 A31
4
2 3
2;
0 1
Таким образом:
3
12
a
22
1 3
1 2
5
1 A22
5; a 23 1 A23
7;
2 1
2 3
4
1 3
a 1 A32
7;
2 1
32
5
3
4 6
A 11 5 7 .
2 7 4
1 2
a 1 A33
4.
2 0
33
6
66.
Тогда3 11 2
T
A 4 5 7 .
6 7
4
Вычисляя определитель матрицы A, получаем
|A|=29.
Теперь по формуле:
3
29
1
4
1
T
A
A
29
29
6
29
11
29
5
29
7
29
2
29
7
.
29
4
29
67.
Теорема. Есликвадратные
порядка, то
A и B невырожденные
матрицы
одинакового
( A B) 1 B 1 A 1
68. Ранг матрицы.
a11a21
Рассмотрим матрицу A размера m×n :A ...
a
m1
a12
a22
...
am 2
... a1n
... a2 n
... ...
... amn
Выберем в матрице A произвольно k строк и k столбцов
(k min( m, n)). Элементы, стоящие на пересечении этих
строк и столбцов, составляют матрицу порядка k .
Определитель этой матрицы называется минором k-го
порядка.
Если все миноры k-го порядка равны нулю, то равны
нулю и все миноры более высокого порядка.
Наивысший порядок отличных от нуля миноров
матрицы называется рангом этой матрицы (rangA
или r(A)).
69. Метод вычисления ранга матрицы
1. Привычислении ранга матрицы нужно
переходить от миноров меньших порядков
к минорам больших порядков;
2. Если уже найден минор k-го порядка d
отличный от нуля, то требуют вычисления
лишь
миноры
k+1-го
порядка,
окаймляющие минор d. Если все они равны
нулю, то ранг матрицы равен k.
70. Свойства ранга матрицы
1) Если матрица A имеет размеры m×n, тоrangA min( m, n);
1) rangA 0 тогда и только тогда, когда все элементы
матрицы A равны нулю;
2) если матрица A - квадратная матрица порядка n,
то rangA=n тогда и только тогда, когда
определитель матрицы ( A) 0 .
71.
Обозначим строки (столбцы) матрицы A черезС i , i 1,2,...m.
Строки (столбцы) матрицы C1, C2 ,..., Cm называются
линейно зависимыми, если существуют такие числа
1 , 2 ,..., m , не равные одновременно нулю, что линейная
комбинация строк (столбцов) матрицы равна нулевой
строке:
1C1 2C2 ... mCm ,
где (0,0,...,0).
В противном случае строки матрицы называются
линейно независимыми.
Теорема о ранге матрицы. Ранг матрицы равен
максимальному числу ее линейно независимых строк
(столбцов) (rangA или r(A)).
72.
Элементарные преобразования неменяют ранг матрицы.
Ранг ступенчатой матрицы равен r.














































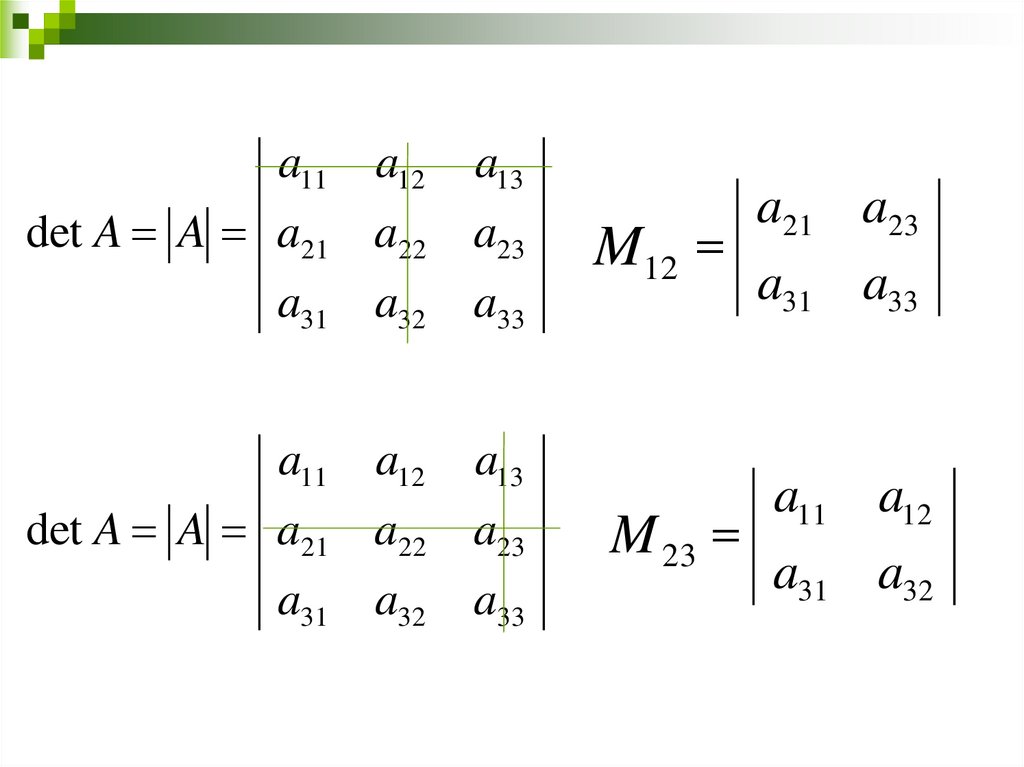


























 mathematics
mathematics








