Similar presentations:
Обратная матрица. Вычисление обратной матрицы
1. Обратная матрица. Вычисление обратной матрицы.
2.
Обра́тная ма́трица — такая матрица A−1, приумножении на которую, исходная матрица A
даёт в результате единичную матрицу E:
Квадратная матрица обратима тогда и только
тогда, когда она невырожденная, то есть её
определитель не равен нулю.
Для неквадратных матриц и вырожденных
матриц обратных матриц не существует.
3. Вычисление обратной матрицы с помощью алгебраических дополнений
4.
5. Нахождение обратной матрицы
Найти матрицу, обратную данной4 5
2
A 3 1 2
4 1 1
1) Находим определитель матрицы
2
4 5
18 0 1
18 1
3 1 2 1 0 3 1 ( 1) 3 2
(18 3 1) 55 0
1 3
4 1 1 4 1 1
Т.о. обратная матрица существует.
2) Составляем союзную матрицу
3 2
1 2
3
2
A12 ( 1)
(3 8) 11
A11 ( 1)
1 2 3
4
1
1 1
A13 ( 1) 4
3 1
3 4 1
4 1
2 4
2 5
4 5
5
4
(2 16) 18
2 20 22 A23 ( 1)
A21 ( 1)
(4 5) 1 A22 ( 1)
4
1
4
1
1 1
3
A31 ( 1) 4
4 5
2 5
2 4
8 5 13 A32 ( 1)5
(4 15) 11 A33 ( 1) 6
2 12 14
1 2
3 2
3 1
3 11 1
*
A 1 22 18
13 11 14
3) Полученную матрицу транспонируем 4) Обратная матрица
1
13
1
13
3
3
1
A*T 11 22
11
A 1 11 22
11
55
1 18 14
1 18 14
6.
7.
8.
9.
10.
11.
12.
Задача 1. Задана квадратная матрица2 3 1
A = 3 4 2
1 1 2
Найти обратную матрицу и сделать проверку.
Задача 2. Задана квадратная матрица
4 3 0
A= 1 1 0
0 0 1
Найти обратную матрицу и сделать проверку.
Задача 3. Задана квадратная матрица
0 0 1
A = 1 5 1
1 4 2
Найти обратную матрицу и сделать проверку.
Задача 4. Задана квадратная матрица
1 2 1
A = 0 3 1
0 2 1
Найти обратную матрицу и сделать проверку.






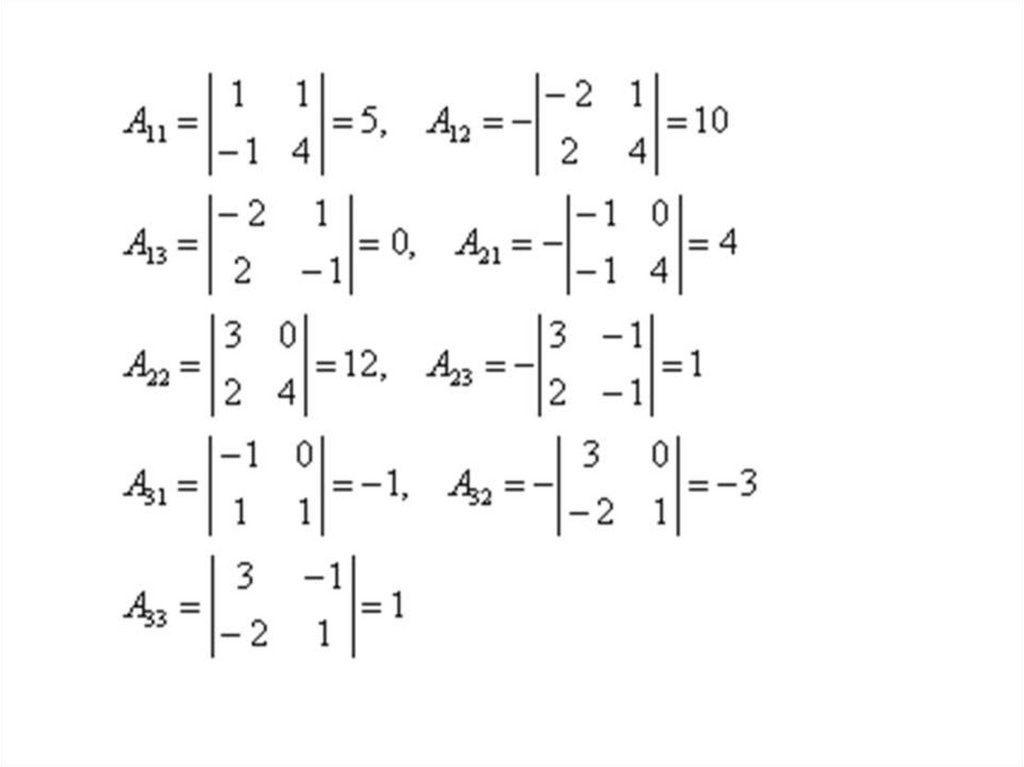





 mathematics
mathematics








