Similar presentations:
Линейная алгебра. Обратная матрица. Вычисление обратной матрицы
1. Линейная алгебра
Обратная матрицаВычисление обратной матрицы
2. Обратная матрица
Обратной матрицей по отношению к данной невырожденнойквадратной матрице A n - ного порядка, называется матрица,
которая, будучи умноженной как слева, так и справа на данную
матрицу, дает единичную матрицу.
Обратная матрица обозначается символом А-1. Таким образом,
согласно определению: АА-1=А-1А=Е.
1
A
A A
A det A 0 A
det A
T
1
Транспонированная матрица
Присоединенная матрица
получается из матрицы А Если определитель матрицы
получается путем замены каждого
путем замены строк т
равен нулю, то обратная
элемента матрицы А на его
соответствующими
матрица не существует
алгебраическое дополнение
столбцами
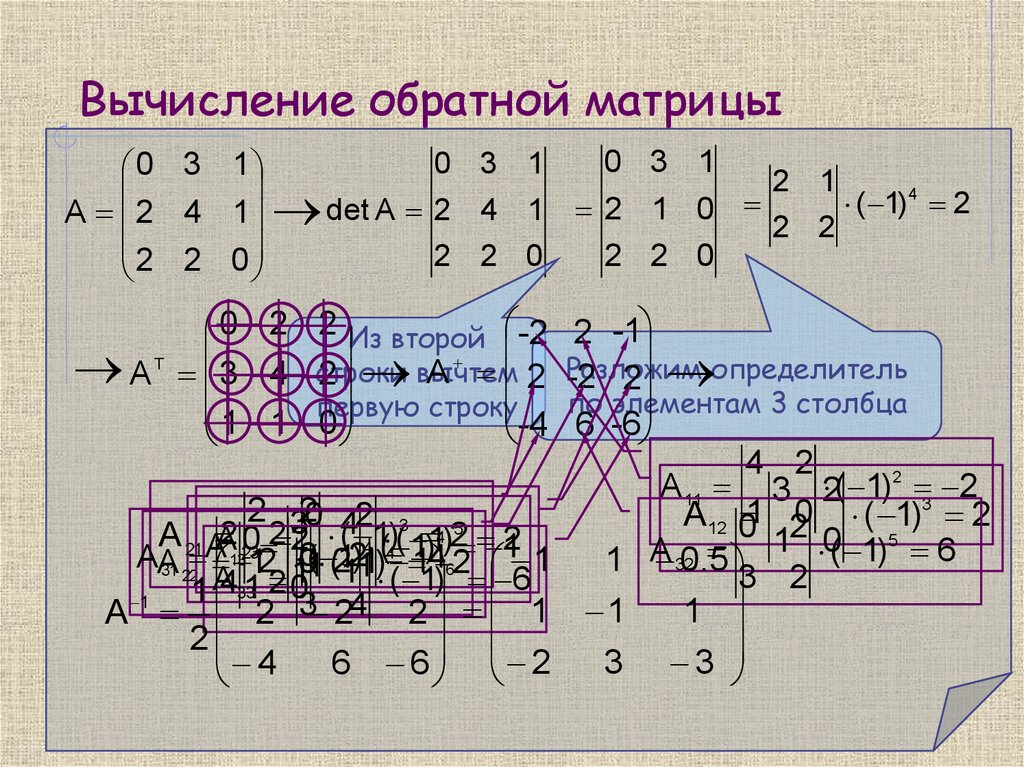
3. Вычисление обратной матрицы
0 3 10 3 1
0 3 1
2 1
4
(
1
)
2
2
1
0
det
A
2
4
1
A 2 4 1
2 2
2 2 0
2 2 0
2 2 0
0 2 2 Из второй -2 2 -1
T
A 3 4 строки
A 2 Разложим
2 вычтем
-2 2 определитель
по элементам
3 столбца
строку
1 1 первую
0
-4 6 -6
4 2
A 11 3 2
( 1)2 3 2
2 320 42 3 5
A 12 0
1 20 ( 1) 2
2 23
2 2 ( 4 1( 4) (
A 21 A
)14)2 1
A
2
0
1 0( 1)5 6
1
A
13
0
2
AA
(
1
)
4
1 320.5 3 2
12 101 (21 11) ( 11 ) 62 6 1
31 22
A
1 4331 2 03 4
1
1
A 2 2
2 1 1
2
2
3
3
4
6
6


 mathematics
mathematics








