Similar presentations:
Основные законы распределения непрерывных случайных величин
1.
Основные законыраспределения непрерывных
случайных величин
2. Равномерное распределение
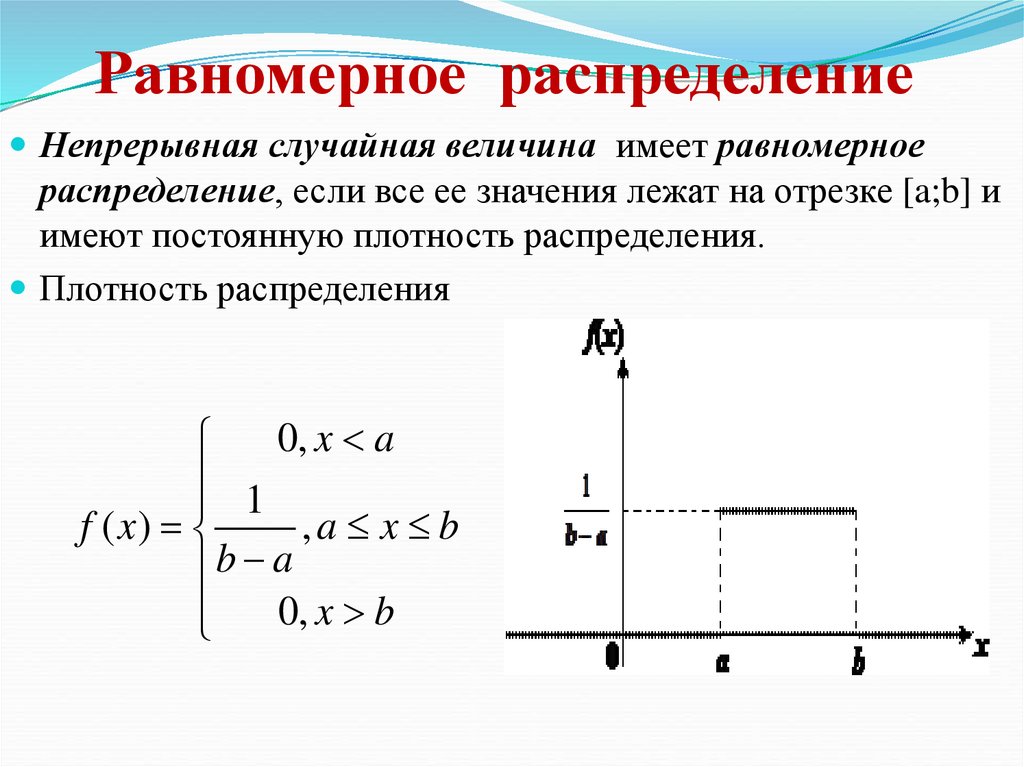
Непрерывная случайная величина имеет равномерноераспределение, если все ее значения лежат на отрезке [a;b] и
имеют постоянную плотность распределения.
Плотность распределения
0, x a
1
f ( x)
,a x b
b a
0, x b
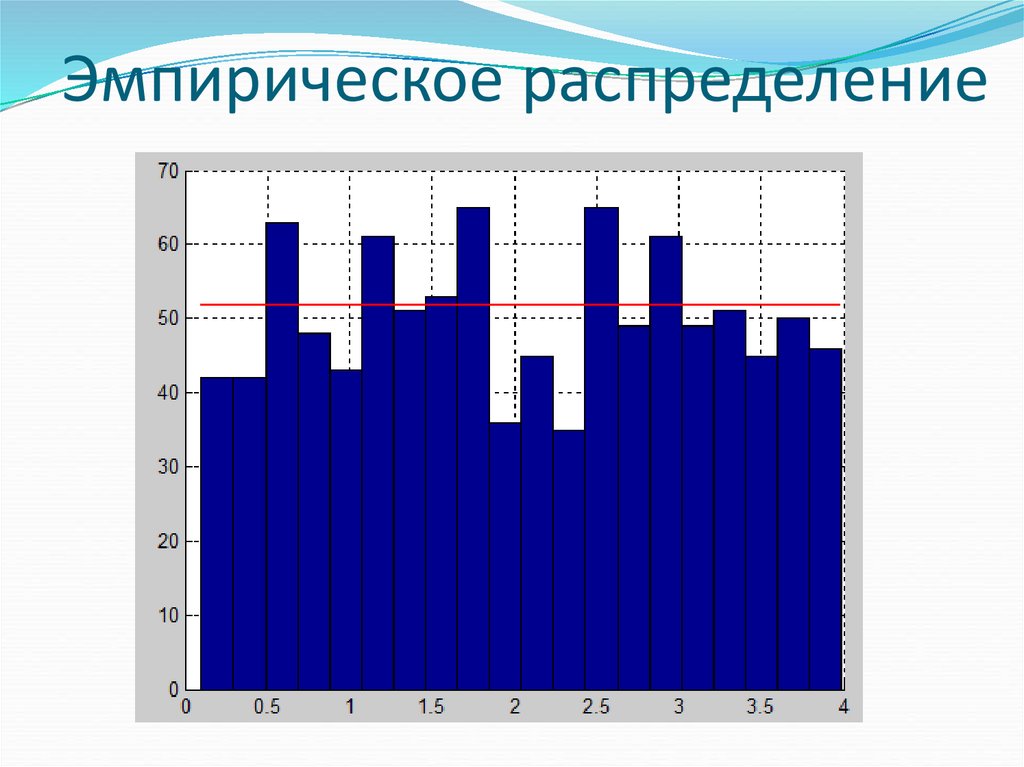
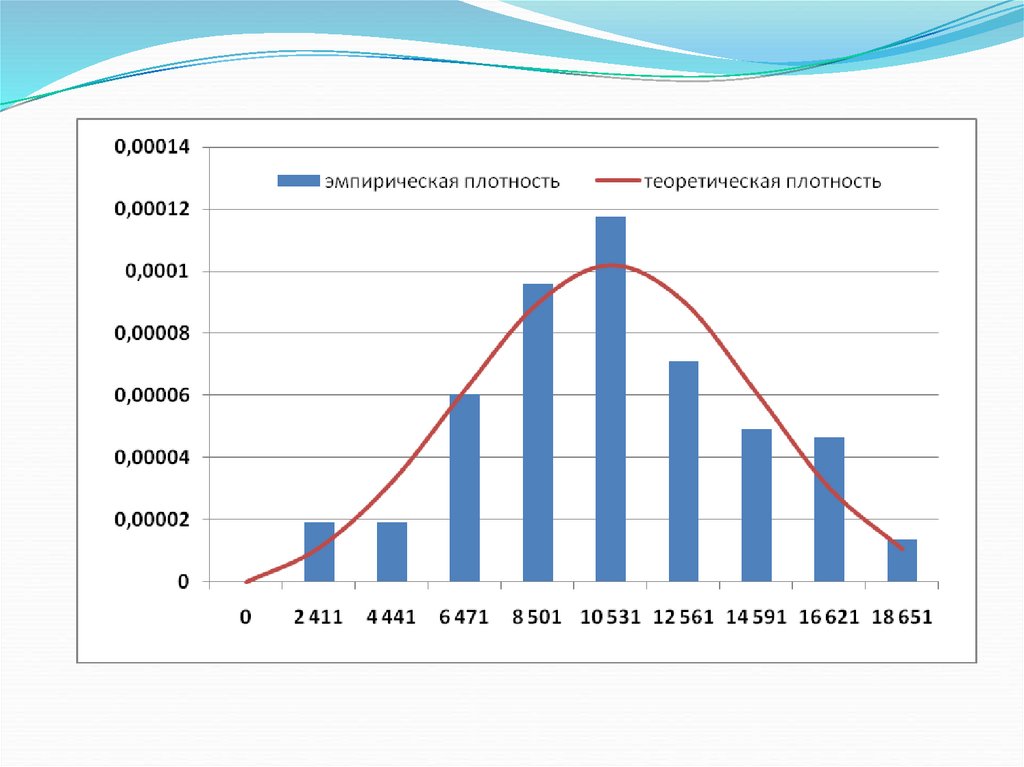
3. Эмпирическое распределение
4. Равномерное распределение
К случайным величинам, имеющими равномерноераспределение, относятся:
время ожидания пассажиром транспорта, курсирующего с
постоянным интервалом;
ошибки округления числа до целого, которая равномерно
распределена на отрезке [– 0,5; 0,5];
случайные величины, все значения которых принадлежат
некоторому интервалу и все эти значения имеют одинаковую
вероятность;
ошибки при измерениях.
5. Равномерное распределение
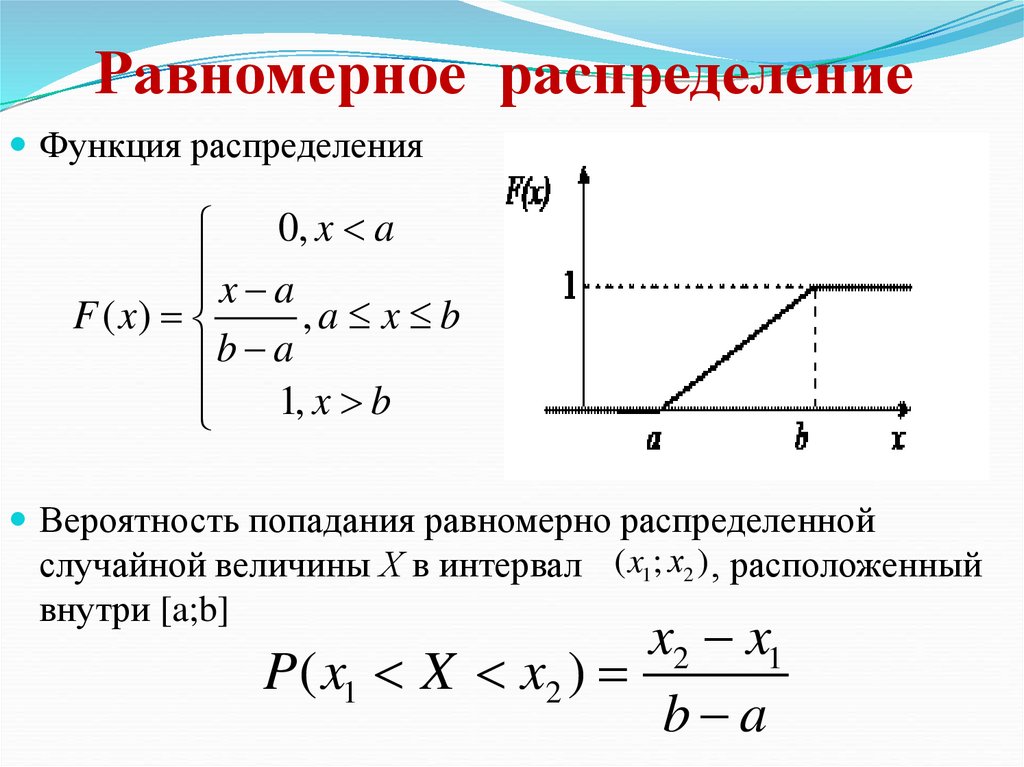
Функция распределения0, x a
x a
F ( x)
,a x b
b a
1, x b
Вероятность попадания равномерно распределенной
случайной величины Х в интервал ( x1; х2 ) , расположенный
внутри [a;b]
x2 x1
P( x1 X x2 )
b a
6. Характеристики равномерного распределения
Математическое ожиданиеa b
M (X )
2
Математическое ожидание равномерно распределенной на
отрезке [a,b] случайной величины Х равно абсциссе
середины отрезка.
Дисперсия
2
(b a)
D( X )
12
Среднее квадратическое отклонение
b a
(X )
2 3
7.
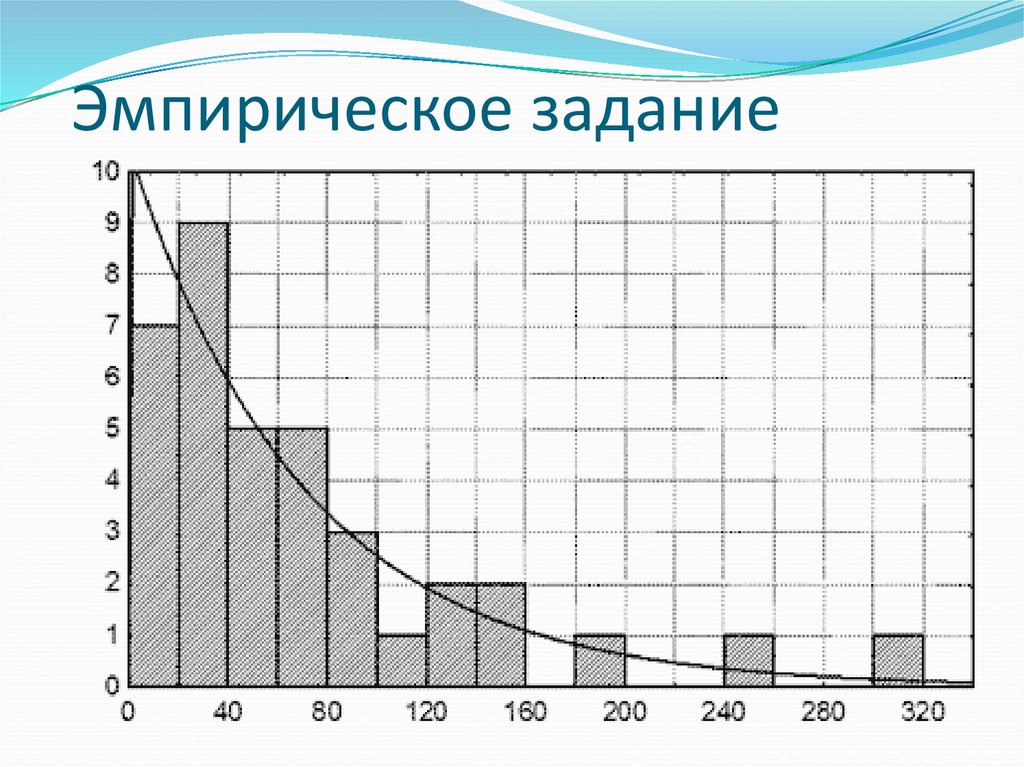
Пример 18. Показательное распределение
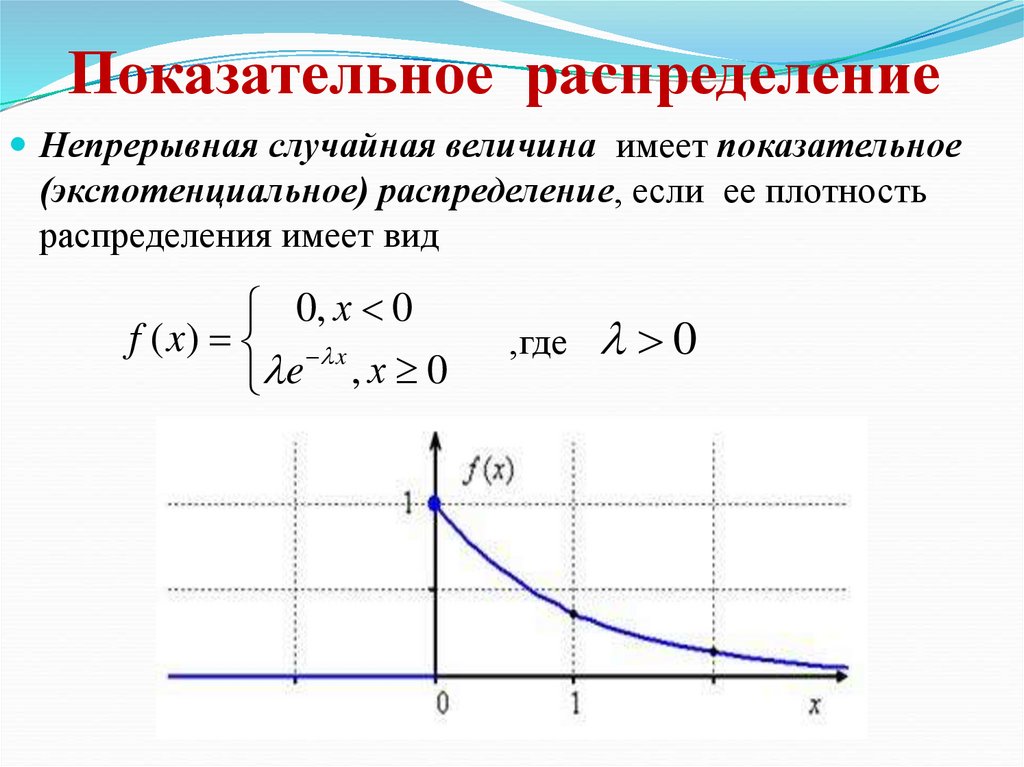
Непрерывная случайная величина имеет показательное(экспотенциальное) распределение, если ее плотность
распределения имеет вид
0, х 0
f ( x) x
e , х 0
,где
0
9. Эмпирическое задание
10. Показательное распределение
Показательное распределение используется— при моделировании производства
— при моделировании систем массового обслуживания
— в теории расписаний (очередей) для моделирования
промежутков времени между двумя запросами, которые
могут представлять собой приход клиента в банк (ресторан),
поступление пациента в больницу, а также посещение Webсайта.
Распределение зависит только от одного параметра λ и
представляет собой среднее количество запросов,
поступающих в систему за единицу времени.
Величина 1/λ равна среднему промежутку времени,
прошедшего между двумя последовательными запросами.
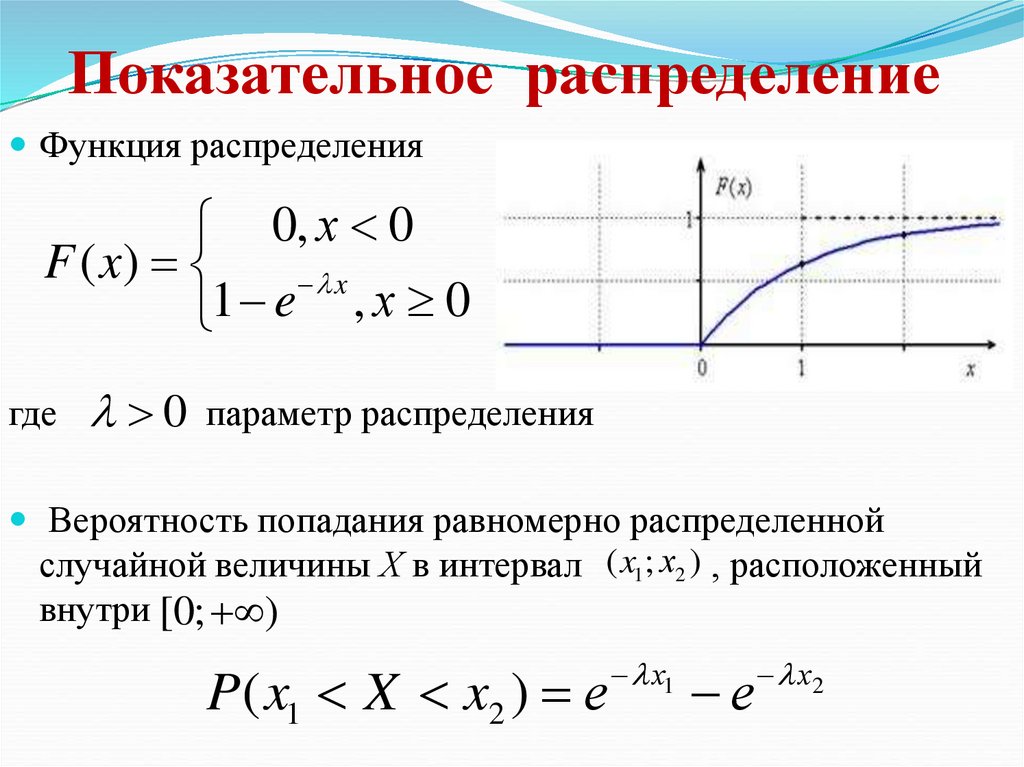
11. Показательное распределение
Функция распределения0, х 0
F ( x)
x
1 e , х 0
где
0 параметр распределения
Вероятность попадания равномерно распределенной
случайной величины Х в интервал ( x1; х2 ) , расположенный
внутри [0; )
P( x1 X x2 ) е
х1
е
х2
12. Характеристики показательного распределения
Математическое ожиданиеM (X )
Дисперсия
D( X )
1
1
2
Среднее квадратическое отклонение
(X )
1
13.
Пример 214. Нормальное распределение
Непрерывная случайная величина ξ имеетнормальное распределение с параметрами a и σ,
если плотность распределения имеет вид
1
f ( x)
e
2
( x a )2
2 2
~ N ( a, )
Вероятностный смысл параметров:
a M ( ) , D( )
15.
16.
Нормальное распределениезакон проявляется во всех случаях, когда случайная
величина является результатом действия большого числа
различных факторов. К нормальному закону
приближаются все остальные законы распределения.
Нормальное распределение часто встречается в природе.
Например, следующие случайные величины хорошо
моделируются нормальным распределением:
отклонение при стрельбе;
погрешности измерений (однако погрешности некоторых
измерительных приборов имеют иное распределение);
некоторые характеристики живых организмов в
популяции.
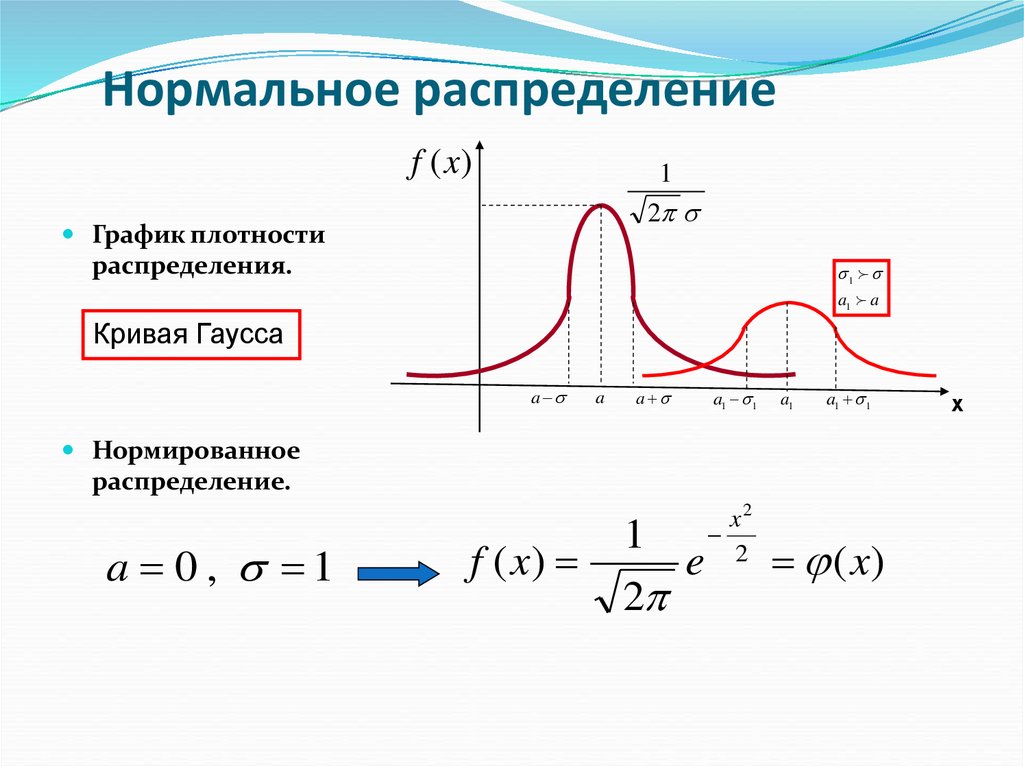
17. Нормальное распределение
f (x )1
2
График плотности
распределения.
1
a1 a
Кривая Гаусса
a
a
a
a1 1
a1
a1 1
Нормированное
распределение.
a 0 , 1
f ( x)
1
e
2
x2
2
( x)
х
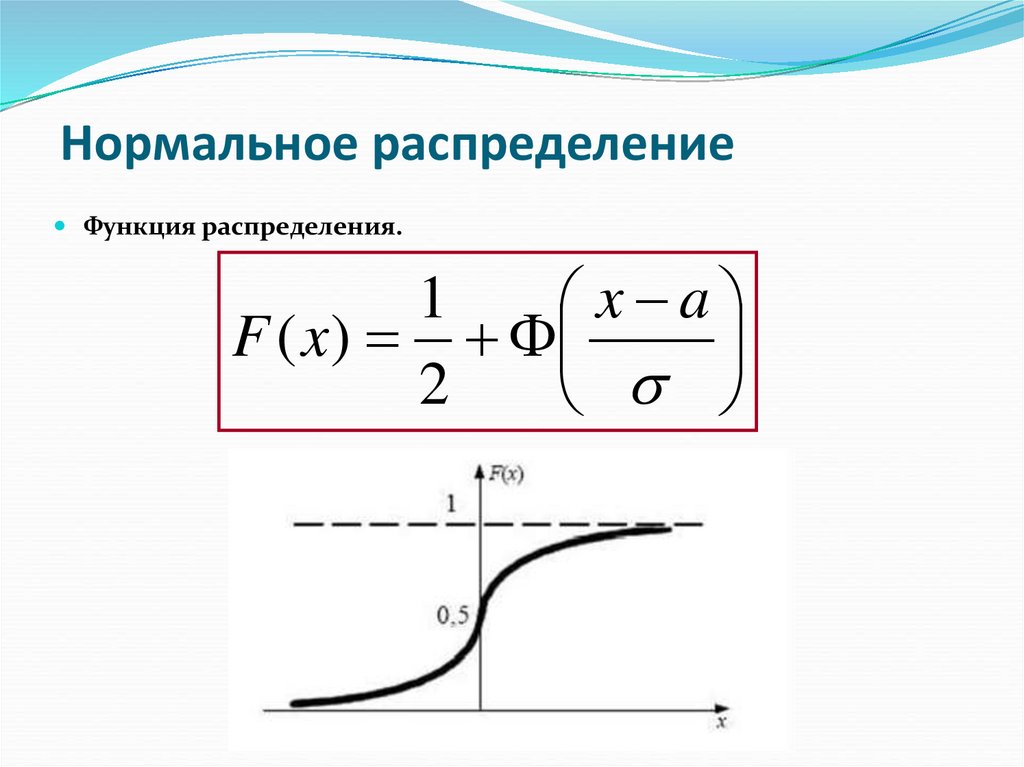
18. Нормальное распределение
Функция распределения.1
x a
F ( x)
2
19. Нормальное распределение
Вероятность попадания в интервал.x2 a
x1 a
P ( x1 x2 )
Следствие
вероятность отклонения ξ от а не более чем на ε)
P( a ) 2
20. Нормальное распределение
Правило «3σ».3
P( a 3 ) 2
2 (3) 0,9973
Практически достоверно, что
N (a, ) [a 3 , a 3 ]
21.
Пример 322.
Пример 423.
Пример 5Предприятие изготавливает трубы, средний внешний диаметр которых
равен 20,2 мм, а стандартное отклонение равно 0,25 мм. Внешний
диаметр не должен превышать определенное значение (предполагается,
что нижняя граница не важна). Какую верхнюю границу в технических
условиях необходимо установить, чтобы ей соответствовало 97,5% всех
изготавливаемых изделий?
Решение
a 20,20 мм, 0,25 мм
p
p x a 2
2
0.975
0.4875
2
По ттаблиц Ф(х) определяем , что если Ф( x) 0,4875, то x 2,24
2,24 2,24 0,56
Верхняя граница определяет ся соотношением
a 20,20 0,56 20,76 мм














 mathematics
mathematics








