Математическое ожидание случайной величины. Совместное распределение двух случайных величин (Урок 24)

1. Математическое ожидание случайной величины. Совместное распределение двух случайных величин

МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ.
СОВМЕСТНОЕ РАСПРЕДЕЛЕНИЕ
ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
УРОК 24

2.

• ПРОВЕРОЧНАЯ РАБОТА
2

3.

Распределение вероятностей
Закон распределения вероятностей
• Что является важной характеристикой случайной величины?
множество её возможных значений
• Из чего состоит множество значений дискретной случайной величины?
оно состоит из множества отдельно отстоящих друг от
друга, чаще всего целых, чисел
3

4.

Пример 1. Подбрасывают два игральных кубика. Пусть:
X — число, выпавшее на первом кубике;
Y — число, выпавшее на втором кубике;
S — сумма чисел, выпавших на кубиках;
W — наибольшее из чисел, выпавших на кубиках;
V — наименьшее из чисел, выпавших на кубиках.
Вычислите вероятность, с которой величины X и Y принимают все свои
значения Величины X и Y принимают все свои значения с одинаковой
вероятностью 1/6 .
Почему для величины W значение 6 явно вероятнее, чем 1?
Наибольшее из чисел будет равно шести для одиннадцати
исходов этого опыта (перечислите их), а единице — только для
одного. 61 62 63 64 65 66 16 26 36 46 56 – для 6
11 – для 1 .
4

5.

Пример 1. Подбрасывают два игральных кубика. Пусть:
X — число, выпавшее на первом кубике;
Y — число, выпавшее на втором кубике;
S — сумма чисел, выпавших на кубиках;
W — наибольшее из чисел, выпавших на кубиках;
V — наименьшее из чисел, выпавших на кубиках.
Почему для величины V значение 1 явно вероятнее, чем 6?
Для величины V значение 1 явно вероятнее, чем 6: ведь
наименьшее из чисел будет равно 1 для одиннадцати исходов этого
опыта , а 6 — только для одного.
5

6.

Таким образом, важно знать не только возможные значения случайной
величины, но и вероятности этих значений. Эта информация называется
распределением вероятностей случайной величины или законом
распределения, распределением случайной величины
Распределением вероятностей случайной величины называется
закон, который описывает все возможные значения случайной
величины, а также вероятности, с которыми она их принимает.
Название «распределение вероятностей» объясняется тем, что этот закон показывает, как вся вероятность, равная 1,
распределена между отдельными значениями случайной величины.
Для дискретных величин с небольшим количеством значений самым удобным способом представления такого закона
служит таблица, состоящая из двух строк: в первой строке указываются по возрастанию все возможные значения, а во
второй — их вероятности.
6

7.

Если случайная величина X принимает значения x1 , x2 , … , xn
с вероятностями p1 , p2 , … , pn , то её закон распределения будет выглядеть
так
7

8.

Пример 1. Подбрасывают два игральных кубика. Пусть:
X — число, выпавшее на первом кубике;
Y — число, выпавшее на втором кубике;
Заполните таблицу распределения величин X и Y
8

9.

Пример 1. Подбрасывают два игральных кубика. Пусть:
S — сумма чисел, выпавших на кубиках;
Чтобы найти закон распределения случайной величины S и любой другой
величины, связанной с этим опытом, удобно сначала заполнить таблицу, в
которой будут перечислены все 36 возможных исходов этого опыта и для
каждого исхода указано значение интересующей нас величины. Заполните
таблицу для случайной величины S.
Из таблицы хорошо видно, сколько раз
встречалось каждое значение суммы:
например, сумма 5 встречалась 4 раза, а
сумма 7 — 6 раз. Остаётся построить по
этим данным закон распределения для
случайной величины S.
9

10.

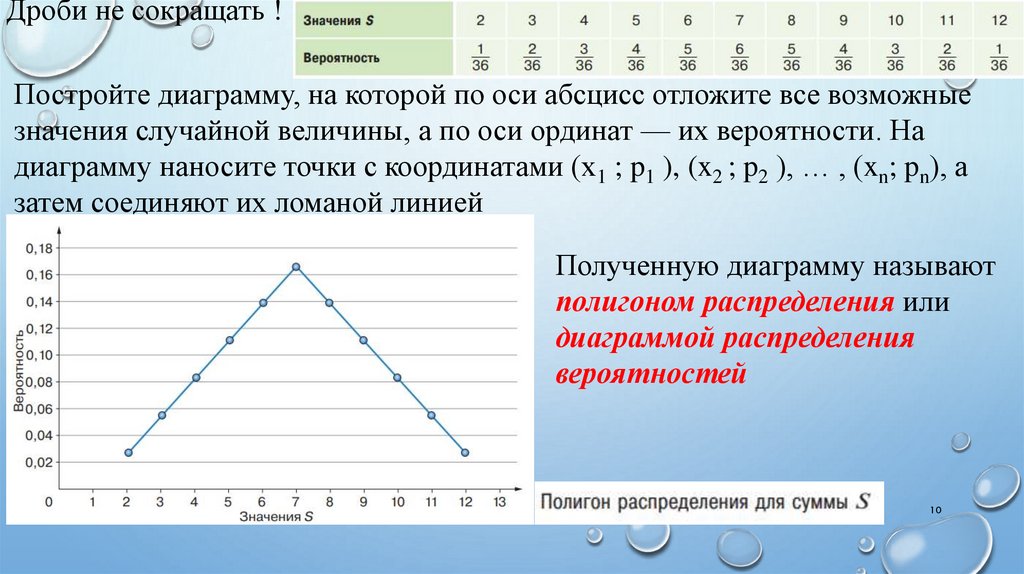
Дроби не сокращать !
Постройте диаграмму, на которой по оси абсцисс отложите все возможные
значения случайной величины, а по оси ординат — их вероятности. На
диаграмму наносите точки с координатами (x1 ; p1 ), (x2 ; p2 ), … , (xn; pn), а
затем соединяют их ломаной линией
Полученную диаграмму называют
полигоном распределения или
диаграммой распределения
вероятностей
10

11.

Найдём закон распределения бинарной случайной величины I,
которая является индикатором некоторого случайного события A.
Напомним, что она равна 1, если событие A происходит, и равна 0,
если не происходит. Если P(A) = p, то закон распределения I
выглядит так
Законы распределения дискретных случайных величин могут быть самые разные.
Но в любом из них всегда выполняется важное свойство: сумма всех вероятностей в любом законе
распределения всегда равна 1: p1 + p2 + … + pn = 1. Если оно не выполнено, значит, либо в таблицу попали не все
возможные значения случайной величины, либо произошла ошибка при вычислении какой-то из вероятностей.
Можете убедиться, что во всех найденных нами законах это свойство выполнено. В каких-то задачах проверка этого
свойства позволит вам найти ошибку в найденном распределении, а в каких-то — избавит от вычисления последней
(иногда самой трудной) вероятности. Её можно будет найти, вычитая сумму всех остальных вероятностей из 1
11