Similar presentations:
Математическое ожидание суммы случайных величин
1. Математическое ожидание суммы случайных величин
2. Повторение.
Пусть распределение вероятностей случайной величиныХ задано таблицей
Математическим ожиданием дискретной
случайной величины называется сумма
произведений ее возможных значений на
соответствующие им вероятности.
Е(Х)= х1 • p1 + х2 • p2 + х3 • p3 + … + хn • pn
3. № 1
№1Дискретная случайная величина X принимает три
возможных значения: x1=4 с вероятностью p1=0,5; x2=6 c
вероятностью p2=0,3 и x3 с вероятностью p3. Найти x3 и
p3, зная, что Е(X)=8.
4. Математическое ожидание суммы случайных величин
Математическое ожидание суммы случайныхвеличин равно сумме математических
ожиданий слагаемых:
5. № 2
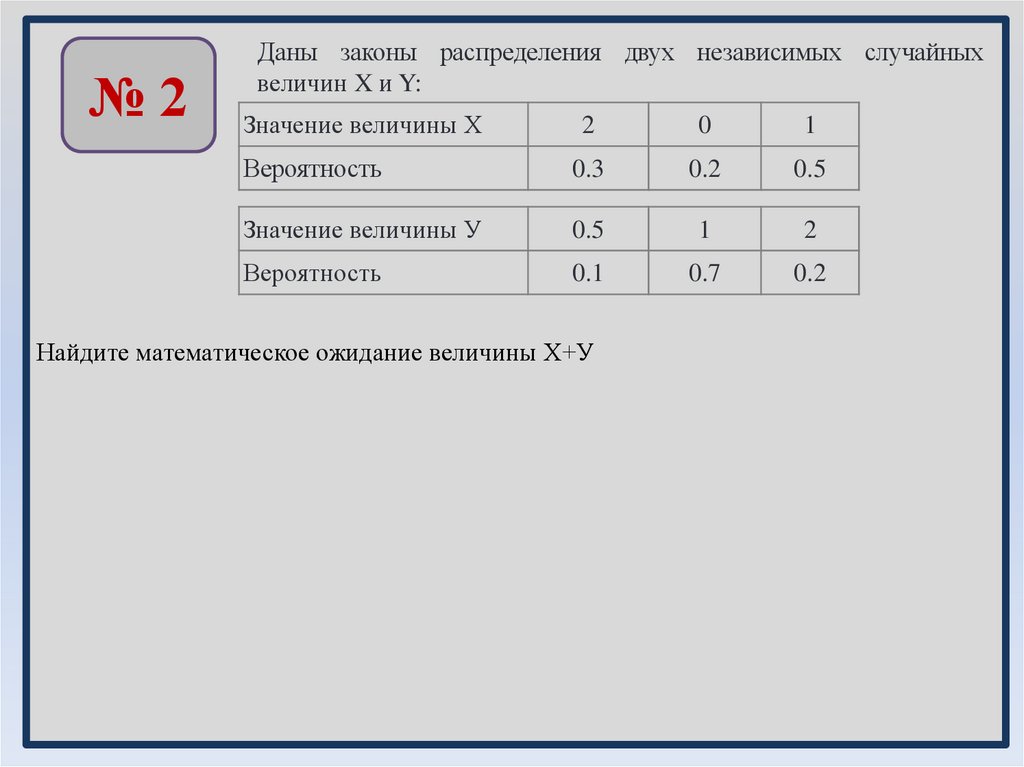
№2Даны законы распределения двух независимых случайных
величин X и Y:
Значение величины Х
2
0
1
Вероятность
0.3
0.2
0.5
Значение величины У
0.5
1
2
Вероятность
0.1
0.7
0.2
Найдите математическое ожидание величины Х+У
6. № 3
№37. № 4
№4Производится 3 выстрела с вероятностями попадания в цель,
равными p1=0,4; p2=0,3 и p3=0,6. Найти математическое
ожидание общего числа попаданий.
8. № 5
№5Даны законы распределения трёх независимых случайных величин X, Y, Z
-5
Значение
величины Х
-7
-8
1
-1
-2
4
2
1
Вероятность 0.03
0.21
0.06
0.02
0.14
0.04
0.05
0.35
0.1
Значение
величины Y
-8
-7
-5
-2
-1
1
2
4
Вероятность
0.06
0.21
0.03
0.04
0.14
0.12
0.35
0.05
Значение
величины Z
-1
0
1
Вероятность
0.03
0.12
0.15
Найдите математическое ожидание величины Х+У+ Z
9. № 6
№6Найти математическое ожидание суммы числа очков, которые
могут выпасть при бросании двух игральных костей.









 mathematics
mathematics








