Similar presentations:
Операции над случайными величинами. Урок 13
1. Операции над случайными величинами
Урок 132011
Работу выполнила
студентка группы ПОВ 54
Исакова Ольга
2. Случайные величины
Случайной называется величина, которая в результате опытаможет принять то или иное возможное значение, неизвестное
заранее, но обязательно одно. (с.в. X, Y, Z; знач. с.в. x, y, z)
Примеры случайных величин
Число мальчиков, родившихся в течение суток в
определенном городе.
Значение
температуры
измерении.
Число выпавших
бросании монеты.
“гербов”
при
пятикратном
При однократном
выпавших очков
бросании
кости
количество
при
неоднократном
3. Различают случайные величины следующих типов:
Случайные величиныРазличают случайные величины следующих типов:
Дискретные и непрерывные
Дискретной случайной величиной называют
такую случайную величину, множество возможных
значений
которой
либо
конечное,
либо
бесконечное, но счетное.
Непрерывной случайной величиной называют
такую случайную величину, которая может принять
любое значение из некоторого конечного или
бесконечного интервала.
4. Закон распределения случайной величины
Закономраспределения
случайной
величины
называется правило, устанавливающее связь между
возможными значениями случайной величины и
соответствующими им вероятностями.
Закон распределения может быть представлен в
•Табличном
•Аналитическом
•Графическом виде
5. Дискретные случайные величины
Простешей формой задания закона дискретнойслучайной величины является таблица, в которой
перечислены возможные значения случайных величин
(упорядоченные по возрастающей) и соответствующие
им вероятности.
X
x1
x2
…
xn
P(X)
p1
p2
…
pn
6. Дискретные случайные величины
Пусть случайная величина X может принять одно из nвозможных значений x1,…, xn, с вероятностью p1,…, pn
соответственно.
Тогда закон распределения случайной величины X можно
записать в виде таблицы
X
x1
x2
…
xn
P(X)
p1
p2
…
pn
где х1<х2<…<хn.
n
pi 1
i 1
7. Произведением kX
Произведением kX случайной величины Х на постояннуювеличину k называется новая случайная величина Z=kX,
которая с теми же вероятностями, что и Х, принимает
значения, равные произведениям значений случайной
величины Х на k, т.е. =kxi.
X
x1
x2
…
xn
P(X)
p1
p2
…
pn
Z=kX
kx1
kx2
…
kxn
P(X)
p1
p2
…
pn
8. Квадрат случайной величины
Квадратом случайной величины Х, т.е. Х2, называетсяновая случайная величина Z=X2, которая с теми же
вероятностями, что и Х, принимает значения, равные
квадратам значений случайной величины Х, т.е. zi=xi2.
X
x1
x2
…
xn
P(X)
p1
p2
…
pn
Z
(x1)2
(х2)2
…
(хn)2
P(X)
p1
p2
…
pn
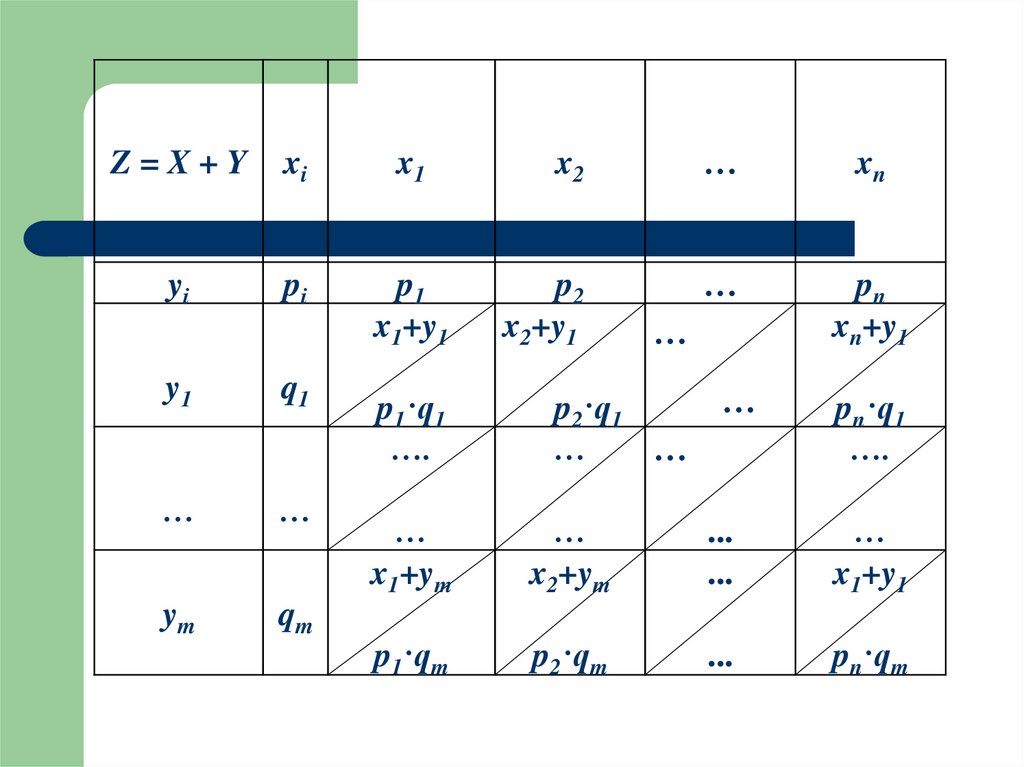
9. Сумма
Суммой случайных величин X и Y называется новаяслучайная величина Z=X+Y, которая принимает все
значения вида
zij = xi + yj (i = 1,2,..n; j = 1,2,...,m)
с вероятностями pij,
причем pij = P(X = xi; Y = yj) = P(X = xi) · PX = xi(Y = yj).
Если случайные величины X и Y независимые, то
pij = pi · qj.
10.
Решение:Значение случайной величины Z найдем, если сложим
каждое значение случайной величины X с каждым
значением случайной величины Y. Соответствующие
вероятности складываемых значений xi и yi будем
перемножать.
Для записи решения составим таблицу.
11.
Z=X+Yxi
x1
x2
…
xn
yi
pi
p1
x1+y1
p2
x2+y1
…
…
pn
xn+y1
p1·q1
….
…
p2·q1
…
…
pn·q1
….
…
x1+ym
…
x2+ym
...
...
…
x1+y1
p1·qm
p2·qm
...
pn·qm
y1
q1
…
…
ym
qm
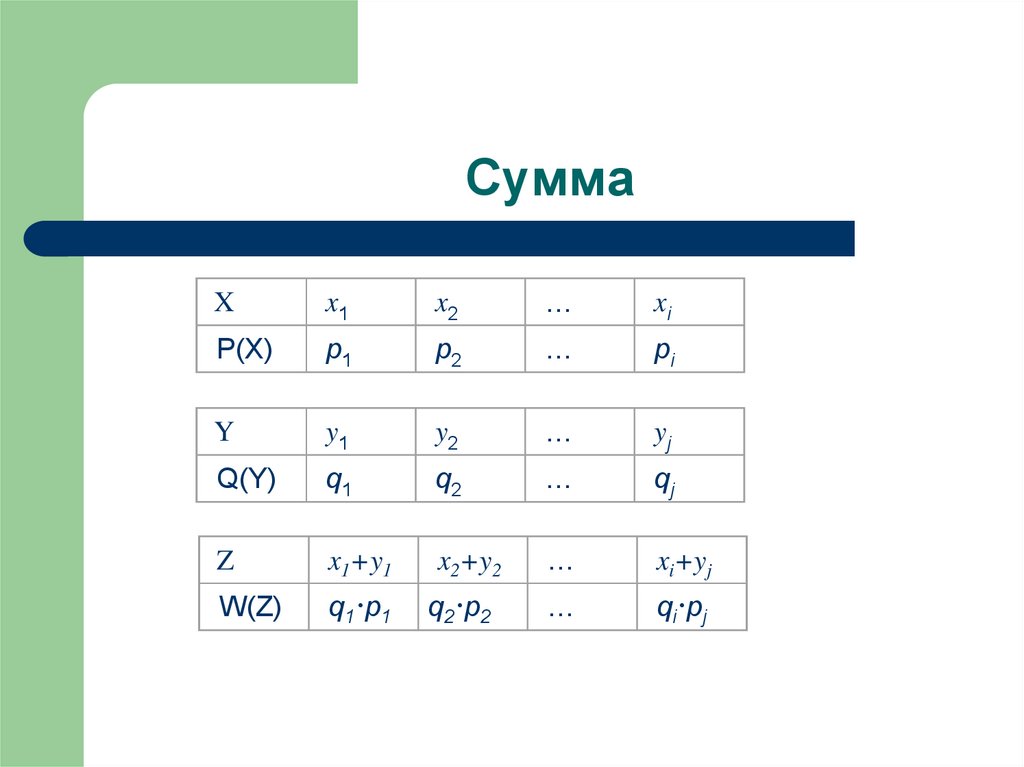
12. Сумма
Xx1
x2
…
xi
P(X)
p1
p2
…
pi
Y
y1
y2
…
yj
Q(Y)
q1
q2
…
qj
Z
x1+y1
x2+y2
…
xi+yj
W(Z)
q1·p1
q2·p2
…
qi·pj
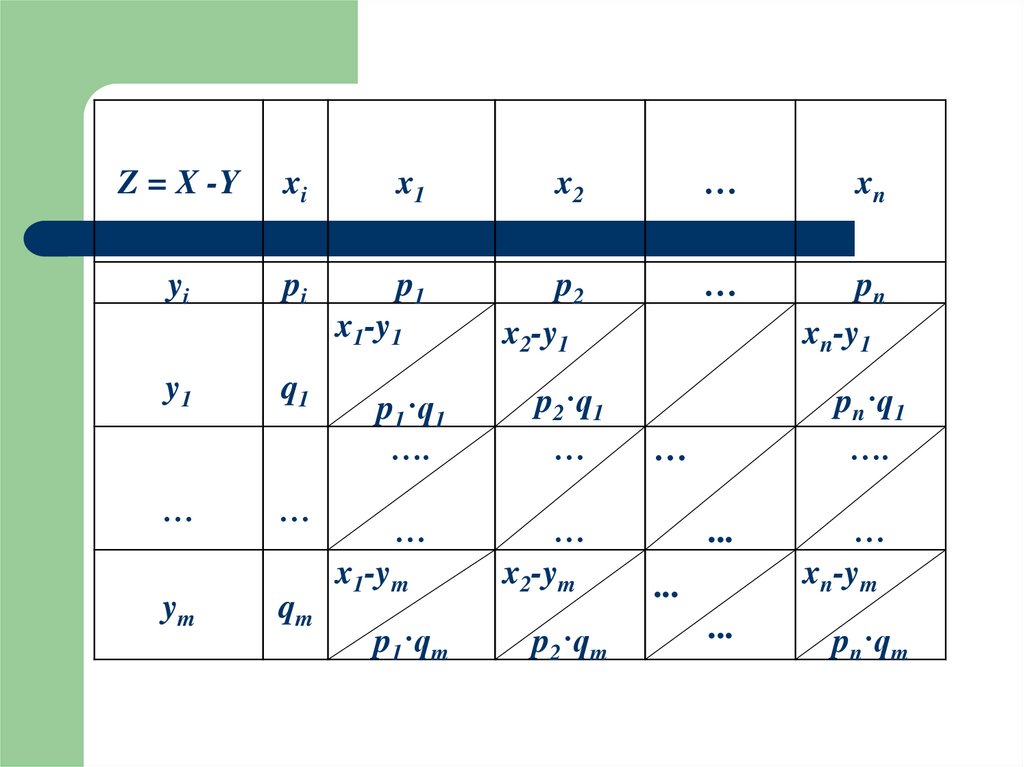
13. Разность
Разностью случайных величин X и Y называетсяновая случайная величина
Z = X - Y, которая принимает все значения вида
zij = xi - yj с вероятностями pij,
причем pij = P(X = xi; Y = yj) = P(X = xi)·PX=xi(Y = yj).
Если случайные величины X и Y независимые, то
pij = pi · qj.
14.
Решение:Значение случайной величины Z найдем, если вычтем из
каждого значения случайной величины X каждое значение
случайной величины Y. Соответствующие вероятности
вычитаемых значений xi и yi будем перемножать.
Для записи решения составим таблицу.
Для записи решения составим таблицу.
15.
Z = X -Yxi
x1
x2
…
xn
yi
pi
p1
p2
x2-y1
…
pn
xn-y1
x1-y1
y1
…
ym
q1
…
qm
p1·q1
….
p2·q1
…
…
…
x2-ym
x1-ym
p1·qm
p2·qm
pn·q1
….
…
...
…
xn-ym
...
pn·qm
...
16. Разность
Xx1
x2
…
xi
P(X)
p1
p2
…
pi
Y
y1
y2
…
yj
Q(Y)
q1
q2
…
qj
Z
x1-y1
x2-y2
…
xi-yj
W(Z)
q1·p1
q2·p2
…
qi·pj
17. Разность
Zz1
z2
…
zi
p(Z)
pz1
pz2
…
pzj
18. Вычтем из каждого значения Х каждое значение У:
z11 = x1 – y1z12 = x1 – y2
z1m = x1 – ym
…
z21 = x2 – y1
z22 = x2 – y2
z2m = x2 – ym
…
19. Вычтем из каждого значения Х каждое значение У:
z31 = x3 – y1z32 = x3 – y2
z3m = x3 – ym
…
zn1 = xn – y1
zn2 = xn – y2
znm = xn – ym
20. Найдем вероятности вычисленных значений:
P(X = х1) ∙ P(Y = у1)P(Z = z12) = P(X = х1) ∙ P(Y = у2)
P(Z = z1m) = P(X = х1) ∙ P(Y = уm)
......
P(Z = z11) =
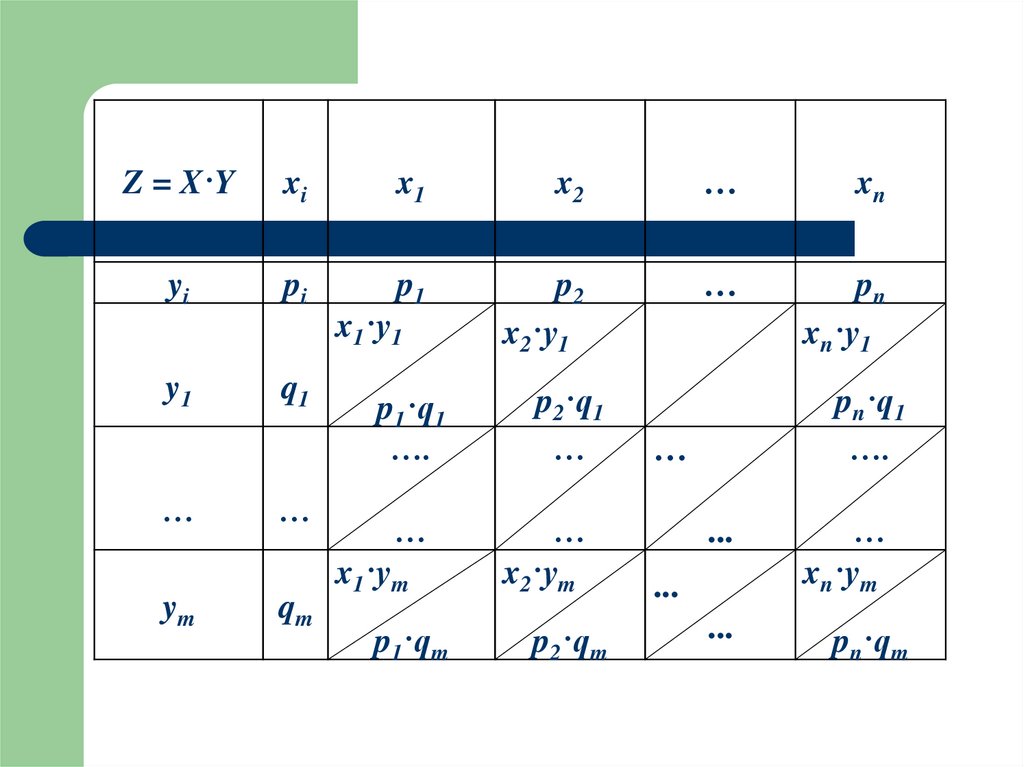
21. Произведение
Произведением случайных величин X и Yназывается новая случайная величина
Z = XY, которая принимает все значения вида
zij = xiyj, с вероятностями pij,
причем pij = P(X = xi; Y = yj) = P(X = xi) · PX = xi(Y = yj).
22.
Решение:Значение величины Z найдем, если умножается
каждое значение случайной величины X с каждым
значением случайной величины Y. Соответствующие
вероятности умножаемых значений xi и yi будем
перемножать.
Для записи решения составим таблицу.
23.
Z = X·Yxi
x1
x2
…
xn
yi
pi
p1
p2
x2·y1
…
pn
xn·y1
y1
q1
p1·q1
….
p2·q1
…
…
…
x2·ym
…
ym
…
qm
x1·y1
x1·ym
p1·qm
p2·qm
pn·q1
….
…
...
…
xn·ym
...
pn·qm
...
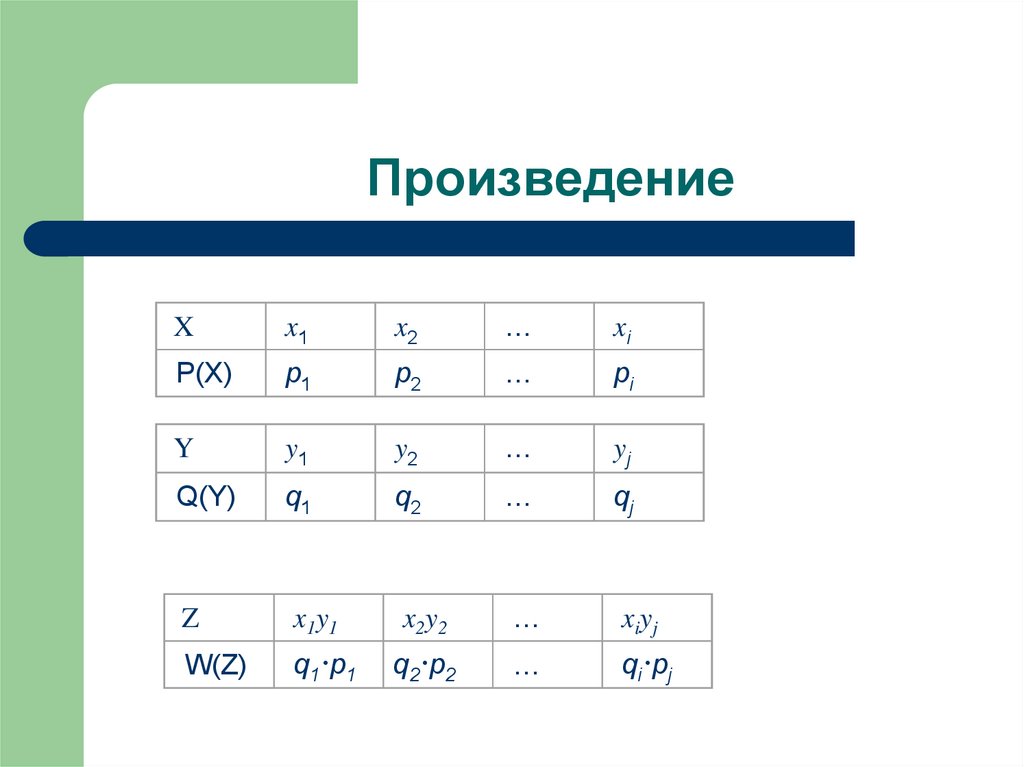
24. Произведение
Xx1
x2
…
xi
P(X)
p1
p2
…
pi
Y
y1
y2
…
yj
Q(Y)
q1
q2
…
qj
Z
x1y1
x2y2
…
xiyj
W(Z)
q1·p1
q2·p2
…
qi·pj
25. Вопросы
Что называется случайной величиной?Какие типы случайной величины вы знаете?
Дайте определение дискретной случайной
величины.
Дайте определение непрерывной случайной
величины.





















 mathematics
mathematics








