Решение задач части С по планиметрии

1.

Муниципальное образовательное учреждение основная
общеобразовательная школа №7 г.о. Тольятти
Решение задач части С
(планиметрия).
учитель математики высшей категории
Холова Сания Минзакировна

2.

Данная тема актуальна, так как подобные задачи требуют
развитого абстрактного мышления. Задачи С4 предполагают
выполнение действий с геометрическими фигурами. Наглядное
решение позволяет лучше усвоить приемы решения таких
задач. Их особенностью является рассмотрение различных
конфигураций геометрических фигур. Задачи, представленные
ниже, очень часто вызывают у учащихся затруднения при
решении. Чтобы решить их, нужно хорошо знать планиметрию.
А так как изучение планиметрии заканчивается в 9 классе, то на
уроках геометрии в 10 – 11 классах необходимо решать задачи
повышенной сложности из планиметрии.

3.

Задача 1
Прямоугольный треугольник разделен на два
треугольника. Перпендикуляром, опущенным из
вершины прямого угла на гипотенузу. В
образовавшиеся треугольники вписаны
окружности с радиусами r1 5иr2 12.
Найдите радиус окружности, вписанной в данный
треугольник.

4. Решение

В
А
С
D
Обозначим радиусы окружностей, вписанных в
треугольники АВD и ВСD , r1 и r2
соответственно ( r1 = 5, r2 = 12 – по условию)

5.

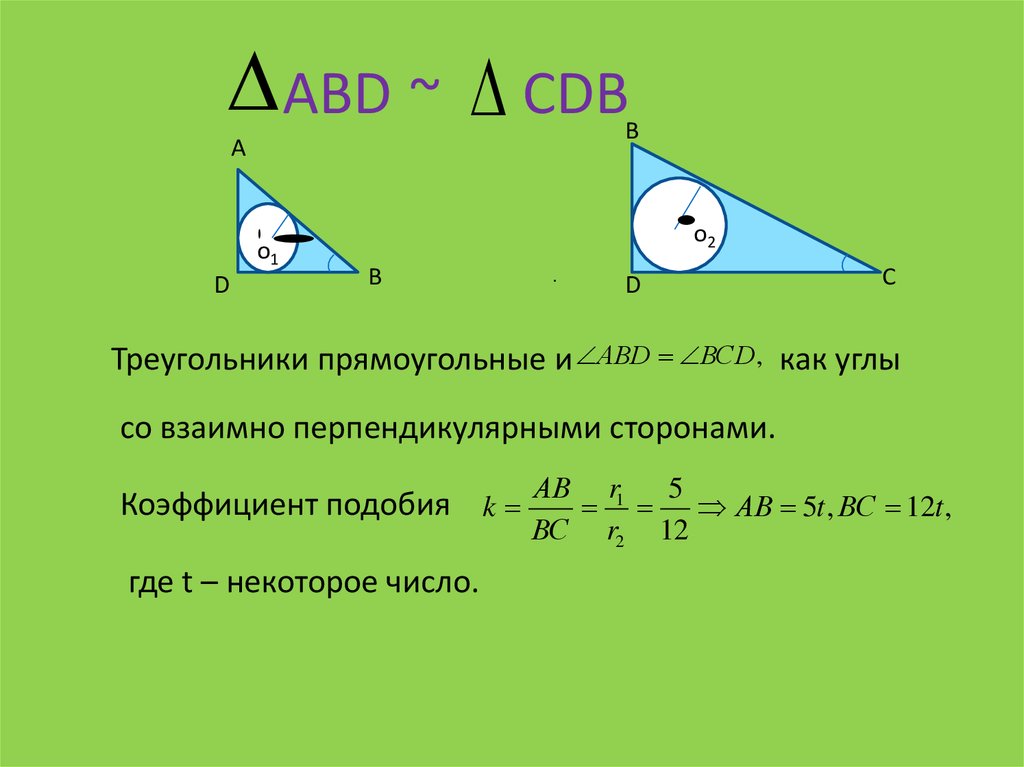
АВD ~ СDВ
В
А
о1
D
о
2
В
D
С
Треугольники прямоугольные и АВD ВСD , как углы
со взаимно перпендикулярными сторонами.
Коэффициент подобия k
где t – некоторое число.
АВ r1 5
АВ 5t , ВС 12t ,
ВС r2 12

6.

АВD ~ АСВ
Они прямоугольные, А общий
Из треугольника АВС по теореме Пифагора
АС 25t 2 144t 2 АС 13t.
В
D
А
о1
о
2
В
А
r1 АВ 5t 5
Коэффициент подобия равен f
,
R АС 13t 13
13
13
R r1 13.
5
5
Ответ: радиус окружности, вписанной в треугольник АВС, равен 13.
С

7. Задача 2

Дан треугольник АВС со сторонами АС = 12, ВС = 5,
АВ = 13. Вокруг этого треугольника описана
окружность S. Точка D является серединой стороны
АС. Построена окружность S1, касающаяся
окружности S в некоторой точке и отрезка АС в
точке D.

8. Решение

k2
С
D
А
O
В
k1

9.

2
2
2
Треугольник АВС – прямоугольный, так как АВ АС ВС ,
(169 = 144 + 25) – по условию.
Центр О описанной вокруг треугольника АВС окружности
S лежит на середине гипотенузы АВ и, следовательно,
радиус этой окружности R
АВ
6,5см.
2
1
DO ВС 2,5см средняя линия треугольника АВС.
2

10.

Условию задачи удовлетворяют две окружности:
с центром k1иk2
.
Из рисунка видно,
что 2r2 OD R r2
2r2 2r1 2R r1 R r2 4,5см.
Ответ: r1 4,5см; r2 2см.
R OD
2см,
2

11. Задача 3

• Найдите длины двух смежных сторон
параллелограмма, если известно, что их сумма
равна 8, а сумма квадратов длин диагоналей
параллелограмма равна 68.

12. Решение

В
А
С
D
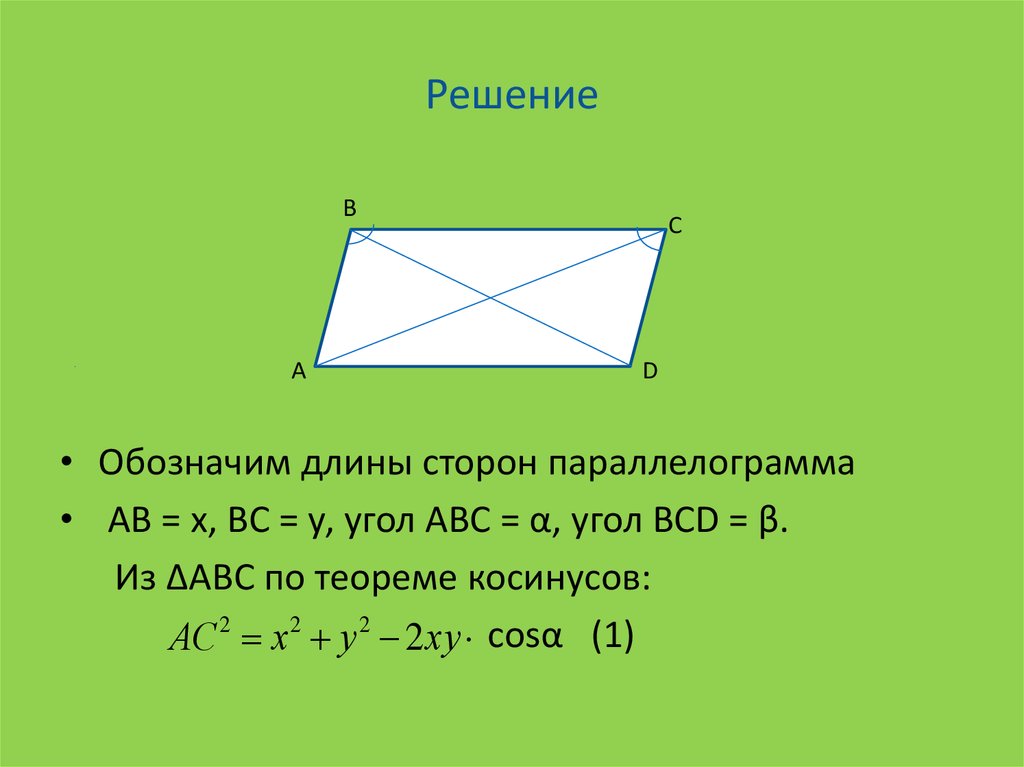
• Обозначим длины сторон параллелограмма
• АВ = х, ВС = у, угол АВС = α, угол ВСD = β.
Из ∆АВС по теореме косинусов:
2
2
2
АС х у 2 ху cosα (1)

13.

• Из ∆ВСD по теореме косинусов:
• BD 2 у 2 х 2 2 ху cosβ (2).
0
• Так как α + β = 180 (по свойству параллелограмма)
0
• cosβ = cos (180 – α) = - cosα ( по формулам
приведения). С учетом этого, после сложения
равенств (1) и (2) получим: АС 2 ВD 2 2( х2 у 2 )
• По условию х + у = 8 и АС 2 BD 2 68.