Планиметрия. Повторение. Часть 1

1.

2.

Часто знает и дошкольник,
Что такое треугольник,
А уж вам-то, как не знать…
Но совсем другое дело –
Очень быстро и умело
Треугольники считать!

3.

Определите своё эмоциональное состояние в
начале урока. Поставьте галочку в клетку,
соответствующую настроению

4.

По сторонам
Разносторонний
Равнобедренный
Равносторонний
По углам
Остроугольный
Тупоугольный
Прямоугольный

5. Разносторонний треугольник

b
a
c
Длины всех сторон разные

6. Равнобедренный треугольник

СВОЙСТВА:
Боковые стороны
b
b
а
2. Высота,
1.
Углы припроведенная
основании равны
к
основанию, является и
медианой и биссектрисой.
Основание

7. Равносторонний треугольник

СВОЙСТВА:
а
а
Все высоты являются
одновременно медианами и
биссектрисами
Все углы равны по
60
а
Точка их пересечения является центром вписанной и
описанной окружностей

8. Классификация по углам:

остроугольный треугольник, в котором все углы острые;
тупоугольный треугольник, в котором один из углов
тупой;
прямоугольный треугольник, в котором один из углов
прямой;
косоугольный треугольник, который не содержит ни
одного прямого угла.

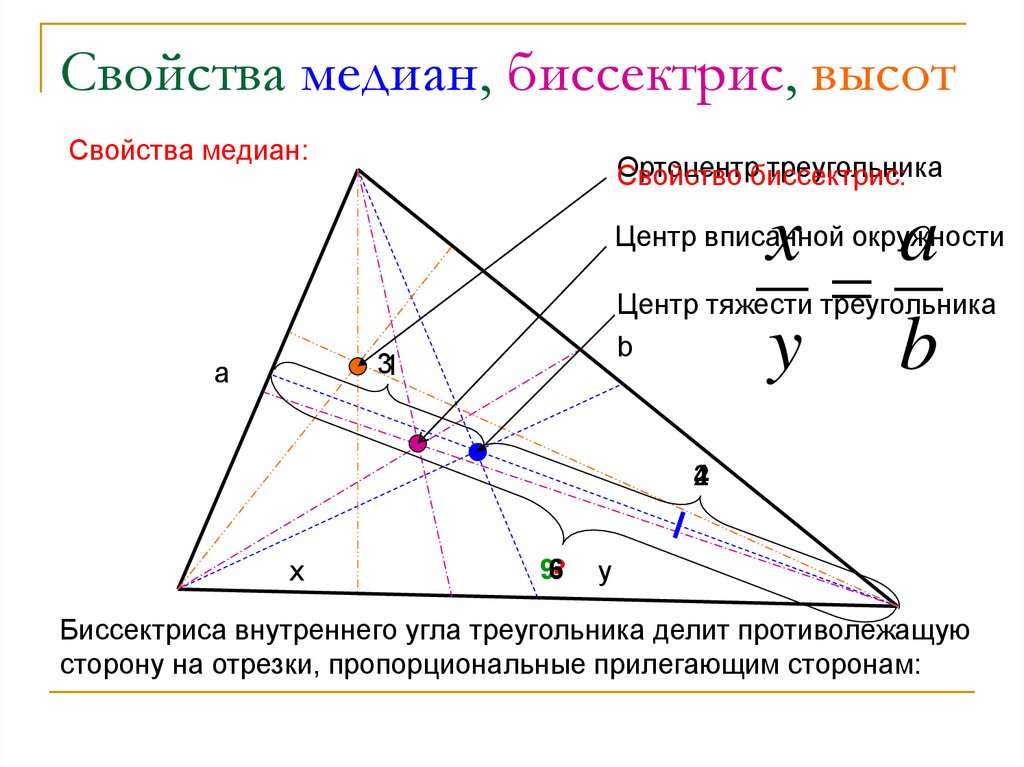
9. Свойства медиан, биссектрис, высот

Свойства медиан:
Ортоцентр
треугольника
Свойство биссектрис:
x a
y b
Центр вписанной окружности
Центр тяжести треугольника
b
31
а
2
4
x
96
?
y
Биссектриса внутреннего угла треугольника делит противолежащую
сторону на отрезки, пропорциональные прилегающим сторонам:

10. «Решение треугольников»

Что это значит?

11. Определение

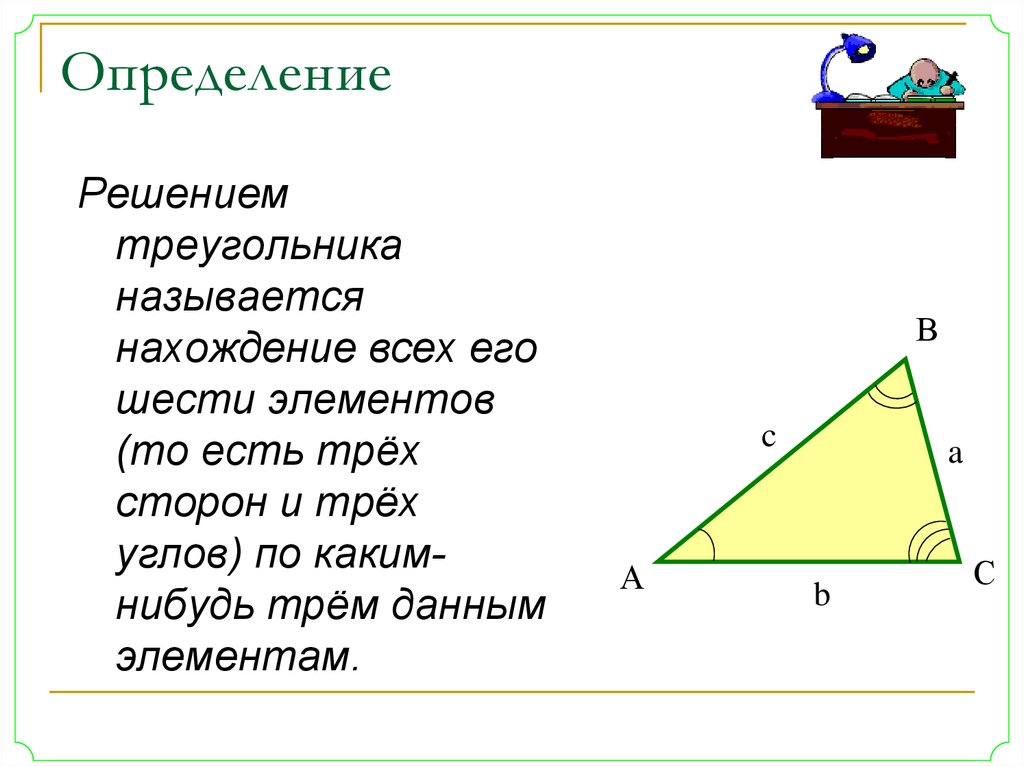
Решением
треугольника
называется
нахождение всех его
шести элементов
(то есть трёх
сторон и трёх
углов) по какимнибудь трём данным
элементам.
В
c
А
a
b
С

12. Три типа задач на решение треугольника

Решение треугольника по двум сторонам и
углу между ними;
Решение треугольника по стороне и
прилежащим к ней углам;
Решение треугольника по трем сторонам.

13. Для этого вспомним

Решение данных задач основано на использовании теорем синуса и
косинуса, теоремы о сумме углов треугольника и следствии из
теоремы синусов.
Причем, при вычислении углов треугольника предпочтительнее
использовать теорему косинусов, а не теорему синусов.
1.
2.
3.
4.
Сумма углов треугольника.
Соотношения между сторонами и углами в треугольнике.
Теорема косинусов.
Теорема синусов.

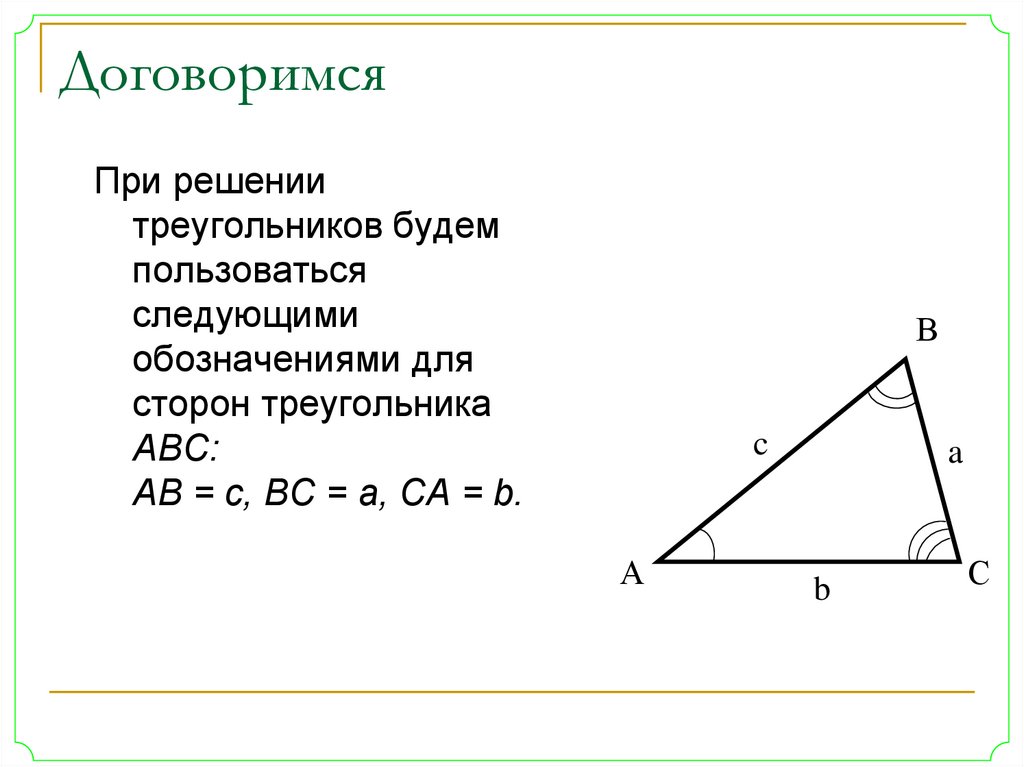
14. Договоримся

При решении
треугольников будем
пользоваться
следующими
обозначениями для
сторон треугольника
ABC:
АВ = с, ВС = а, СА = b.
В
c
А
a
b
С

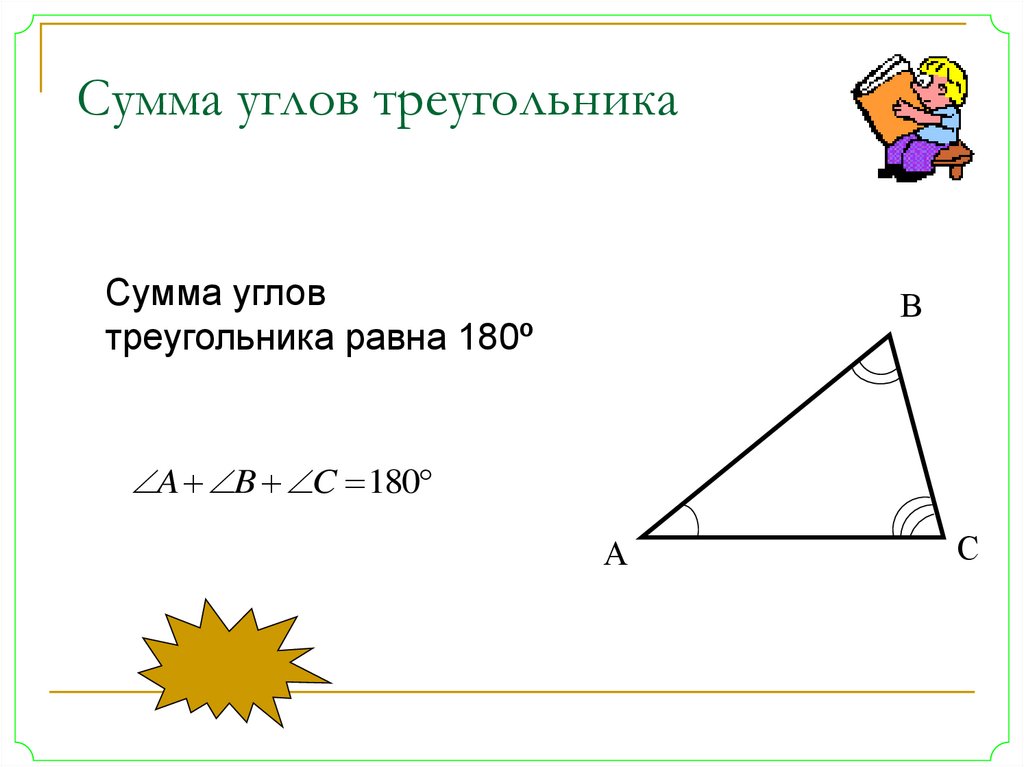
15. Сумма углов треугольника

Сумма углов
треугольника равна 180º
В
A B C 180
А
С

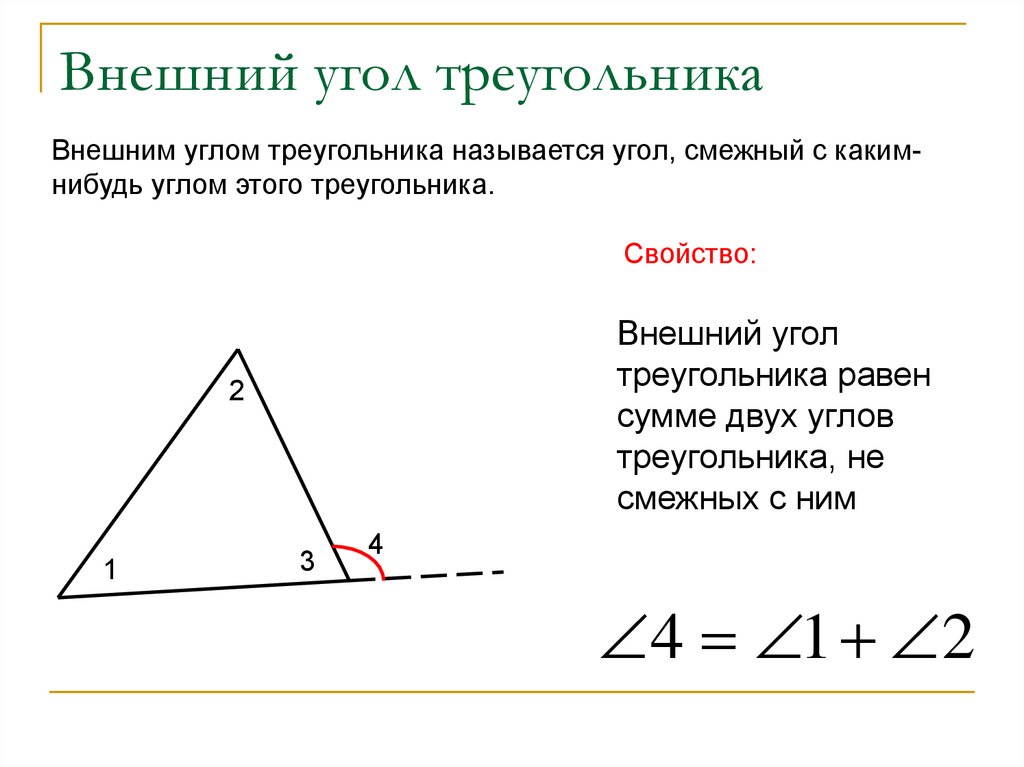
16. Внешний угол треугольника

Внешним углом треугольника называется угол, смежный с какимнибудь углом этого треугольника.
Свойство:
Внешний угол
треугольника равен
сумме двух углов
треугольника, не
смежных с ним
2
1
3
4
4 1 2

17.

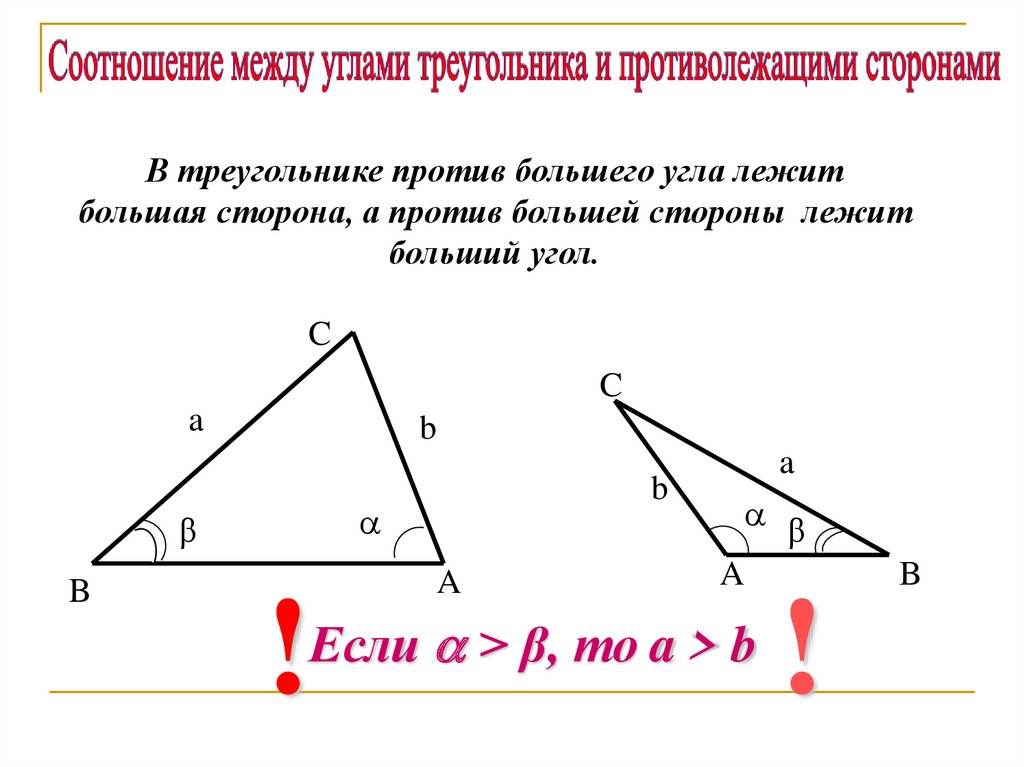
В треугольнике против большего угла лежит
большая сторона, а против большей стороны лежит
больший угол.
C
C
a
b
B
b
β
!
a
A
β
A
Если > β, то a > b
B
!

18. Неравенство треугольника

Каждая сторона треугольника меньше
суммы двух других сторон.
Пусть a, b, c – длины сторон треугольника.
Тогда
a+b>c, a+c>b, c+b>a.

19.

И
И
Л
И
Л
Л
И
1. В треугольнике против угла в 150º лежит большая
сторона.
2. В равностороннем треугольнике внутренние углы
равны между собой и каждый равен 60º.
3. Существует треугольник со сторонами 2 см, 7 см, 3
см.
4. Прямоугольный равнобедренный треугольник имеет
равные катеты.
5. Сумма длин двух сторон любого треугольника
меньше третьей стороны.
6. Существует треугольник с двумя тупыми углами.
7. В прямоугольном треугольнике сумма острых углов
равна 90º.

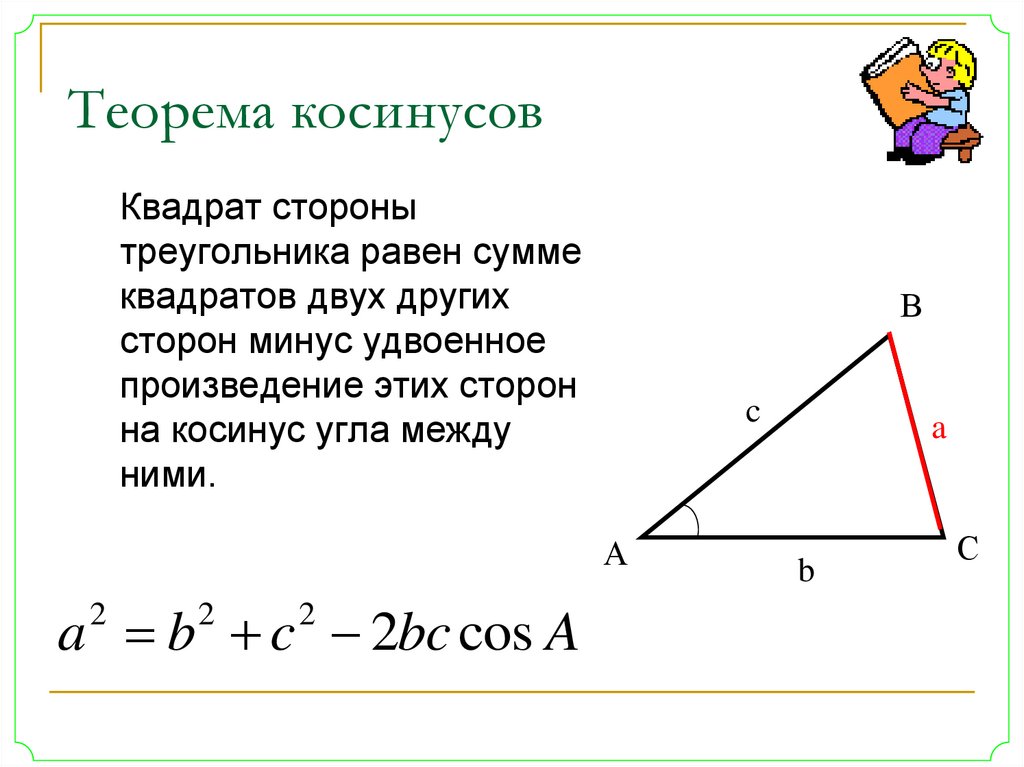
20. Теорема косинусов

Квадрат стороны
треугольника равен сумме
квадратов двух других
сторон минус удвоенное
произведение этих сторон
на косинус угла между
ними.
В
c
А
a b c 2bc cos A
2
2
2
a
b
С

21. Определение вида треугольника

Из формулы, следующей из теоремы косинусов, примененной к
наибольшему углу, учитывая знак косинуса, можно получить
соотношения между квадратами сторон, позволяющие определить вид
треугольника.
Выразим cos A из формулы:
a 2 b 2 c 2 2bc cos A
b 2 c 2 a 2 . Так как b, c >0, то:
получим cos A
2bc
2
2
2
2
2
2
a
b
c
,
т.е
b
c
a
0
• если cos А < 0, то
2
2
2
• если cos А > 0, то b c a 0, т.е a b c
2
2
2
2
• если cos А = 0, то b c a 0, т.е a b c
2
2
2
2
2
Следовательно, треугольник, у которого a – наибольшая сторона, будет:
• тупоугольный, если
a2 b2 c2
• остроугольный, если
a2 b2 c2
• прямоугольный, если
a2 b2 c2

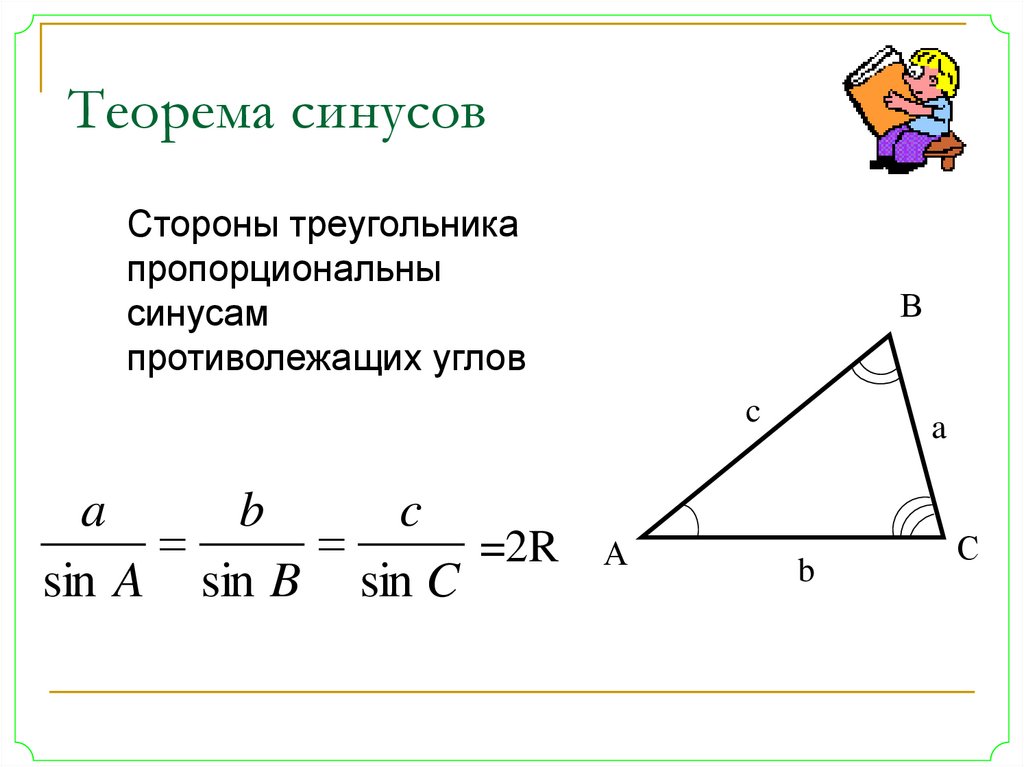
22. Теорема синусов

Стороны треугольника
пропорциональны
синусам
противолежащих углов
В
c
a
b
c
=2R
sin A sin B sin C
А
a
b
С

23. Задача 1. Решение треугольника по двум сторонам и углу между ними

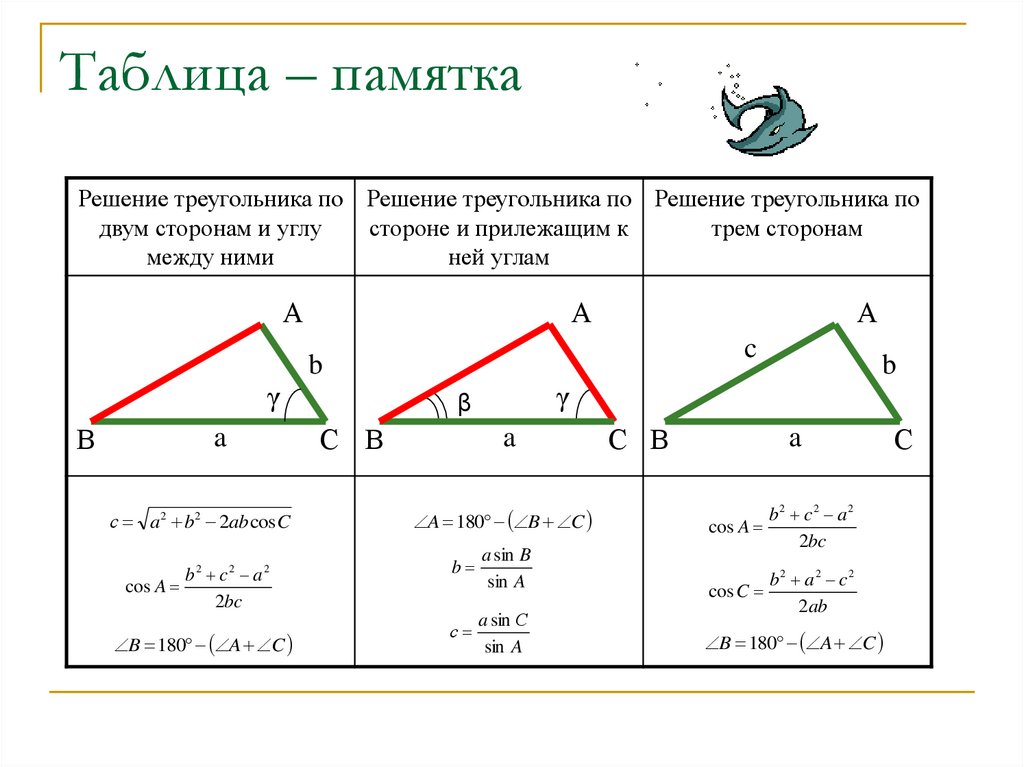
Таблица – памятка
Решение треугольника по Решение треугольника по Решение треугольника по
двум сторонам и углу
стороне и прилежащим к
трем сторонам
между ними
ней углам
А
А
А
c
b
γ
В
a
с a 2 b2 2ab cos C
γ
β
С В
a
A 180 B C
b2 c2 a 2
cos A
2bc
b
B 180 A C
с
b
a sin B
sin A
a sin С
sin A
С В
a
cos A
b2 c2 a 2
2bc
cos C
b2 a 2 c2
2ab
B 180 A C
С

24. Задача 2. Решение треугольника по стороне и прилежащим к ней углам

Задачи для самостоятельного решения
1. АС=5м, АВ=6 м, cos A=0,6. Найти ВС.
2. АС= 5 м, АВ= 6 м, ВС= 7 м. Найти cos А.
3. Угол А равен 45 градусов, угол В равен 60 градусов, ВС=3 м.
Найти АС.
4. Найдите стороны треугольника АВС, если А 45 , С 30 ,
а высота AD равна 3 м.
5. Найдите острый угол между
биссектрисами острых углов
прямоугольного треугольника. Ответ
дайте в градусах.

25. Задача 3. Решение треугольника по трём сторонам

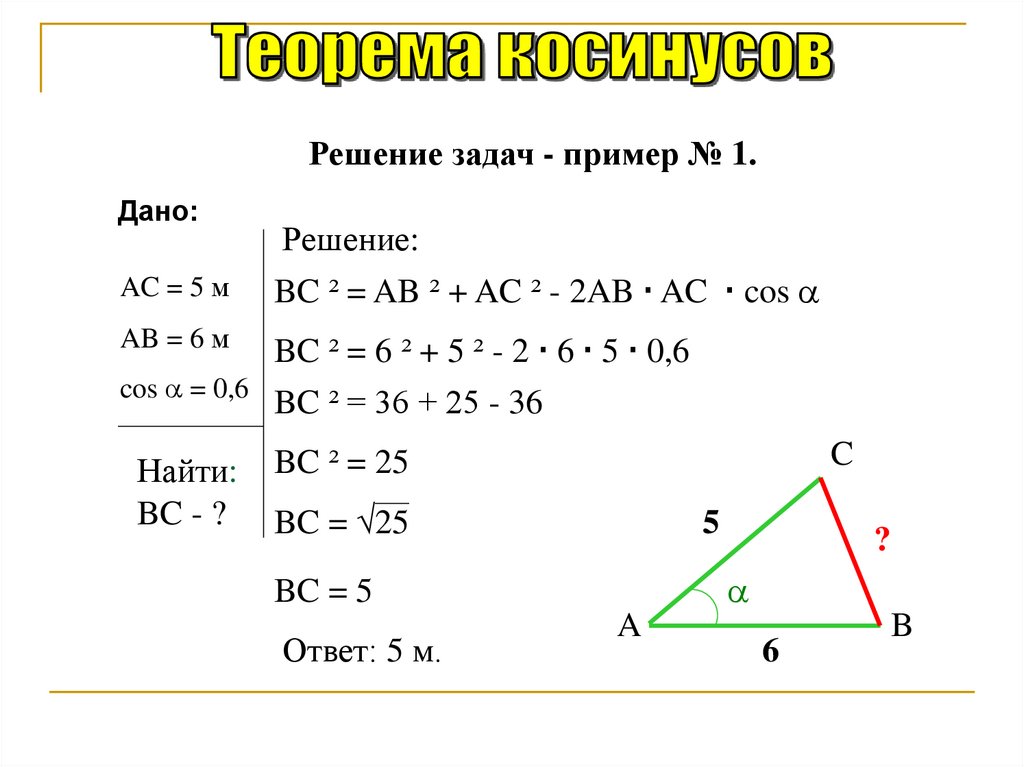
Решение задач - пример № 1.
Дано:
AC = 5 м
Решение:
BC ² = AB ² + AC ² - 2AB AC cos
AB = 6 м
BC ² = 6 ² + 5 ² - 2 6 5 0,6
cos = 0,6
BC ² = 36 + 25 - 36
Найти:
BC - ?
C
BC ² = 25
BC = 25
5
BC = 5
Ответ: 5 м.
?
A
6
B

26. Таблица – памятка

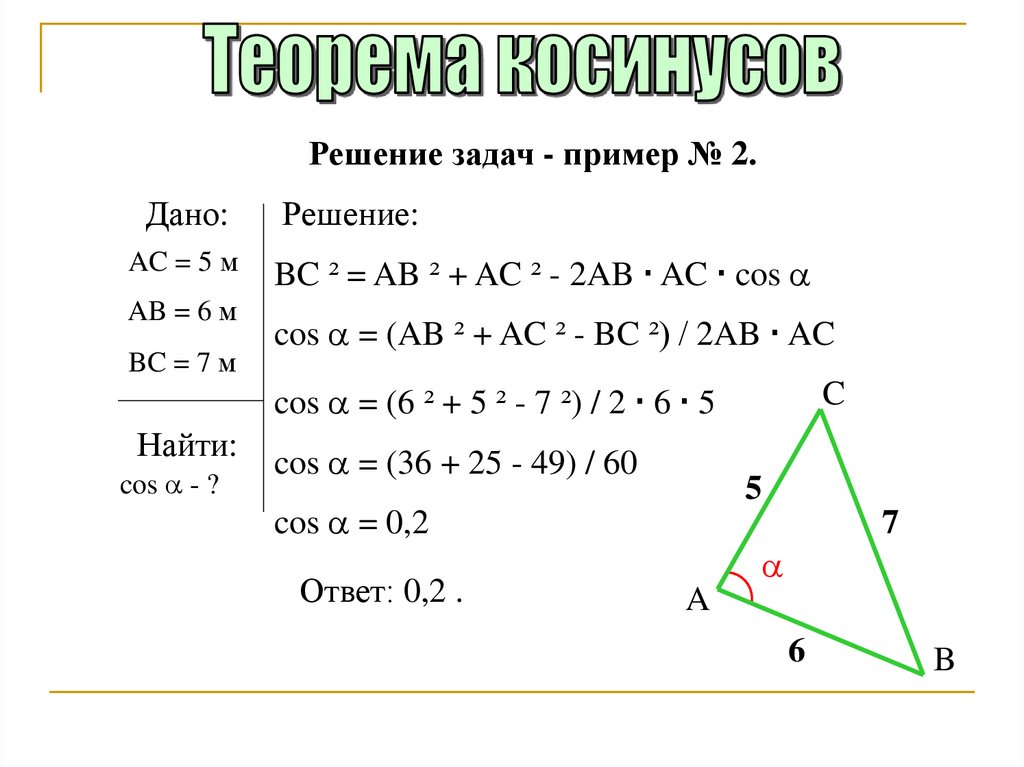
Решение задач - пример № 2.
Дано:
AC = 5 м
AB = 6 м
BC = 7 м
Решение:
BC ² = AB ² + AC ² - 2AB AC cos
cos = (AB ² + AC ² - BC ²) / 2AB AC
cos = (6 ² + 5 ² - 7 ²) / 2 6 5
Найти:
cos - ?
cos = (36 + 25 - 49) / 60
5
cos = 0,2
Ответ: 0,2 .
C
7
A
6
B

27. Задачи для самостоятельного решения

Решение задач - пример № 3.
Дано:
= 45°
β = 60°
a=3м
Найти:
b-?
Решение:
a/sin =b/sin β
b= a sin β/ sin
b = 3 sin 60° / sin 45°
B
b = 3 ( 3 / 2) / (1 / 2 )
b = 3 6 / 2
c
a
A
Ответ: 3 6 / 2
β
b
C

28.

Математическая пауза

29.

ПЛОЩАДЬ
ТРЕУГОЛЬНИКА

30.

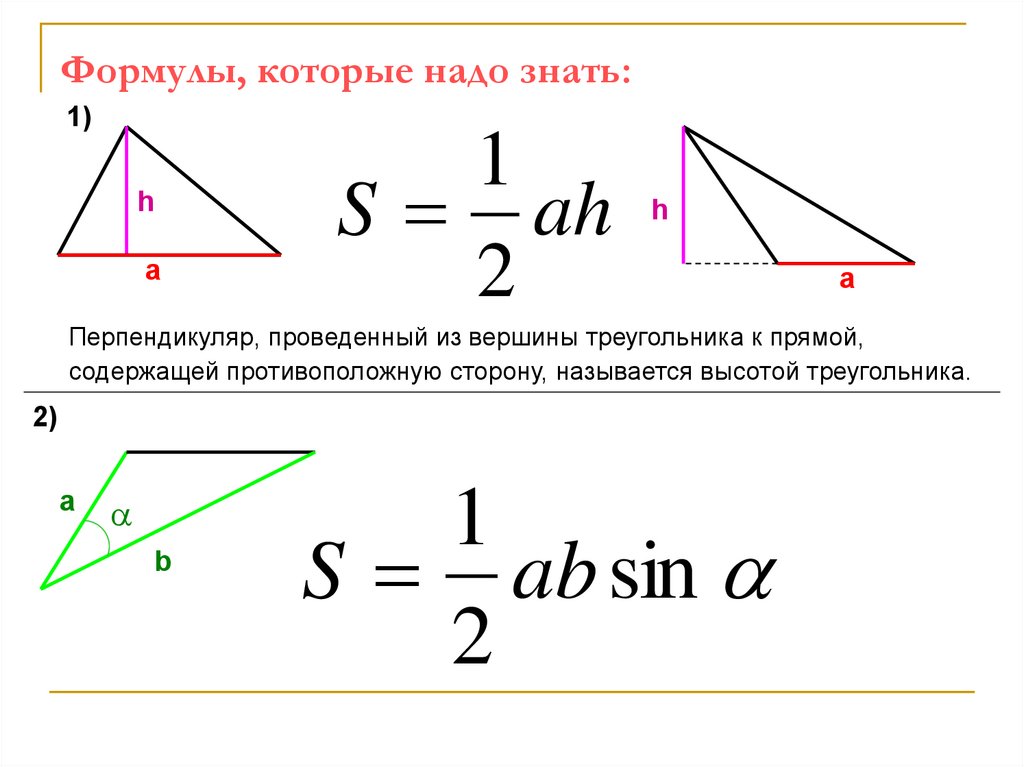
Формулы, которые надо знать:
1)
h
а
1
S ah
2
h
а
Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой треугольника.
2)
а
b
1
S ab sin
2

31. Математическая пауза

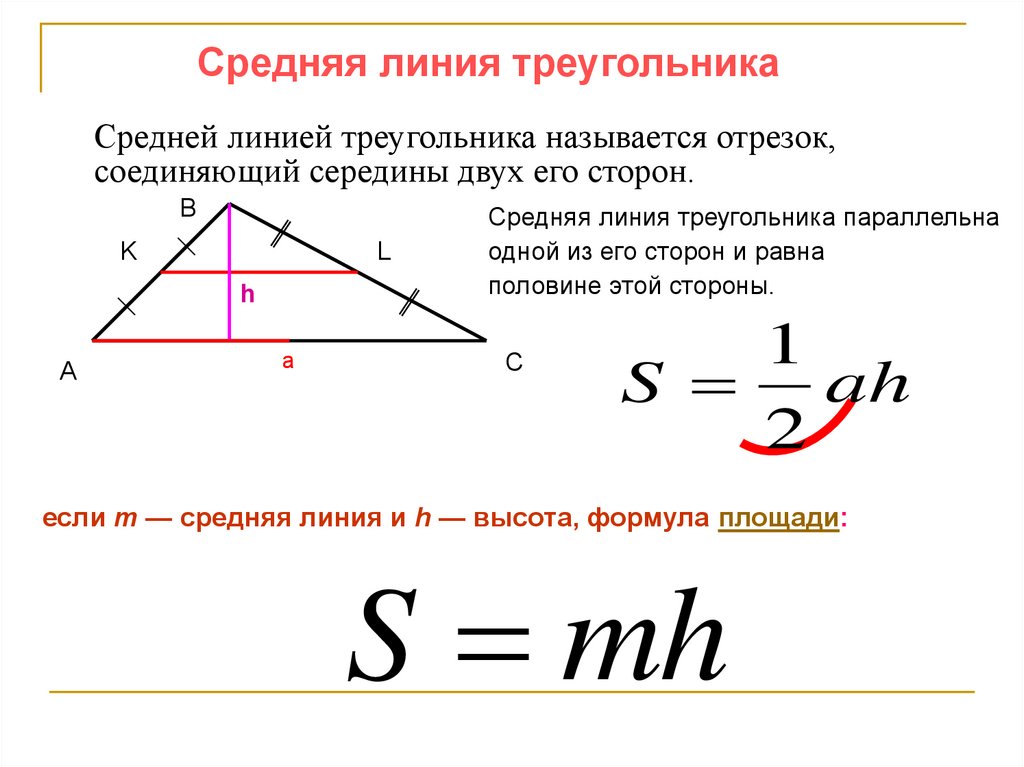
Средняя линия треугольника
Средней линией треугольника называется отрезок,
соединяющий середины двух его сторон.
B
K
L
h
А
а
Средняя линия треугольника параллельна
одной из его сторон и равна
половине этой стороны.
C
1
S ah
2
если m — средняя линия и h — высота, формула площади:
S mh

32.

3) Формула
Герона
b
а
c
S p(p a)(p b)(p c);
где p – полупериметр треугольника

33. Формулы, которые надо знать:

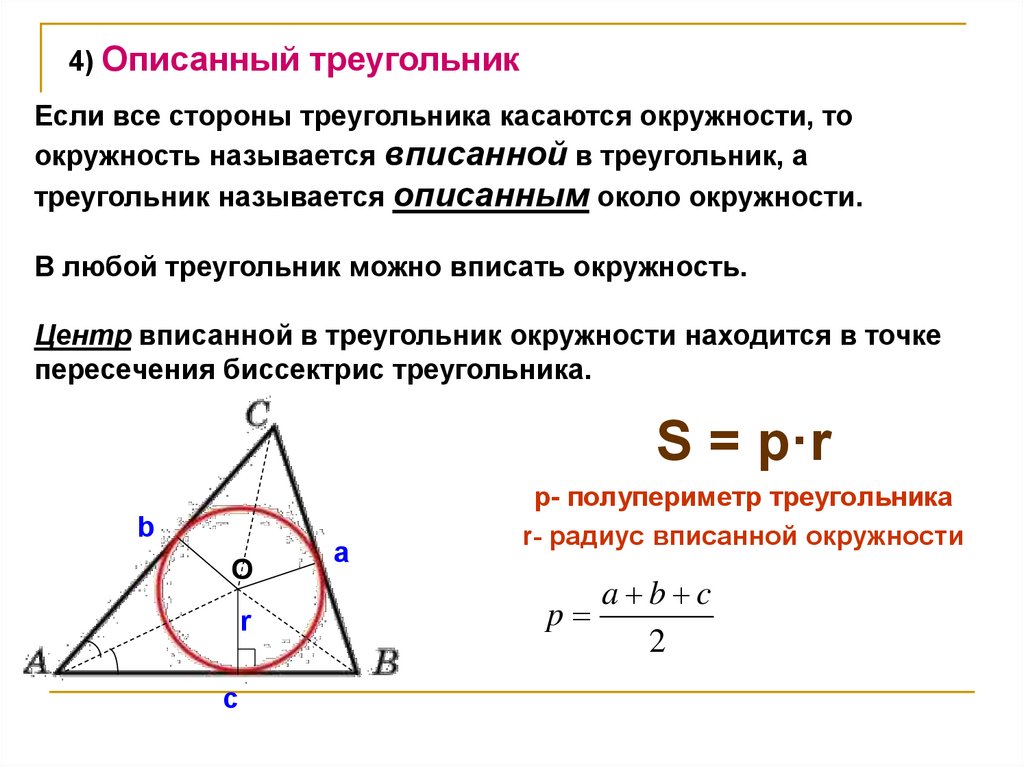
4) Описанный треугольник
Если все стороны треугольника касаются окружности, то
окружность называется вписанной в треугольник, а
треугольник называется описанным около окружности.
В любой треугольник можно вписать окружность.
Центр вписанной в треугольник окружности находится в точке
пересечения биссектрис треугольника.
S = p·r
b
О
r
c
a
p- полупериметр треугольника
r- радиус вписанной окружности
p
a b c
2

34.

5) Вписанный треугольник
Если все вершины треугольника лежат на окружности, то
окружность называется описанной около треугольника, а
треугольник называется вписанным в окружность.
Около любого треугольника можно описать окружность.
Центр описанной около треугольника окружности находится в
точке пересечения перпендикуляров, проведенных через
середины сторон треугольника.
a b c
S
4R

35. 3) Формула Герона

B
A
D
Е F
C

36.

1. ЧТЕНИЕ УСЛОВИЯ ЗАДАЧИ.
2. ВЫПОЛНЕНИЕ ЧЕРТЕЖА С БУКВЕННЫМИ
ОБОЗНАЧЕНИЯМИ.
3. КРАТКАЯ ЗАПИСЬ УСЛОВИЯ ЗАДАЧИ
(ФОРМИРОВАНИЕ БАЗЫ ДАННЫХ).
4. ПЕРЕНОС ДАННЫХ УСЛОВИЯ НА ЧЕРТЕЖ;
ВЫДЕЛЕНИЕ ЭЛЕМЕНТОВ ЧЕРТЕЖА
РАЗЛИЧНЫМИ ЦВЕТАМИ.
5. 3АПИСЬ ТРЕБУЕМЫХ ФОРМУЛ И ТЕОРЕМ НА
ЧЕРНОВИКЕ (ФОРМИРОВАНИЕ БАЗЫ ЗНАНИЙ).

37.

6. «ДЕТАЛИРОВКА» — ВЫЧЕРЧИВАНИЕ ОТДЕЛЬНЫХ
ДЕТАЛЕЙ НА ДОПОЛНИТЕЛЬНЫХ ЧЕРТЕЖАХ.
7. АНАЛИЗ ДАННЫХ ЗАДАЧИ, ПРИВЯЗКА ИСКОМЫХ
ВЕЛИЧИН К ЭЛЕМЕНТАМ ЧЕРТЕЖА.
8. «СИНТЕЗ» — СОСТАВЛЕНИЕ «ЦЕПОЧКИ»
ДЕЙСТВИЙ (АЛГОРИТМА РЕШЕНИЯ).
9. РЕАЛИЗАЦИЯ АЛГОРИТМА РЕШЕНИЯ.
10. ПРОВЕРКА ПРАВИЛЬНОСТИ РЕШЕНИЯ.
11. ЗАПИСЬ ОТВЕТА.

38.

Дано:
В треугольнике АВС
АВ=с=13 см;
ВС=а=14 см;
АС=b=15 см.
Найти:
1) площадь S;
2) hb − высоту BD;
3) радиус вписанной окружности r;
4) величину наибольшего
внутреннего угла треугольника
АВС;
5) радиус описанной окружности R;
6) mb − длину медианы BF;
7) Lb − длину биссектрисы ВЕ угла
В (точка Е лежит на отрезке АС).
В
13
А
14
D E
15
F
С

39.

1. Вычисление площади треугольника АВС.
База знаний.
Выпишем формулы, по которым можно найти площадь
треугольника:
1
S b hb ;
(1)
2
S
1
a c sin B;
2
S p(p a)(p b)(p c);
S r p,
1
p
(a b c) — полупериметр треугольника АВС.
где
2
(2)
(3)
(4)

40.

Поскольку в условии задачи даны только длины
сторон треугольника АВС, то для вычисления его
площади нам необходимо воспользоваться именно
формулой Герона (3).
Вычислим сначала полупериметр треугольника:
1
1
p (a b c) (13 14 15) 21(см).
2
2
2
S
21
8
7
6
84
(
см
).
Тогда, по формуле (3),
S p(p a)(p b)(p c);
(3)

41.

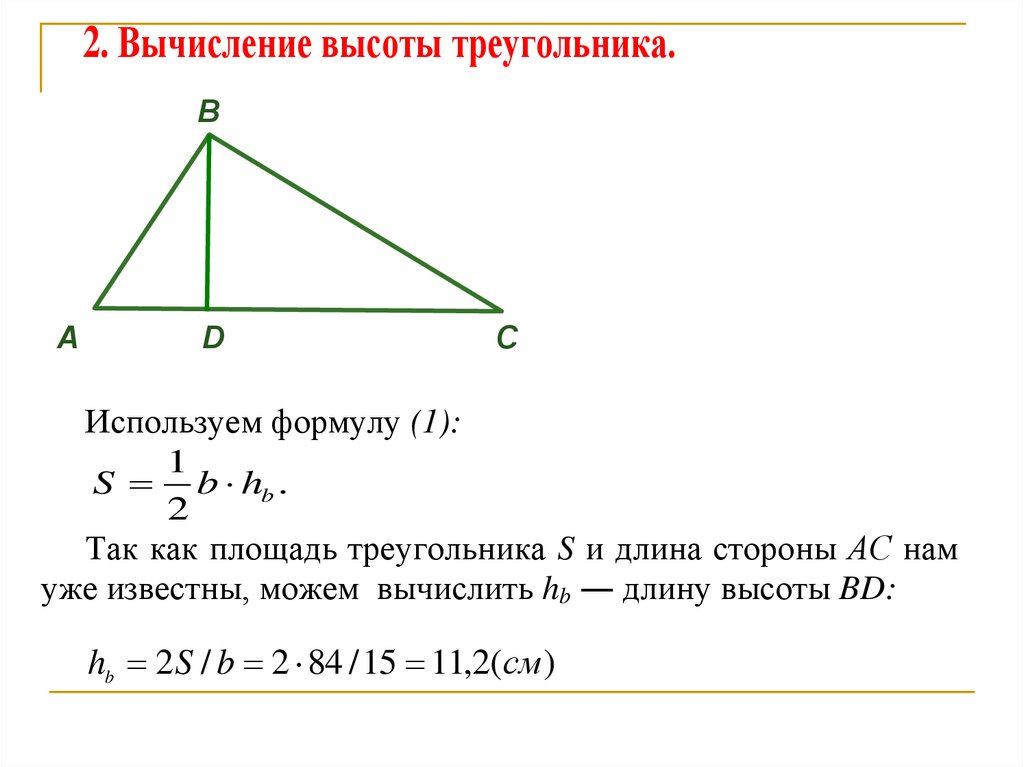
2. Вычисление высоты треугольника.
B
А
D
C
Используем формулу (1):
1
S b hb .
2
Так как площадь треугольника S и длина стороны АС нам
уже известны, можем вычислить hb ― длину высоты BD:
hb 2 S / b 2 84 / 15 11,2(см )

42.

3. Вычисление радиуса вписанной окружности.
B
А
C
Для
вычисления
длины
r
радиуса
вписанной
окружности нам необходимо воспользоваться формулой
площади треугольника (4):
S p r .
Отсюда
находим
r S : p 84 : 21 4(см).

43.

4. Вычисление наибольшего угла треугольника.
Включаем в базу знаний теорему о том, что против большей
стороны в треугольнике лежит больший угол.
Из этой теоремы следует, что большим углом в треугольнике
АВС является угол В. По формуле (2) можем записать:
1
S a c sin B.
2
2 84 12
2S
sin B
a c 13 14 13

44.

5. Вычисление радиуса описанной окружности.
Ответ на вопрос задачи о вычислении длины R радиуса
описанной окружности требует включения в базу знаний
теоремы синусов:
a
b
c
a b c
2 R.
sin A sin B sin C
2S
(6)
Из соотношения (6) следует, что
b
15 13 65
R
(см).
2 sin B 2 12
8
Этот же результат можно получить, подставляя длины
сторон и площадь треугольника в другую формулу, также
следующую из (6):
(5)
R
a b c 13 14 15 65
(см).
4S
4 84
8

45.

6. Вычисление длины медианы треугольника.
Построим медиану BF и вычислим ее длину mb.
Для этого добавим в базу знаний теорему косинусов,
согласно которой в треугольнике АВС:
a 2 b 2 c 2 2bc cos A.
(7)
B
c
А
m
b
a
F
C
Дважды применим теорему косинусов, применив ее сначала к
треугольнику АВС, а затем к треугольнику АВF.
b2 c 2 a 2
cos A
Значение cosA находим из формулы (7):
2bc

46.

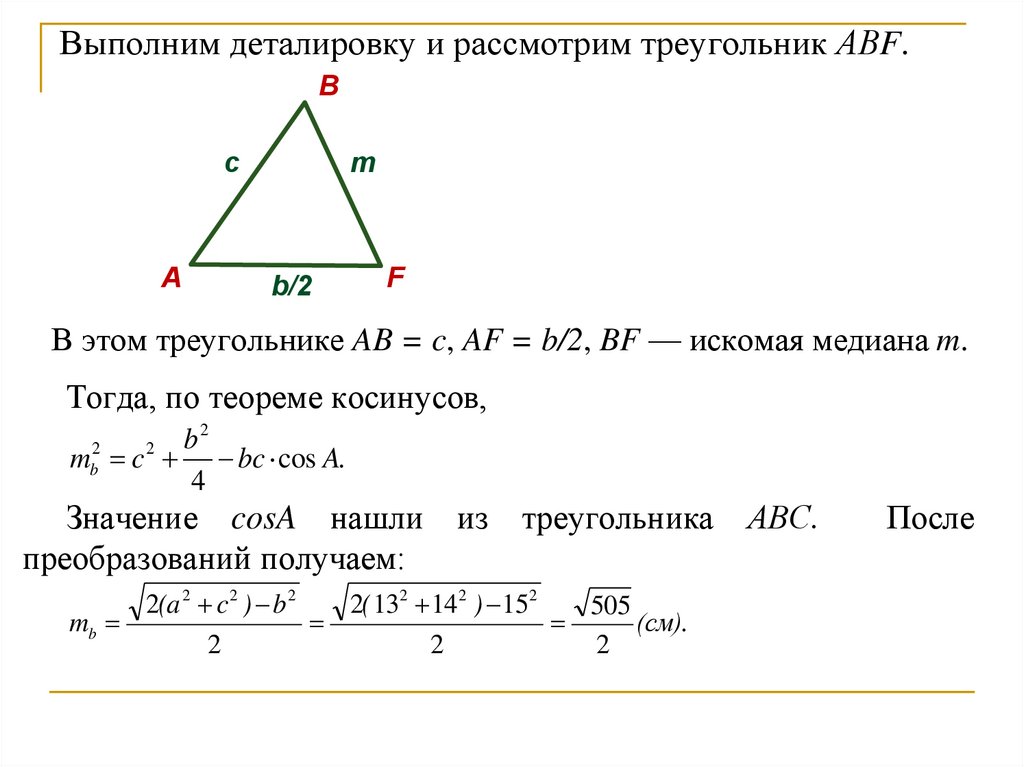
Выполним деталировку и рассмотрим треугольник АВF.
B
c
А
m
b/2
F
В этом треугольнике AB = c, AF = b/2, BF — искомая медиана m.
Тогда, по теореме косинусов,
b2
m c bc cos A.
4
2
b
2
Значение cosA нашли из треугольника АВС.
преобразований получаем:
2(a 2 c 2 ) b 2
2( 132 14 2 ) 152
505
mb
(см).
2
2
2
После

47.

Длину медианы можно также получить, достроив треугольник
АВС до параллелограмма АВСК, в котором АС является диагональю,
а BF — половиной другой диагонали.
Тогда для вычисления mb можно воспользоваться тем, что сумма
квадратов диагоналей параллелограмма равна сумме квадратов всех
его сторон
(этот факт также добавляем в базу знаний):
A
c
a
K
b m
c
F
m
B
a
C
(2mb ) 2 b 2 2a 2 2c 2 ,
отсюда
2(a 2 c 2 ) b 2
mb
.
2

48.

7. Вычисление длины биссектрисы треугольника.
Построим биссектрису BЕ и вычислим ее длину Lb по схеме,
описанной в предыдущем пункте.
B
А
E
C
Дополнительное затруднение связано с необходимостью вычисления
длины отрезка AE. Найти ее нам помогает следующая теорема,
включаемвя в базу знаний:
Биссектриса внутреннего угла треугольника делит
противолежащую сторону на части, пропорциональные
сторонам, образующим этот угол: АЕ / ЕС = АВ / ВС.

49.

Обозначим AE = x
, тогда EC = b –
- xx.
Из упомянутой теоремы следует
пропорция: x b x
c
a
bc
x
Отсюда находим:
a c
В
c
А
L
a
Е
С
2
L
Используя теорему косинусов, из треугольника АВЕ выражаем
b :
L2b c 2 x 2 2cx cos A
После преобразований получаем:
ac((a c)2 b 2 )
13 14(( 13 14 )2 152 ) 28 13
Lb
(см).
a c
13 14
9
Отметим, что при выводе формул для вычисления
применяются тождества сокращенного умножения,
которые также должны быть включены в базу знаний.

50.

ПРОВЕРКА.
1. Размерности всех результатов верны.
2. Все заданные величины использованы при решении задачи.
ОТВЕТ.
Поскольку каждому этапу определения искомых величин при
решении присвоен номер, соответствующий номеру в условии задачи,
мы не будем выписывать ответы в отдельном пункте.

51.

52.

1.Вычисление площади треугольника.
1
S b hb ;
2
1
S a c sin B;
2
(1)
(2)
S p(p a)(p b)(p c);
S r p,
где r - радиус вписанной окружности,
p
S
a b c
4R
(3)
(4)
,
1
(a b c)
2
— полупериметр треугольника.
где R - радиус описанной окружности.
(5)
2. Теорема синусов.
a
b
c
a b c
a b c
2 R. ( R
)
sin A sin B sin C
2S
4S
2
2
2
a
b
c
2bc cos A.
3. Теорема косинусов:
(6)
(7)

53.

4. Параллелограмм.
Сумма квадратов диагоналей параллелограмма равна
сумме квадратов всех его сторон.
5. Биссектриса внутреннего угла треугольника.
Биссектриса внутреннего угла треугольника делит
противолежащую
сторону
на
части,
пропорциональные сторонам, образующим этот угол:
АЕ / ЕС = АВ / ВС.
В
А
E
C

54.

Задание на дом
1. Найдите медиану и биссектрису большего угла треугольника АВС,
если его стороны равны 4 см, 6 см и 8 см.
2. В треугольнике АВС известна сторона а, противолежащий ей угол α,
угол β. Найдите третий угол γ треугольника, длины сторон b и c,
радиус описанной окружности R, радиус вписанной окружности r.
а 6 2
,
45 , 30
3(*). В равнобедренном треугольнике боковые стороны равны 17, а
основание равно 30. Найдите:
а) высоту, проведенную к боковой стороне;
б) синус угла между равными сторонами;
в) отношение радиуса вписанной окружности к радиусу описанной
окружности;
г) медиану, проведенную к боковой стороне;
д) биссектрису, проведенную к боковой стороне.

55.

Дополнительное задание.

56.

Психологическая заминка
Урок заканчивается, пожалуйста определите своё
эмоциональное состояние в конце урока. Поставьте на этой
же карточке галочку в клетку, соответствующую настроению

57. Задание на дом

Спасибо за урок! Успехов!