Решение треугольников

1. Решение треугольников

А
b
h
γ
С
a
А
с
с
α
b
γ
В
С
β
a
В

2. Содержание

Теорема о площади треугольника
Теорема синусов
Теорема косинусов
Задача № 1
Задача № 2
Задача № 3
Решение задач

3. Теорема о площади треугольника

Площадь треугольника равна половине
произведения двух его сторон на синус
угла между ними
А
b
С
h
a Н
Дано: ∆АВС
Доказать:
S∆ABC = 1 ab sinC
2
Доказательство:
с
В

4. Теорема синусов

Стороны треугольника пропорциональны
синусам противолежащих углов
А
α
b
β
γ
С
с
a
Дано: ∆АВС
Доказать:
а
b
c
=
=
sinα sinβ sinγ
В Доказательство:

5.

Теорема косинусов
Квадрат стороны треугольника равен
сумме квадратов двух других сторон минус
удвоенное произведение этих сторон на
косинус угла между ними.
С
b
Дано: ∆АВС
Доказать:
a
a2 = b2 + с2 – 2bc cosα
α
А
с
В
Доказательство:

6. Задача № 1 Решение треугольника по двум сторонам и углу между ними

В
Дано: ∆АВС, a, b, γ.
с
Найти: с, α, β.
Решение:
А
α
β
γ
а
b
С
1. По теореме косинусов с2 = a2 + b2 – 2ab cos γ.
Откуда с = √a2 + b2 – 2ab cos γ.
2 + c 2 – a2
b
2. По теореме косинусов cos α =
2bc
3. β = 180о − α − γ.

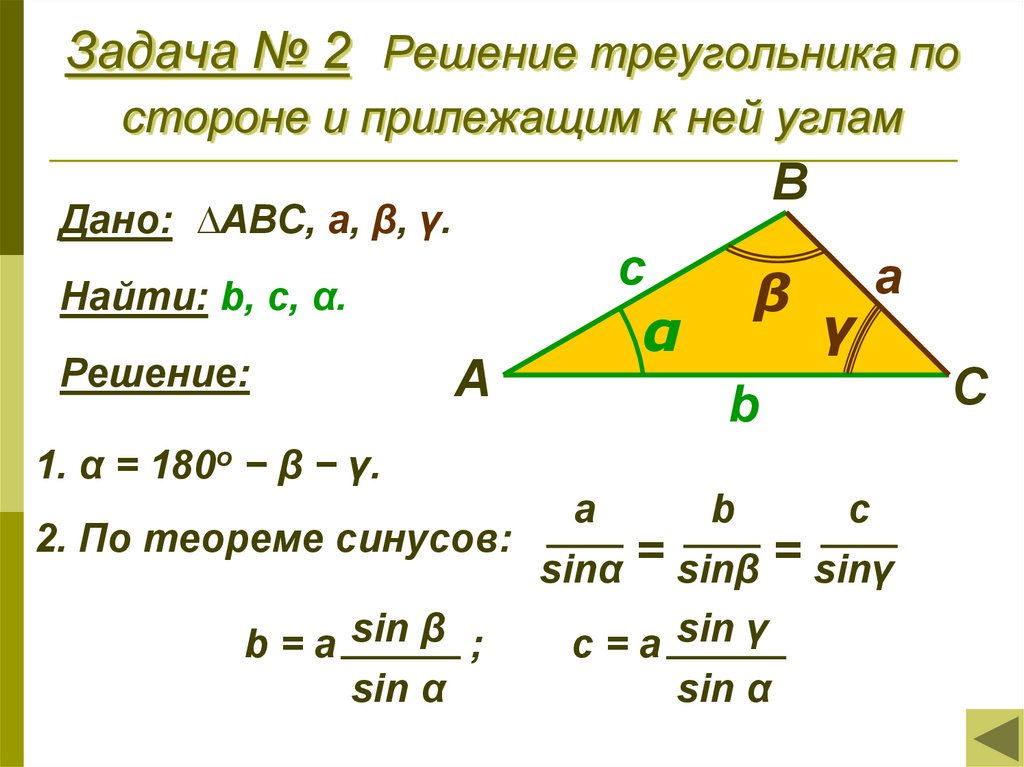
7. Задача № 2 Решение треугольника по стороне и прилежащим к ней углам

В
Дано: ∆АВС, a, β, γ.
с
Найти: b, с, α.
Решение:
α
А
1. α = 180о − β − γ.
2. По теореме синусов:
b = a sin β ;
sin α
β
γ
а
С
b
а
sinα
=
b
sinβ
c = a sin γ
sin α
=
c
sinγ

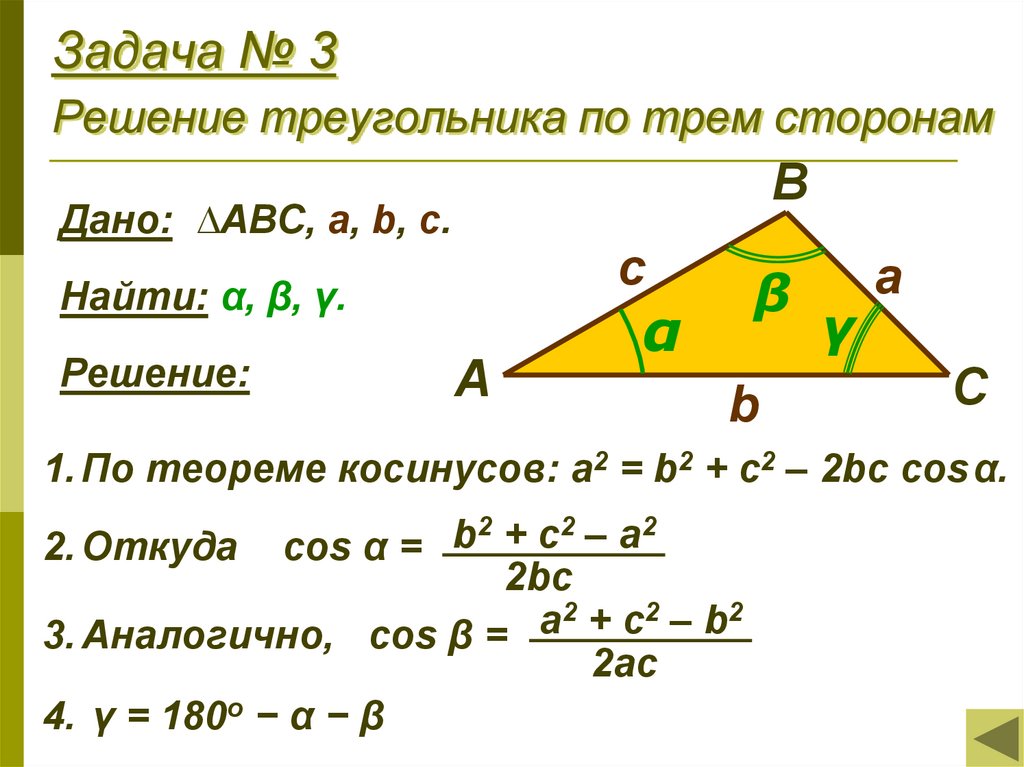
8. Задача № 3 Решение треугольника по трем сторонам

В
Дано: ∆АВС, a, b, с.
с
Найти: α, β, γ.
Решение:
А
β
α
b
γ
а
С
1. По теореме косинусов: a2 = b2 + c2 – 2bc cosα.
2 + c 2 – a2
b
2. Откуда cos α =
2bc
2 + c2 – b2
a
3. Аналогично, cos β =
2ac
4. γ = 180o − α − β

9.

Вариант 1
1. Две стороны треугольника равны соответственно 1 см и 18 см, а угол
между ними составляет 135°. Найдите третью сторону треугольника.
2. В треугольнике ABC A = 60°, B = 45°, АСС = 6 см. Найдите
сторону ВС.
3. Большая диагональ и большая сторона параллелограмма соответственно
равны 19 см и 2 3 см, а его острый угол составляет 30°. Найдите
меньшую сторону параллелограмма.
4. В равнобокой трапеции ABCD с основаниями AD и ВС. ВС = 4 cм,
BDC = 30°, BDA = 45°. Найдите радиус окружности, описанной вокруг
трапеции, и ее боковую сторону.

10. Домашнее задание

Вариант 2
1. Две стороны треугольника равны соответственно 3 см и 8 см, а угол
между ними составляет 60°. Найдите третью сторону треугольника.
2. В остроугольном треугольнике ABC: AB = 3 см, ВС = 2 см, A =
45°. Найдите угол С.
3. Большая диагональ параллелограмма равняется 3 см и образует со
сторонами углы, которые равняются соответственно 15° и 45°. Найдите
большую сторону параллелограмма.
4. Стороны треугольника равны 16 см, 18 см и 26 см. Найдите медиану,
проведенную к большей стороне треугольника.