Similar presentations:
Решение задач по планиметрии
1. «Практические рекомендации к решению задач по планиметрии»
Учитель математики МОУ «Разуменская СОШ №1Белгородского района Белгородской области»
Фуникова Татьяна Николаевна
2.
«Математика- высшая степень
человеческого познания, а геометрия
самое могущественное средство для
поощрения умственных способностей.»
М.В.Ломоносов
3. Цель занятия:
Представление методов и приемовработы, которые могут быть
использованы учителямипредметниками на своих уроках.
4. План занятия
1. Роль геометрии в математическом образованииучащихся.
2. Основные методы решения задач.
3. Система учебных занятий и приемы работы с
учащимися.
4. Базисные задачи.
5. Творческие задачи.
6. Практическое занятие (проверьте себя).
7. Моделирование(самостоятельная работа
слушателей).
8. Рефлексия
5. Эпиграф
«Вдохновение нужно в поэзии так же, как вгеометрии».
А.С.Пушкин
6.
На протяжении веков геометрия служила
источником развития не только математики,
но и других наук. С помощью геометрии
формировались законы математического
мышления. Многие геометрические задачи
способствовали появлению новых научных
направлений(геометрия Н.И.Лобачевского).
7.
Современная геометрия включает много новых
направлений: топология, дифгеометрия, теория графов,
компьютерная. Огромна роль геометрии в развитии
логического мышления учащихся и пространственного
воображения. Именно геометрия дает представление об
истине, учит ее доказывать. Карл Бенц с помощью
равнобокой трапеции изобрел поворот передних колес
автомобиля.
Почему наши ученики боятся геометрию? Почему не
умеют решать задачи?
При решении геометрических задач, выпускники средних
школ проявляют полную беспомощность, которая
свидетельствует не о слабых знаниях, а просто об их
отсутствии. Причины этого очевидны:
1. Геометрия значительно сложнее алгебры
2. Не знание теории
3. Не умение решать базисные задачи
4. Не отработаны все методы решения задач
5. Не умение строить рисунок
8.
Существует 3 основных метода решения
задач: геометрический, алгебраический,
комбинированный.
Все эти методы будут работать только в
одном случае: правильно сделан
рисунок, найдены свойства фигур,
правильно выбран путь к решению
задач.
9. Система учебных занятий.
1) Уроки-лекции2) Уроки-практикумы трех видов: обучающий,
закрепляющий, диагностика.
3) Уроки зачеты
4) Урок одной
5) Урок смотр знаний
10. Приемы работы на уроке геометрии:
Опиши рисунокЗащита реферата
Изучи базисные задачи
Составь план решения задачи
По готовому решению найди свойства
фигур
• Исследуй условие задачи (сколько
решений?)
• Соедини базисные в творческую задачу
• Игра «Задай вопросы друг другу»
11.
Защита реферата
Описать рисунок
Составь план решения
Исследуй условие задачи
12. Некоторые базисные задачи Углы и их свойства
αУгол между
биссектрисами
смежных углов
α
β
Углы со взаимноперпендикулярными
сторонами
α
α=2β
Вписанный,
центральный
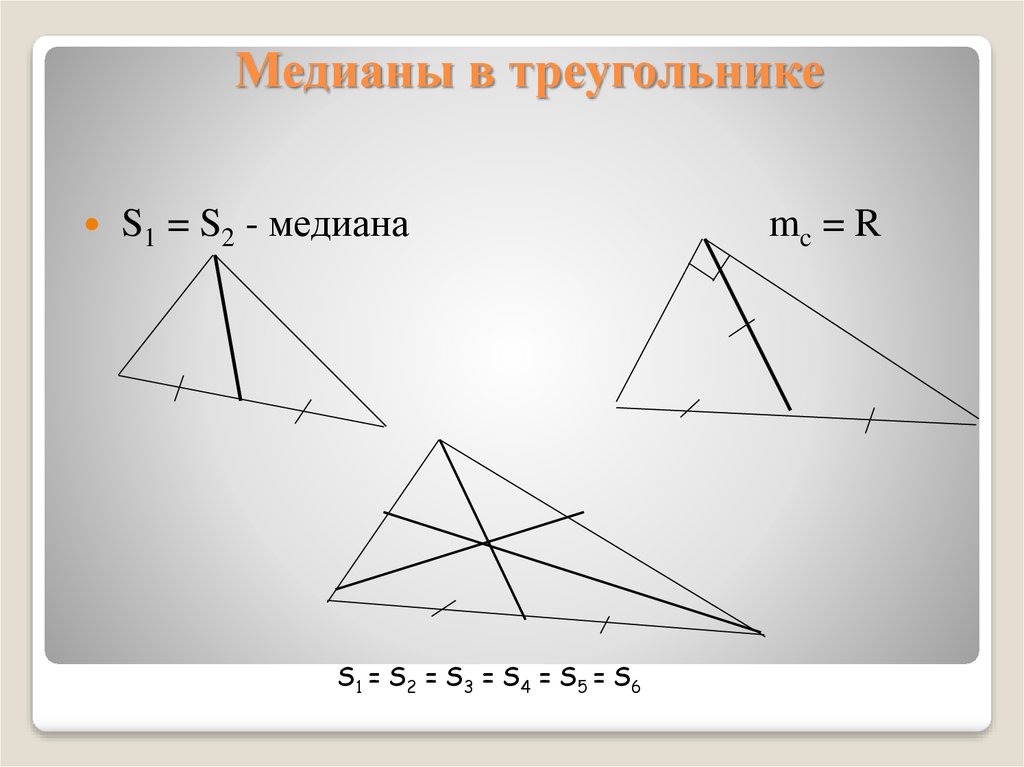
13. Медианы в треугольнике
S1 = S2 - медианаS1 = S 2 = S 3 = S 4 = S 5 = S 6
mc = R
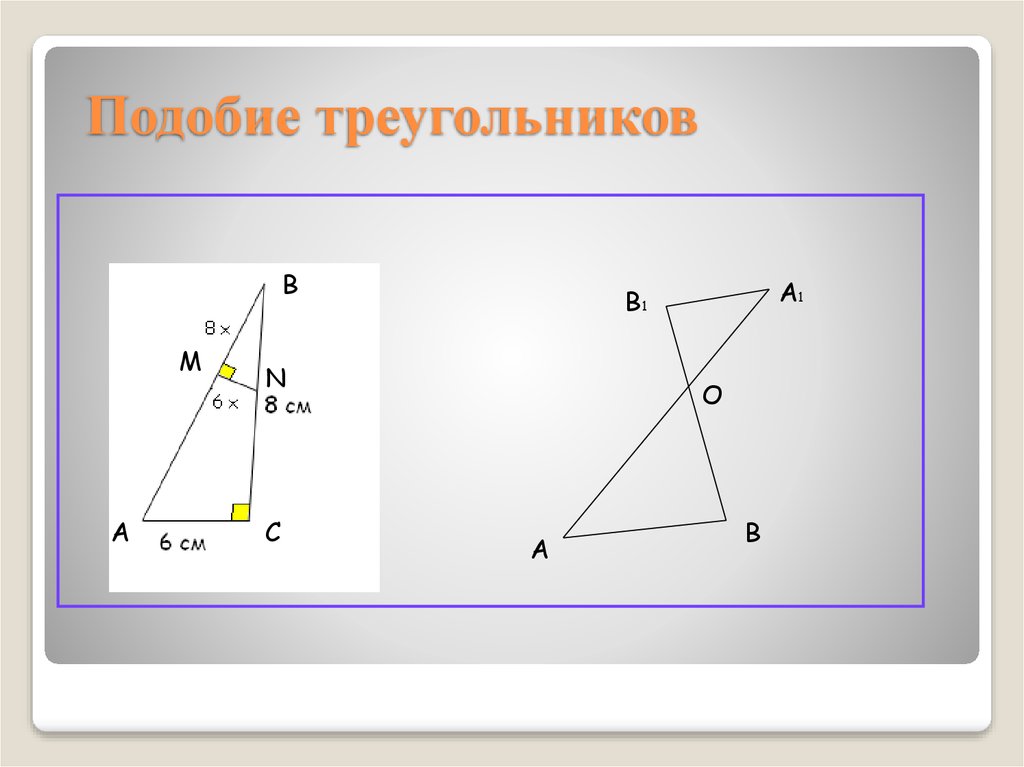
14. Подобие треугольников
BM
A
N
C
A1
B1
O
A
B
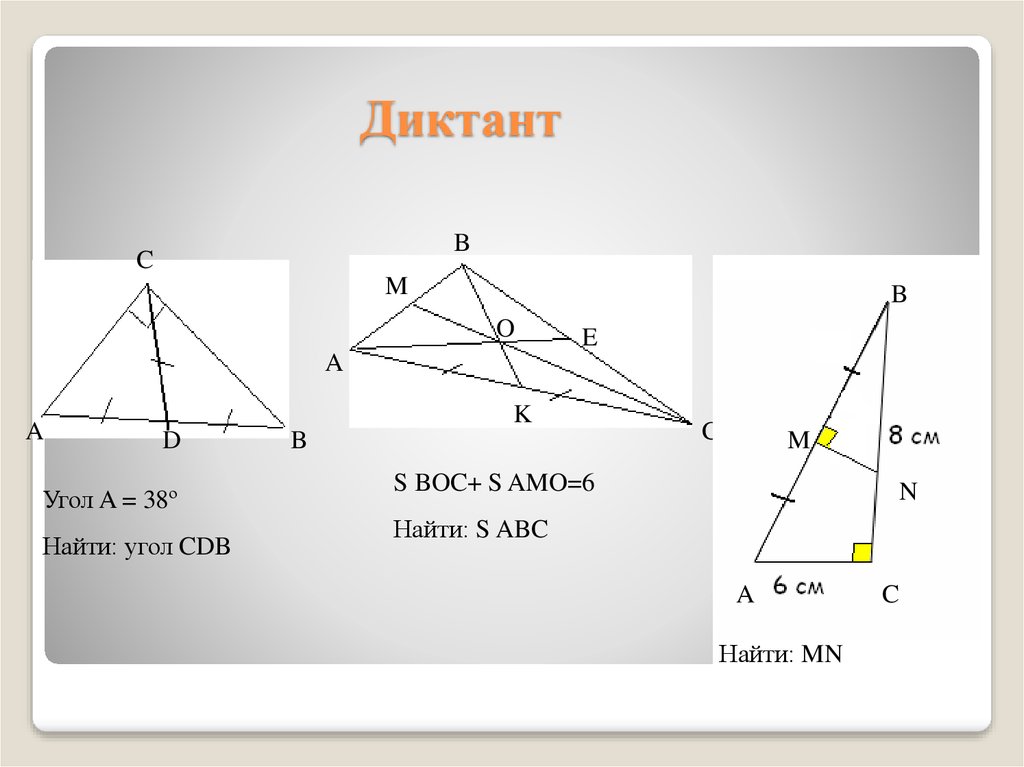
15. Диктант
BC
M
B
O
E
A
A
K
D
Угол A = 38º
Найти: угол CDB
B
C
M
S BOC+ S AMO=6
N
Найти: S ABC
A
Найти: MN
C
16.
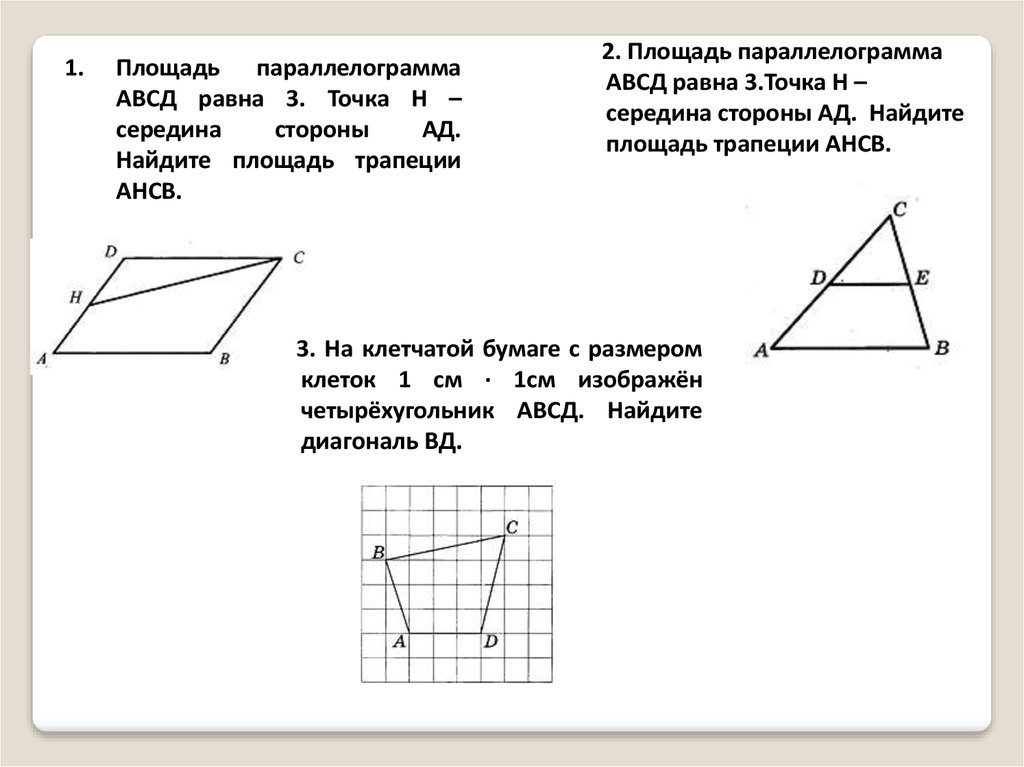
1.Площадь параллелограмма
АВСД равна 3. Точка Н –
середина
стороны
АД.
Найдите площадь трапеции
АНСВ.
2. Площадь параллелограмма
АВСД равна 3.Точка Н –
середина стороны АД. Найдите
площадь трапеции АНСВ.
3. На клетчатой бумаге с размером
клеток 1 см ∙ 1см изображён
четырёхугольник АВСД. Найдите
диагональ ВД.
17. Практикум № 1
18 PB
C
F
M
24
24
X
A
K
32
окружностей, касающихся сторон
трапеции и главной окружности.
O
L
E
Дано: В равнобокую трапецию вписана
окружность.
ВС = 36, АД = 64, r = 24
Найти: радиусы двух вписанных
1. Построение: тр-к АМК
2. 2 АВ = 100, АВ = 50 (ВС + АD = АВ + СD)
3. AF = АЕ = 32
4. АО = 40 (тр-к АОЕ)
D 5. АL = 40 - 24 = 16
6. Тр-к АОЕ подобен тр-ку АLК
х/24 = 16/32, х = 12
7. АК = 20 ( тр-к АLК – теорема Пифагора)
8. Работа с тр-ком АМК: 20, 20, 24
Найти S и r.
Главное:
1. Подобие.
2. Точка О – на биссектрисе.
3. ВС + АD = АВ + СD
18.
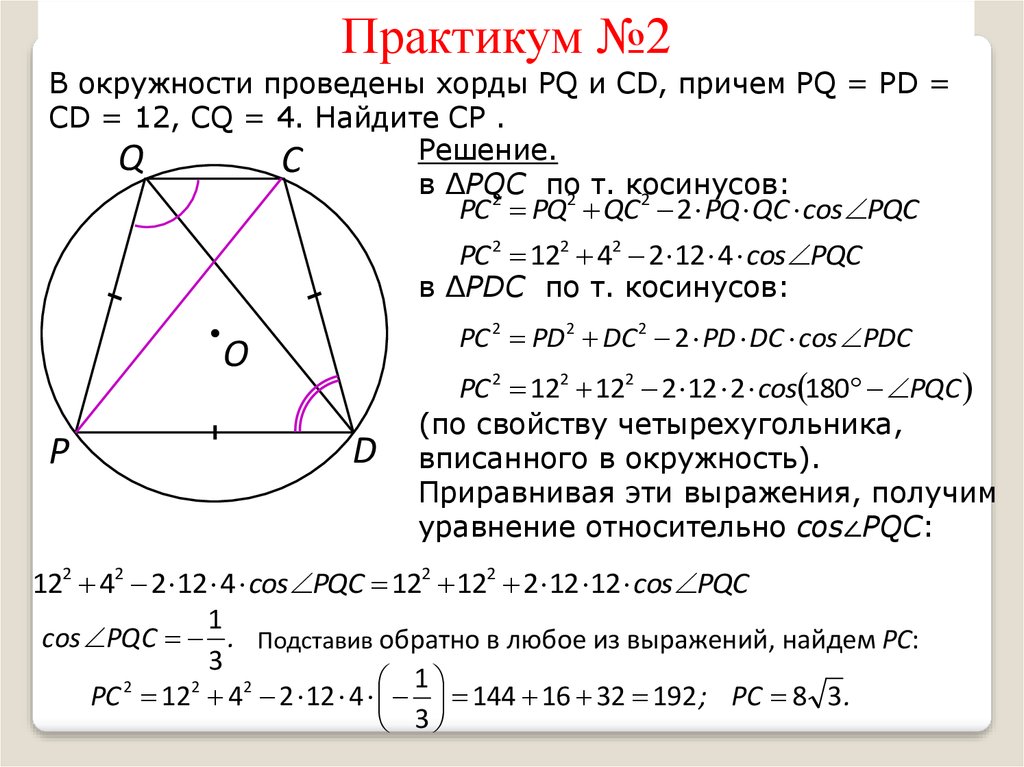
Практикум №2В окружности проведены хорды PQ и CD, причем PQ = PD =
CD = 12, CQ = 4. Найдите CP .
Решение.
Q
С
в ∆PQC
по2 т. косинусов:
2
PC PQ QC2 2 PQ QC cos PQC
PC 2 122 42 2 12 4 cos PQC
в ∆PDC по т. косинусов:
PC 2 PD 2 DC 2 2 PD DC cos PDC
O
P
D
PC 2 122 122 2 12 2 cos 180 PQC
(по свойству четырехугольника,
вписанного в окружность).
Приравнивая эти выражения, получим
уравнение относительно cos∠PQC:
122 42 2 12 4 cos PQC 122 122 2 12 12 cos PQC
1
cos PQC . Подставив обратно в любое из выражений, найдем PC:
3
1
PC 2 122 42 2 12 4 144 16 32 192 ; РС 8 3 .
3
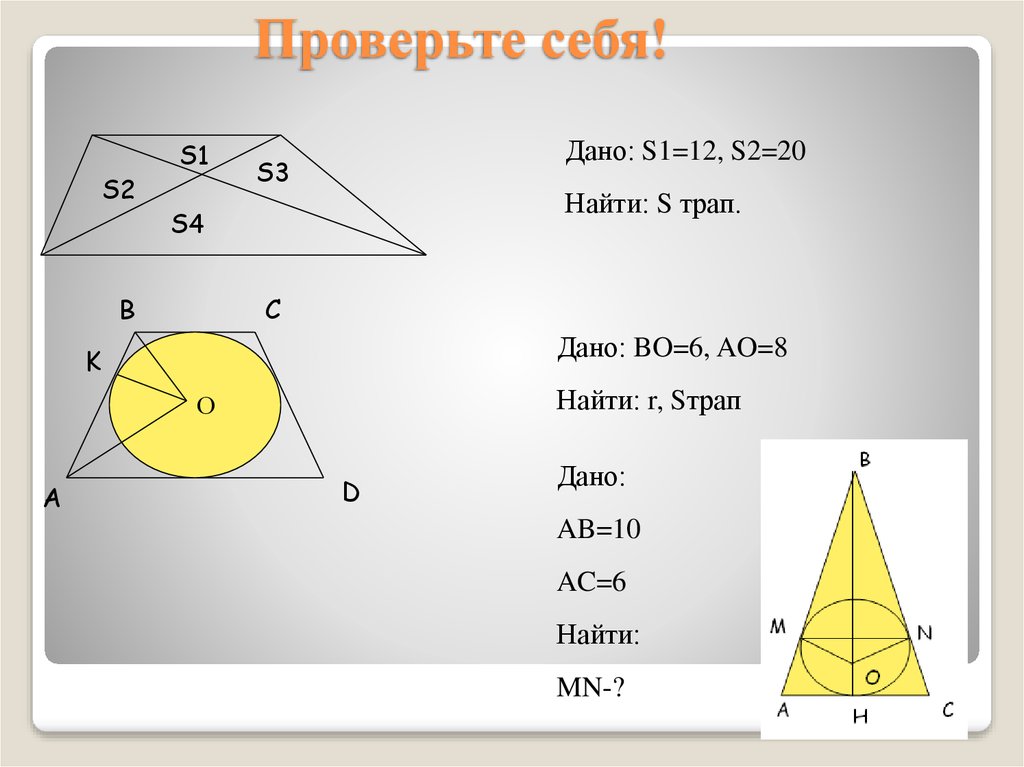
19. Проверьте себя!
S2S1
Дано: S1=12, S2=20
S3
Найти: S трап.
S4
B
C
Дано: BO=6, AO=8
K
Найти: r, Sтрап
О
A
D
Дано:
AB=10
AC=6
Найти:
MN-?
20.
Поиск решения геометрических задач1. Знание максимума теории
2. Систематическое решение задач Умения и навыки, приобретаются
только на практике.
3. Самостоятельное составление задач
4. Развитие геометрического зрения
21. Рефлексия
Продолжите, пожалуйста, фразу:В чем же величие человека или чему
учит геометрия?
22. Заключение
Уже несколько лет я работаю над темой- развитиетворческих способностей учащихся как средство
повышения качественной подготовки к ЕГЭ.
Основа математических способностей- это умение
анализировать, сравнивать, наблюдать, устанавливать
закономерность, видеть новое в стандартной
ситуации, применять известные факты в
нестандартной ситуации. Именно эти качества и
развивает геометрия.
















 mathematics
mathematics








