Плоскость в пространстве. Раздел 3

1. Раздел 3 Аналитическая геометрия Плоскость в пространстве

• Различные виды уравнений плоскости в
пространстве
• Взаимное расположение двух плоскостей в
пространстве
• Расстояние от точки до плоскости

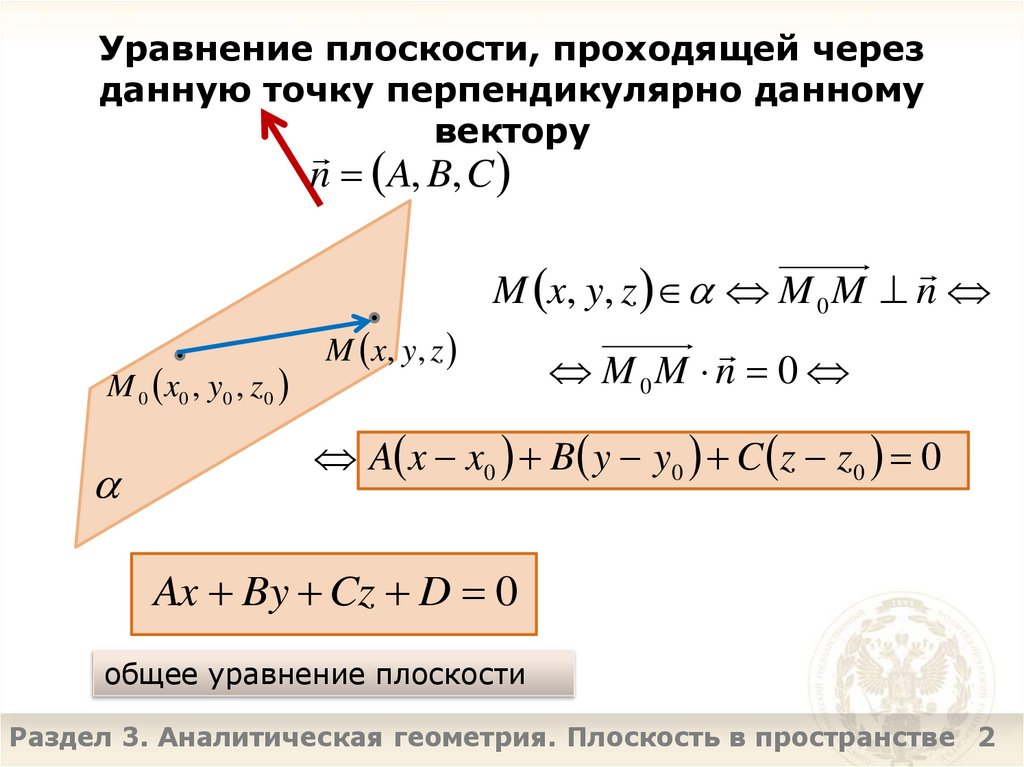
2. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

n A, B, C
M x, y, z M 0 M n
M x, y , z
M 0M n 0
M 0 x0 , y0 , z0
A x x0 B y y0 C z z0 0
Ax By Cz D 0
общее уравнение плоскости
Раздел 3. Аналитическая геометрия. Плоскость в пространстве 2

3.

Примеры: 1) Написать уравнение плоскости, проходящей через точку
M 0 1, 2, 0 перпендикулярно вектору нормали n 5, 4, 2 .
5 x 1 4 y ( 2) 2 z 0 0
5 x 4 y 2 z 13 0
2) Написать уравнение плоскости, проходящей через точку
M 0 1, 2, 3
параллельно двум направляющим векторам: a1 3, 2, 0 , a2 1, 3, 7 .
n ?
a2
M 0 1,2,3
a1
i
j k
3 2 0
n a1 a2
1 3 7
14i 21 j 11k
n 14, 21, 11
14 x ( 1) 21 y 2 11 z 3 0
14 x 21 y 11z 5 0
Раздел 3. Аналитическая геометрия. Плоскость в пространстве 3

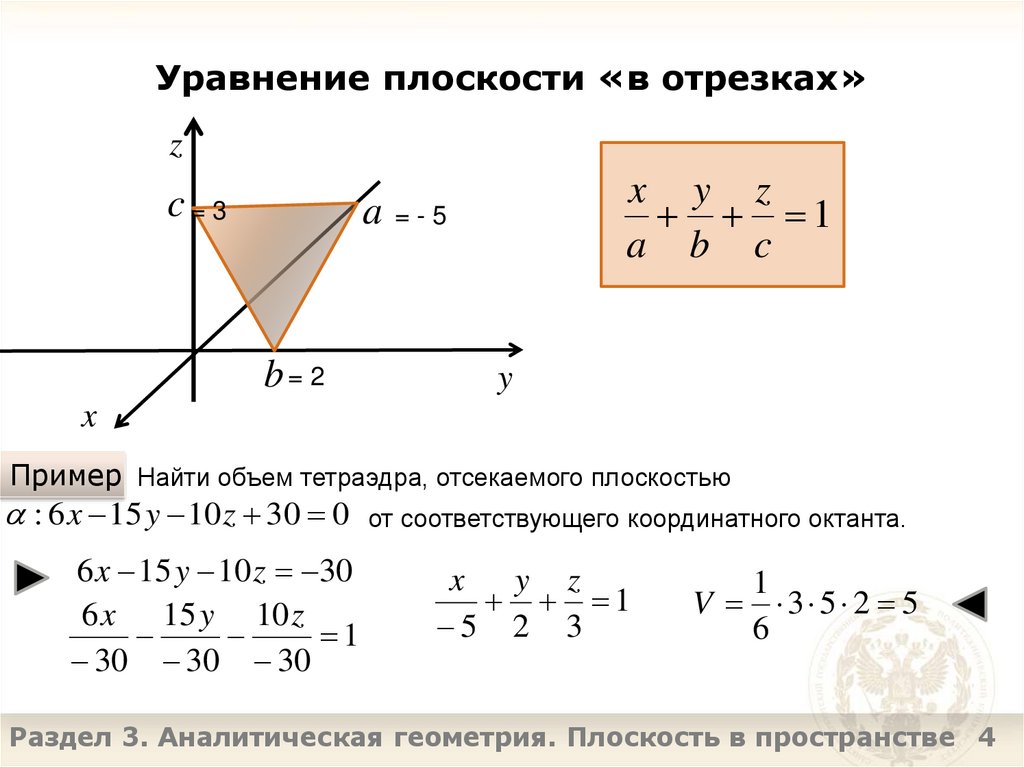
4. Уравнение плоскости «в отрезках»

z
c= 3
x y z
1
a b c
a =-5
b= 2
y
x
Пример Найти объем тетраэдра, отсекаемого плоскостью
: 6 x 15 y 10 z 30 0 от соответствующего координатного октанта.
6 x 15 y 10 z 30
6 x 15 y 10 z
1
30 30 30
x
y z
1
5 2 3
1
V 3 5 2 5
6
Раздел 3. Аналитическая геометрия. Плоскость в пространстве 4

5. Уравнение плоскости, проходящей через 3 данные точки

M 2 x2 , y 2 , z 2
M 1 x1 , y1 , z1
M x, y , z
M 3 x3 , y3 , z3
M x, y, z M 1M , M 1M 2 , M 1M 3 компланарны
x x1
M 1M M 1M 2 M 1M 3 0 x2 x1
x3 x1
y y1
y2 y1
y3 y1
z z1
z 2 z1 0
z3 z1
Раздел 3. Аналитическая геометрия. Плоскость в пространстве 5

6.

Пример Написать уравнение плоскости, проходящей через 3 данные
точки:
M 1 3, 2, 0 , M 2 3, 2, 4 , M 3 2, 5,1 .
x ( 3) y 2 z 0
3 ( 3) 2 2 4 0 0
2 ( 3) 5 2 1 0
x 3 y 2 z
6
0
4 0
5
3
1
0 4
6 4
6 0
( x 3)
( y 2)
z
0
3 1
5 1
5 3
12( x 3) 26( y 2) 18 z 0
2( x 3) 13( y 2) 3 z 0
2 x 13 y 3z 32 0
Раздел 3. Аналитическая геометрия. Плоскость в пространстве 6

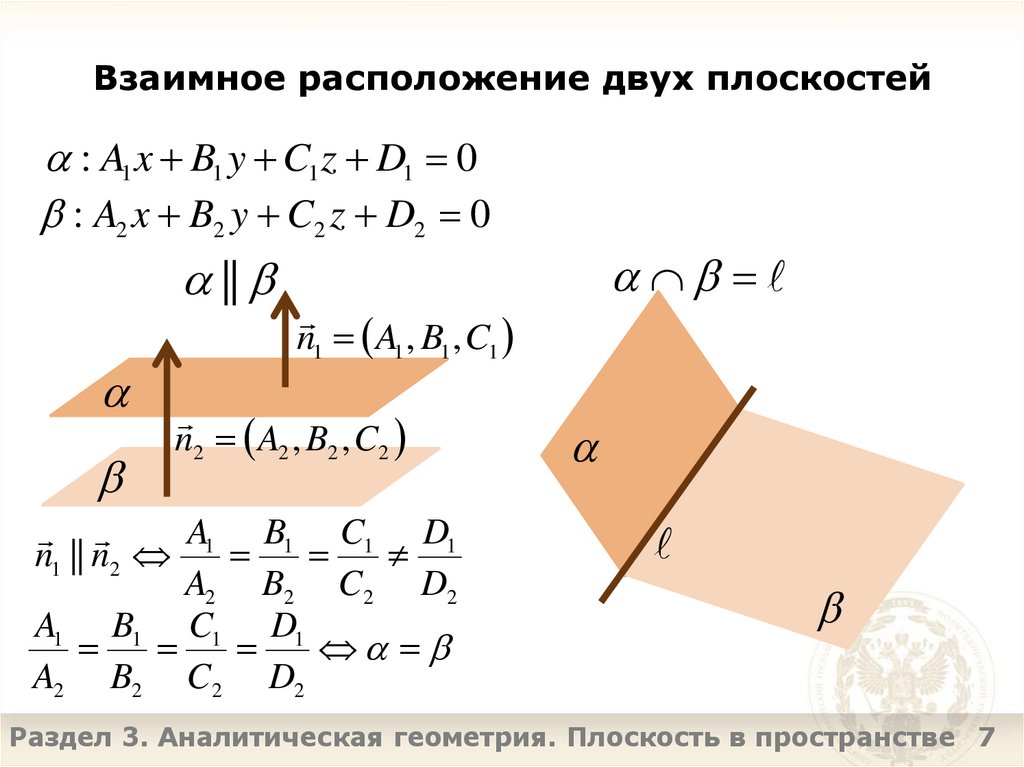
7. Взаимное расположение двух плоскостей

: A1 x B1 y C1 z D1 0
: A2 x B2 y C2 z D2 0
||
n1 A1 , B1 , C1
n2 A2 , B2 , C2
A1 B1 C1 D1
n1 || n2
A2 B2 C2 D2
A1 B1 C1 D1
A2 B2 C2 D2
Раздел 3. Аналитическая геометрия. Плоскость в пространстве 7

8. Угол между плоскостями

n A1 , B1 , C1
: A1 x B1 y C1 z D1 0
: A2 x B2 y C2 z D2 0
n A2 , B2 , C2
n
n
Угол между плоскостями – это угол между
их нормалями, если он острый или
прямой, или его дополнение до угла π.
A
A
B
B
C
C
1
2
1
2
1
2
cos cos n , n
2
2
2
2
2
2
A
B
C
A
B
C
1
1
1
2
2
2
A1 A2 B1 B2 C1C2
Раздел 3. Аналитическая геометрия. Плоскость в пространстве 8

9. Расстояние от точки до плоскости

M 1 x1 , y1 , z1
: Ax By Cz D 0
dist M 1 ,
Пример Найти расстояние от точки M 3, 2, 0
: 3x y 2 z 4 0.
dist M ,
3 ( 3) 1 2 2 0 4
32 ( 1) 2 2 2
Ax1 By1 Cz1 D
A2 B 2 C 2
до плоскости
15
14
Раздел 3. Аналитическая геометрия. Плоскость в пространстве 9

10.

Пример Выяснить взаимное расположение плоскостей. В случае если
они пересекаются, найти угол между ними. Если плоскости
параллельны, найти расстояние между ними.
: 3x y 2 z 4 0
: 6x 2 y 4z 7 0
: x 3 y 5z 7 0
n || n
n 3, 1, 2
n 6, 2, 4
n 1, 3, 5
3 1 2 4
||
6 2 4 7
6 0 2 0 4 2 7
1
M 0, 0, 2 dist , dist M ,
2
2
2
6 ( 2) 4
56
3 1 ( 1) 3 2 5
10
cos cos n , n 2
2
2
2
2
2
14 35
3 ( 1) 2 1 3 5
Раздел 3. Аналитическая геометрия. Плоскость в пространстве 10

11.

11