ЛУравнения поверхности и линии в пространстве. Плоскость в пространстве

1. Уравнения поверхности и линии в пространстве. Плоскость в пространстве

Поверхность и ее уравнение
Уравнения линии в пространстве
Уравнение плоскости, проходящей через данную
точку перпендикулярно данному вектору
Общее уравнение плоскости
Уравнение плоскости, проходящей через три
данные точки
Уравнение плоскости в отрезках
Нормальное уравнение плоскости
Угол между двумя плоскостями
Расстояние от точки до плоскости

2. Поверхность и ее уравнение

Определение

3.

Поверхность и ее уравнение

4. Поверхность и ее уравнение

5. Поверхность и ее уравнение

6. Уравнения линии в пространстве

7. Уравнения линии в пространстве

8. Уравнения линии в пространстве

9. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

10. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

11. Общее уравнение плоскости

Общее уравнение плоскости

12. Общее уравнение плоскости

Общее уравнение плоскости называется полным, если все
коэффициенты А; B; C; D отличны от нуля.
В противном случае уравнение называется неполным.

13. Общее уравнение плоскости

Виды неполных уравнений:
1) D 0;
2) A 0;
Ax By Cz 0 Плоскость проходит через точку О.
By Cz D 0 ll (OX )
z
3) B 0;
Ax Cz D 0
ll (OY )
4) C 0;
Ax By D 0
ll (OZ )
5) A 0; B 0
Cz D 0 ll ( XOY )
6) B 0; C 0 Ax D 0 ll (YOZ )
7) A 0; C 0
0
By D 0 ll ( XOZ ) x
8) B 0; C 0; D 0
Ax 0 x 0
9) A 0; C 0; D 0
By 0 y 0
Cz 0 z 0
10) A 0; B 0; D 0
(YOZ )
( XOZ )
( XOY )
y

14. Уравнение плоскости, проходящей через три данные точки

15. Уравнение плоскости, проходящей через три данные точки

16. Уравнение плоскости, проходящей через три данные точки

Пусть точки М1(х1 ; у1 ; z1 ), М2(х2 ; у2 ; z2 ) и М3(х3 ; у3 ; z3 ) не лежат
на одной прямой.
Тогда векторы: M1M 2 x2 x1; y2 y1; z2 z1
и
M1M 3 x3 x1; y3 y1; z3 z1
Точка М(х ; у ; z ) лежит в
одной плоскости с точками
М1 , М2 и М3 только в том
случае, если векторы:
не коллинеарны.
М3
М1
М
М2
M1M2 ; M1M3 и M1M x x1; y y1; z z1
Уравнение плоскости,
проходящей через 3 точки
x x1
x 2 x1
x3 x1
y y1
y 2 y1
y 3 y1
компланарны.
z z1
z2 z1 0
z3 z1

17. Уравнение плоскости, проходящей через три данные точки

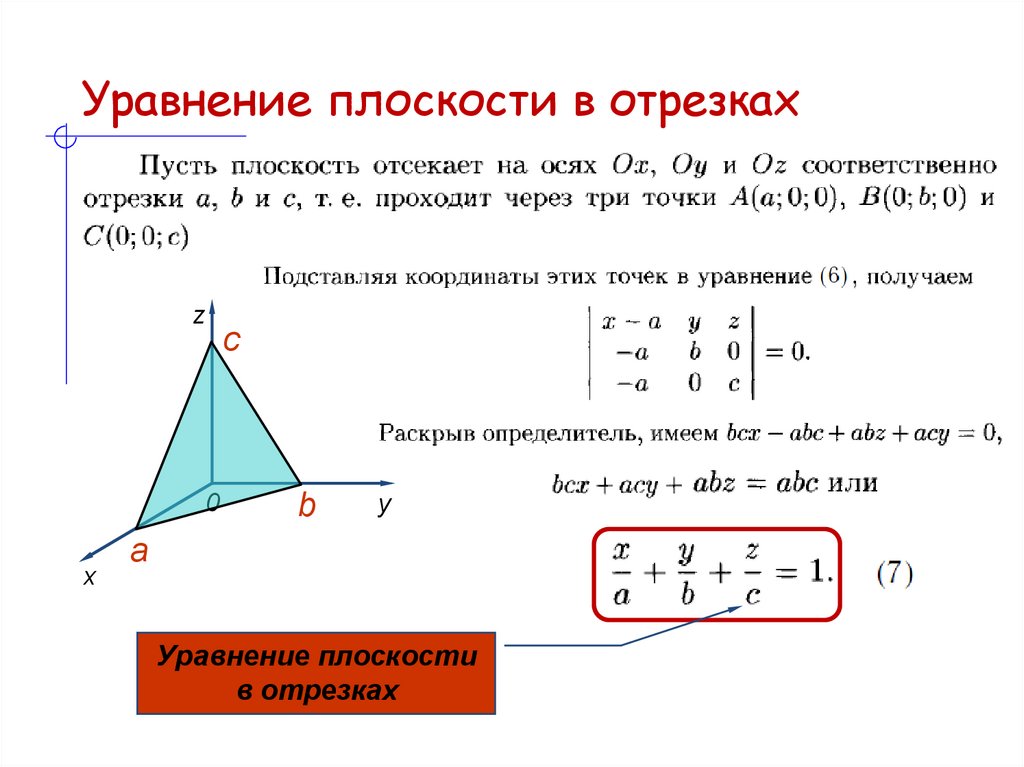
18. Уравнение плоскости в отрезках

z
с
0
x
b
y
a
Уравнение плоскости
в отрезках

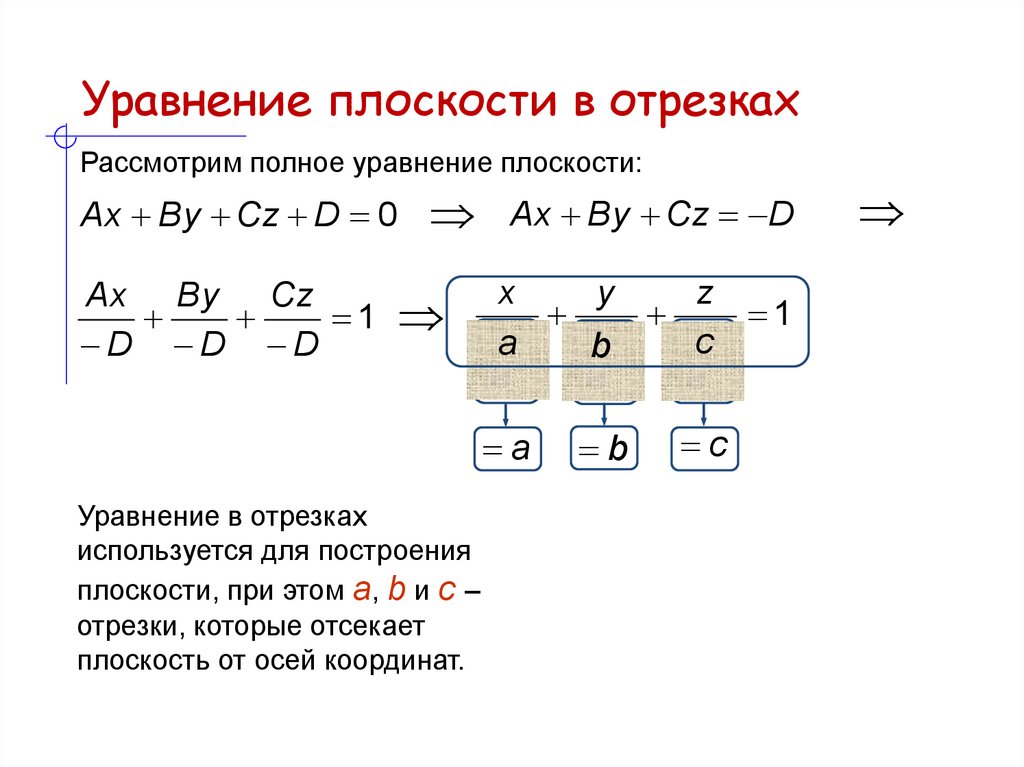
19. Уравнение плоскости в отрезках

Рассмотрим полное уравнение плоскости:
Ax By Cz D 0
Ax By Cz
1
D D D
Ax By Cz D
x
y
z
1
aD bD cD
A
B
C
a
Уравнение в отрезках
используется для построения
плоскости, при этом a, b и с –
отрезки, которые отсекает
плоскость от осей координат.
b
c

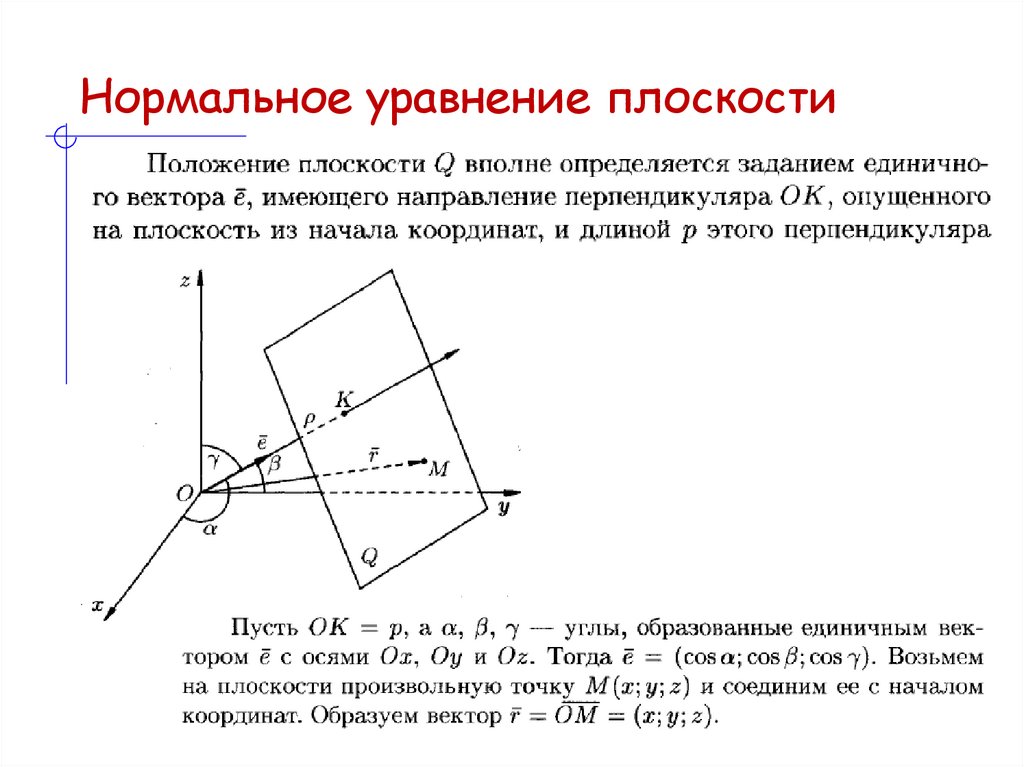
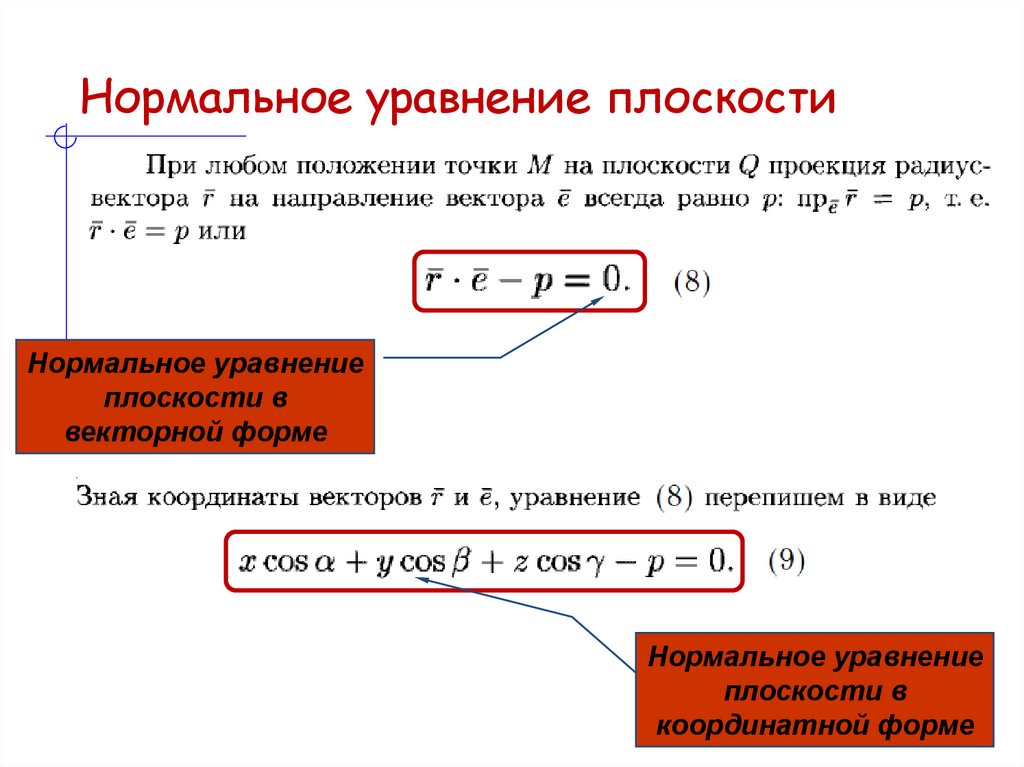
20. Нормальное уравнение плоскости

21. Нормальное уравнение плоскости

Нормальное уравнение
плоскости в
векторной форме
Нормальное уравнение
плоскости в
координатной форме

22. Нормальное уравнение плоскости

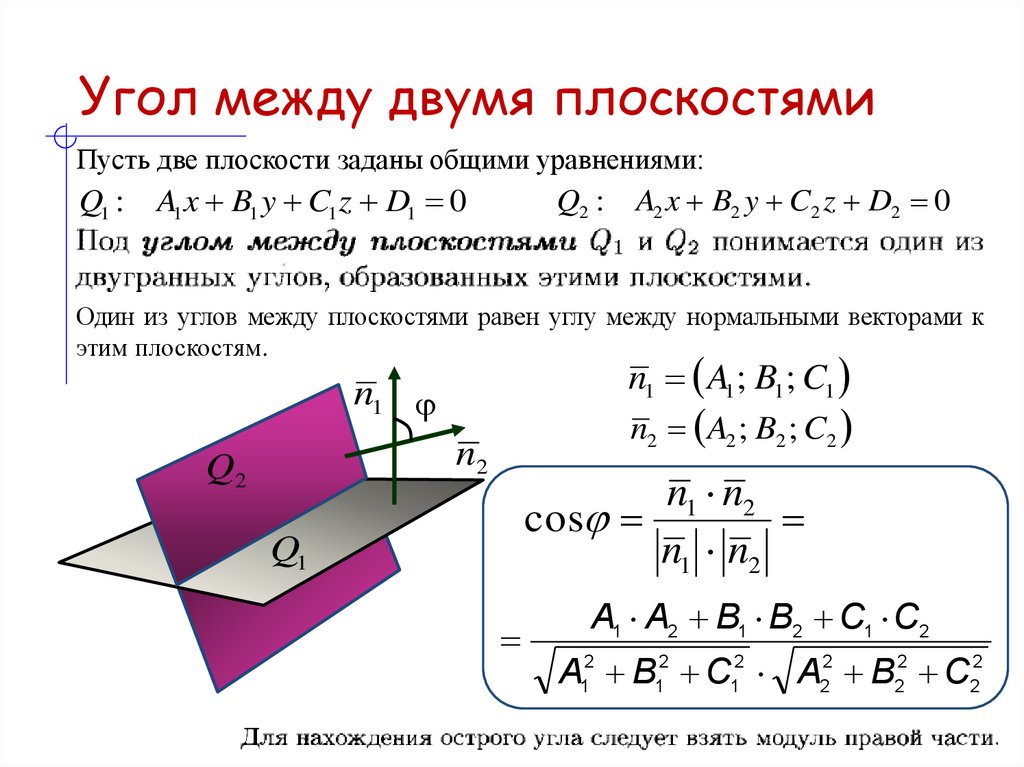
23. Угол между двумя плоскостями

Пусть две плоскости заданы общими уравнениями:
Q1 :
A1 x B1 y C1 z D1 0
Q2 :
A2 x B2 y C2 z D2 0
Один из углов между плоскостями равен углу между нормальными векторами к
этим плоскостям.
n1 A1; B1; C1
n1
n2 A2 ; B2 ; C2
n2
Q2
n1 n2
cos
n1 n2
Q1
A1 A2 B1 B2 C1 C2
A12 B12 C12 A22 B22 C22

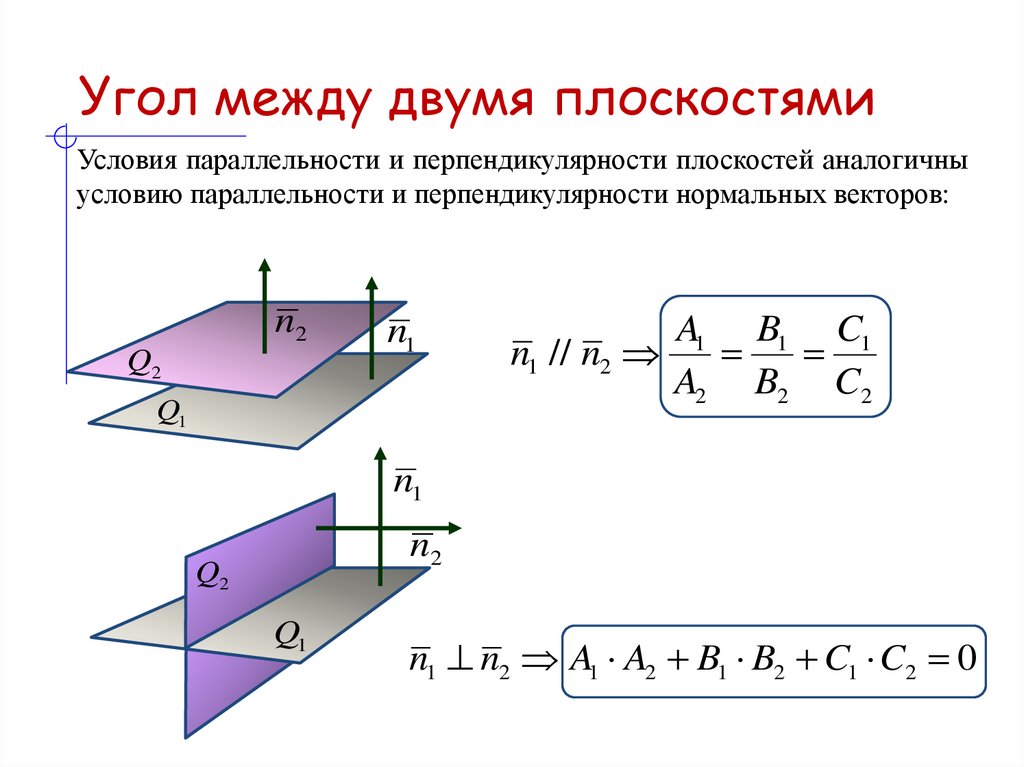
24. Угол между двумя плоскостями

Условия параллельности и перпендикулярности плоскостей аналогичны
условию параллельности и перпендикулярности нормальных векторов:
n2
Q2
n1
Q1
A1 B1 C1
n1 // n2
A2 B2 C2
n1
n2
Q2
Q1
n1 n2 A1 A2 B1 B2 C1 C2 0

25.

Расстояние от точки до плоскости

26. Расстояние от точки до плоскости

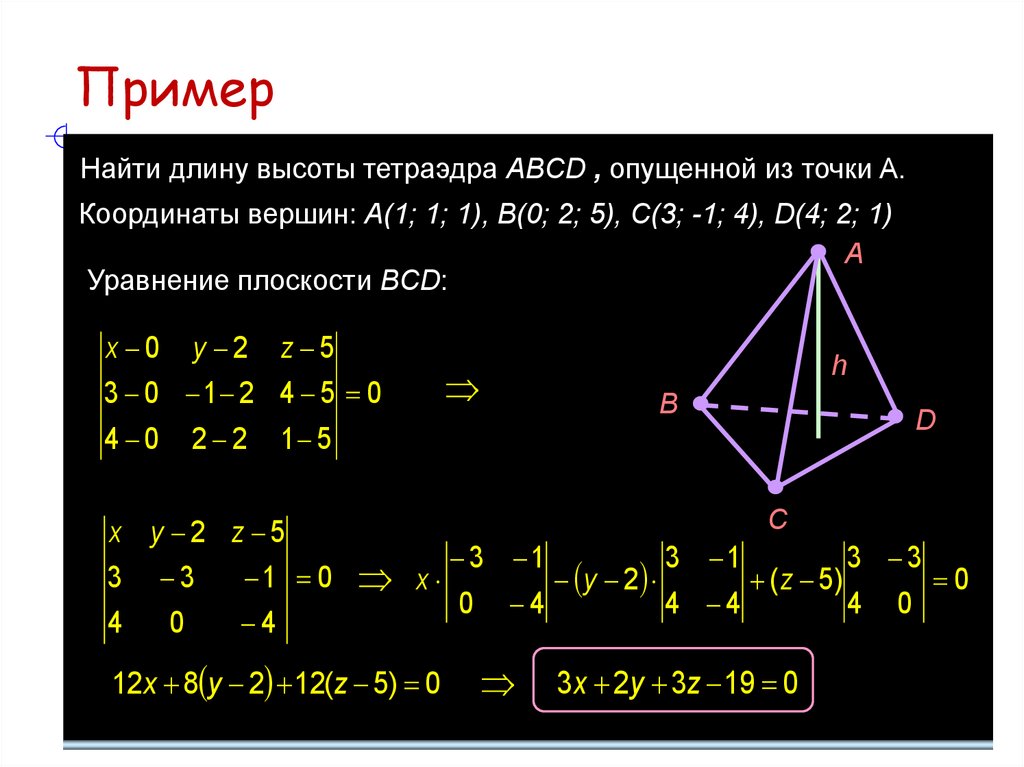
27. Пример

Найти длину высоты тетраэдра ABCD , опущенной из точки A.
Координаты вершин: A(1; 1; 1), B(0; 2; 5), C(3; -1; 4), D(4; 2; 1)
A
Уравнение плоскости BCD:
x 0 y 2 z 5
3 0 1 2 4 5 0
4 0 2 2 1 5
x y 2 z 5
3 3
1 0
4
0
4
h
B
D
С
3 1
3 1
3 3
x
y 2
( z 5)
0
0 4
4 4
4 0
12x 8 y 2 12(z 5) 0
3 x 2y 3z 19 0

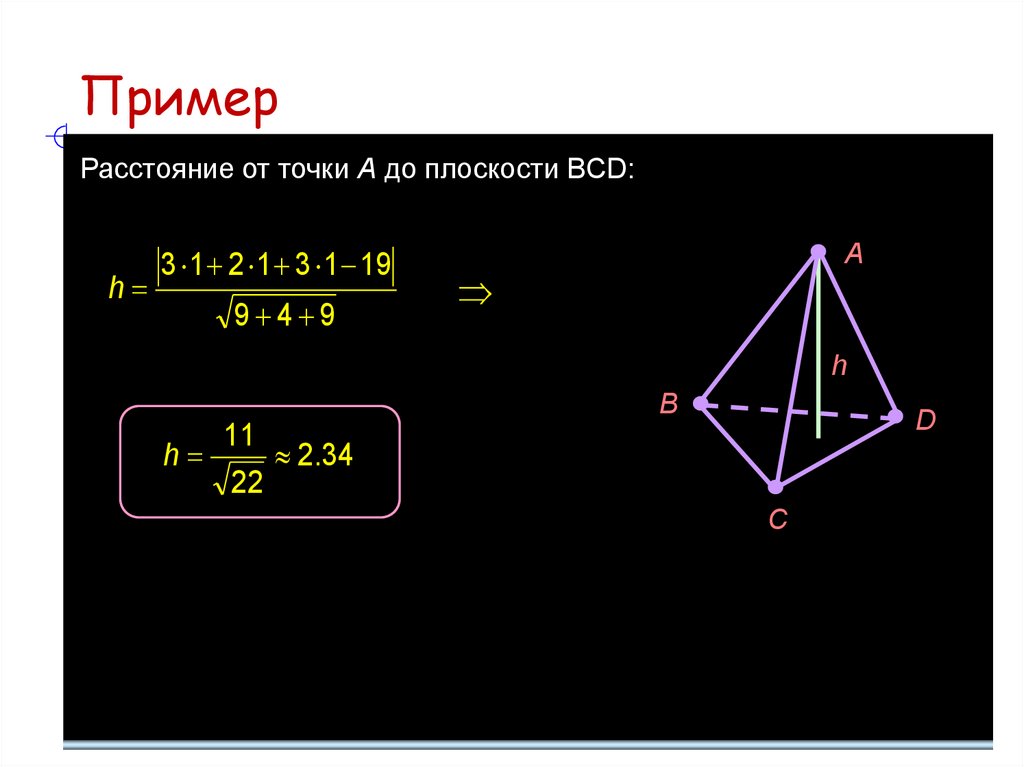
28. Пример

Расстояние от точки A до плоскости BCD:
h
3 1 2 1 3 1 19
9 4 9
A
h
B
D
11
h
2.34
22
С