Молекулярная физика. Основы термодинамики

1. Физика Молекулярная физика

Дальневосточный федеральный университет
Физика
Молекулярная физика
Основы термодинамики
Осьмушко Иван Сергеевич

2. Внутренняя энергия и степени свободы

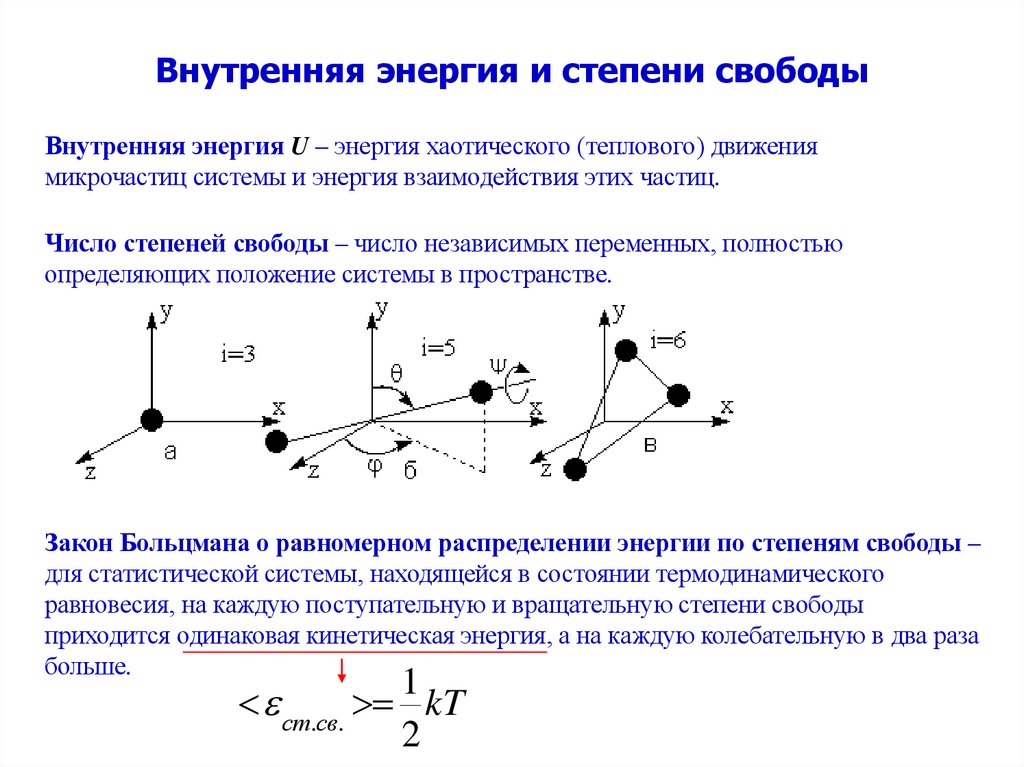
Внутренняя энергия U – энергия хаотического (теплового) движения
микрочастиц системы и энергия взаимодействия этих частиц.
Число степеней свободы – число независимых переменных, полностью
определяющих положение системы в пространстве.
Закон Больцмана о равномерном распределении энергии по степеням свободы –
для статистической системы, находящейся в состоянии термодинамического
равновесия, на каждую поступательную и вращательную степени свободы
приходится одинаковая кинетическая энергия, а на каждую колебательную в два раза
больше.
1
ст.св. kT
2

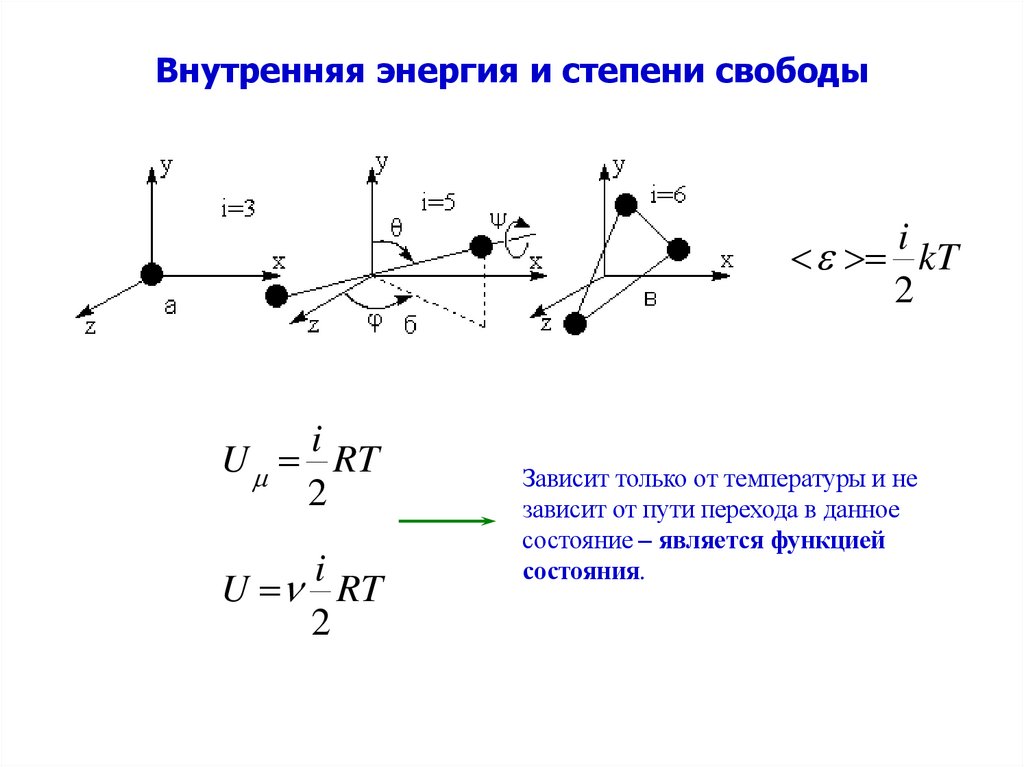
3. Внутренняя энергия и степени свободы

i
kT
2
i
U RT
2
i
U RT
2
Зависит только от температуры и не
зависит от пути перехода в данное
состояние – является функцией
состояния.

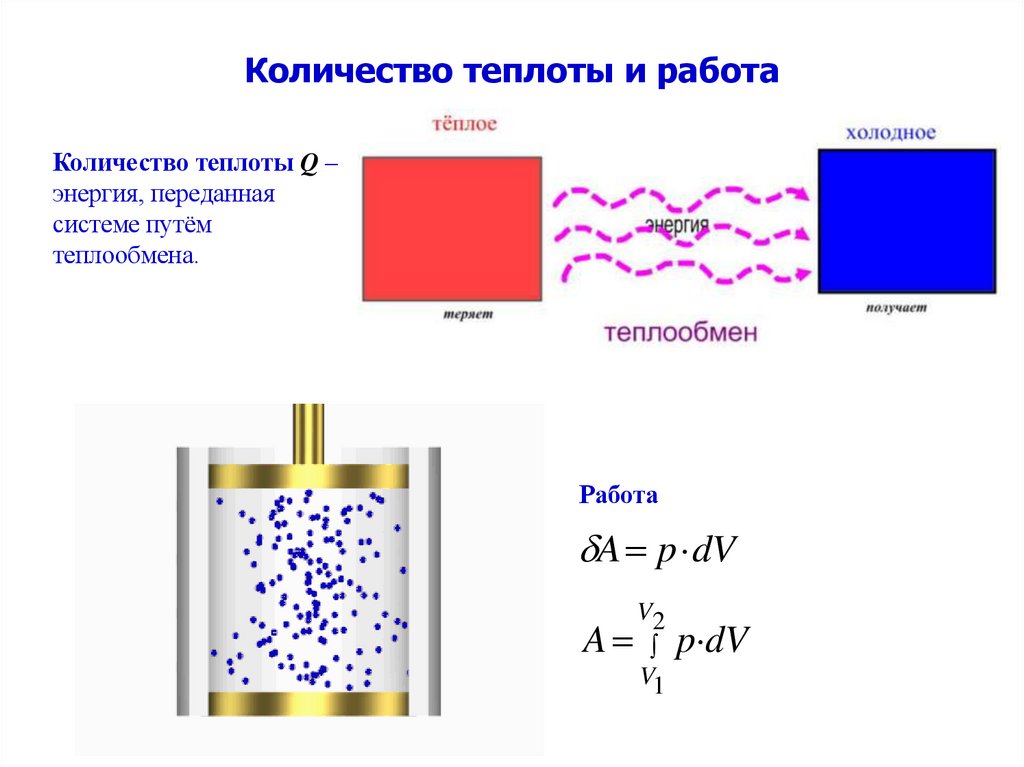
4. Количество теплоты и работа

Количество теплоты Q –
энергия, переданная
системе путём
теплообмена.
Работа
A p dV
V2
A p dV
V1

5. Первое начало термодинамики

Q U A
Теплота, сообщаемая системе, расходуется на изменение внутренней
энергии этой системы и на совершение ею работы против внешних сил.
U Q A
Внутренняя энергия системы может быть изменена посредством сообщения
этой системе теплоты или совершением работы над этой системой.
Принцип эквивалентности теплоты и работы
Q dU A
U 0,
Теплота и работа –
функции процесса.
Невозможен вечный
двигатель первого рода.
A Q

6. Теплоёмкость, уравнение Майера

c
Q
m dT
Q
C
dT
CV
dU
dT
iR
CV
2
(i 2)R
Cp
2
Удельная теплоёмкость
C c
Молярная теплоёмкость
Дж
[c]
кг К
Дж
[C ]
моль К
Уравнение Майера
C p CV R
R – работа, совершаемая одним молем идеального
газа при изобарическом нагревании на один кельвин.
Механический эквивалент теплоты: 1 кал = 4,19 Дж.

7.

Изохорный процесс V const
Диаграмма этого процесса (изохора) в координатах
p, V изображается прямой, параллельной оси ординат
(см. рис.), где процесс 2-1 есть изохорное нагревание, а
2-3 - изохорное охлаждение. При изохорном процессе
газ не совершает работы над внешними телами, т.е.
A pdV 0
Из первого начала термодинамики для изохорного
процесса следует, что вся теплота, сообщаемая газу,
идет на увеличение его внутренней энергии:
Q dU
dU m CV dT
Тогда для произвольной массы газа
получим
Q dU
m
CV dT

8.

Изобарный процесс p const
Диаграмма этого процесса (изобара) в координатах p, V
изображается прямой, параллельной оси V
При изобарном процессе работа газа при
увеличении объема от V1 до V2 равна
V2
A pdV p(V2 V1 )
V1
и определяется площадью заштрихованного прямоугольника (см. рис.). Если использовать уравнение
Клапейрона-Менделеева
для
выбранных
двух
состояний, то
pV1
m
RT1 и pV2
m
RT2 , откуда
m R
V2 V1
(T2 T1 )
p

9.

Тогда выражение для работы изобарного расширения
примет вид
m R
A
(T2 T1 )
Из этого выражения вытекает физический смысл
молярной газовой постоянной R
Если T2 T1 1 , то для 1 моль газа
R A , т.е.
R численно равна работе изобарного расширения 1
моль идеального газа при нагревании его на 1 К.
В изобарном процессе при сообщении газу массой m
количества теплоты Q
m
C p dT , его внутренняя
m
энергия возрастает на величину dU CV dT
При этом газ
выражением
совершит
A
m R
dT
работу,
определяемую

10.

Изотермический процесс T const
Изотермический процесс описывается законом БойляpV const
Мариотта:
Диаграмма этого процесса (изотерма) в координатах
p, V представляет собой гиперболу, расположенную на
диаграмме тем выше, чем выше температура, при
которой происходит процесс.
найдем работу изотермического расширения газа:
V2
V2
V2 m
p1
dV m
A pdV RT
RT ln
RT ln
V
V1
p2
V1
V1
m
Так как при T const внутренняя энергия идеального
газа не изменяется:
dU
m
CV dT 0

11.

то из первого начала термодинамики следует, что для
изотермического процесса
Q A
т.е. все количество теплоты, сообщаемое газу,
расходуется на совершение им работы против
внешних сил:
V2 m
p1
A Q RT ln
RT ln
V1
p2
m
Следовательно, для того чтобы при расширении газа
температура не понижалась, к газу в течение
изотермического процесса необходимо подводить
количество теплоты, эквивалентное внешней работе
расширения.

12.

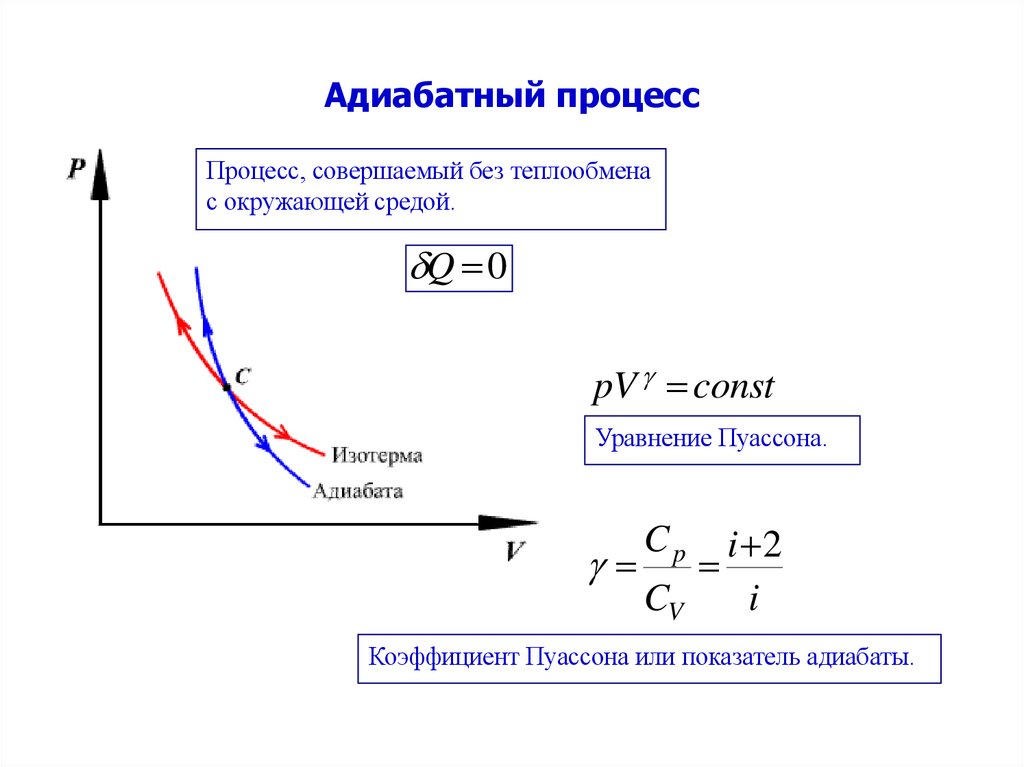
13. Адиабатный процесс

Процесс, совершаемый без теплообмена
с окружающей средой.
Q 0
pV const
Уравнение Пуассона.
i 2
CV
i
Cp
Коэффициент Пуассона или показатель адиабаты.

14.

Адиабатный процесс
Адиабатическим называется процесс, при котором
отсутствует теплообмен ( Q 0)между системой и
окружающей средой. К адиабатическим процессам
можно отнести все быстропротекающие процессы.
Например, процесс распространения звука в среде, так
как скорость распространения звуковой волны
настолько велика, что обмен энергией между волной и
средой произойти не успевает. Адиабатические
процессы применяются в ДВС (расширение и сжатие
горючей смеси в цилиндрах), в холодильных
установках и т.д.
Из
первого
начала
термодинамики
для
адиабатического процесса следует, что
A dU
т.е. внешняя работа совершается за счет изменения
внутренней энергии системы.

15.

pdV
m
CV dT
Продифференцировав уравнение состояния
m
идеального газа pV RT получим
для
pdV Vdp
m
RdT
Исключим температуру T
C p CV
pdV Vpd
R
pdV
CV
CV
Разделив переменные и учитывая, что C p / CV ,
найдем
dp
dV
p
V

16.

Интегрируя это уравнение в пределах от p до p 2 и
1
соответственно от V1 до V2 , а затем потенцируя,
придем к выражению
p2 V1
p1 V2
или
p1V1 p 2V2
Так как состояния 1 и 2 выбраны произвольно, то
можно записать
pV const
Полученное
выражение
адиабатического
процесса,
уравнением Пуассона.
есть
уравнение
называемое
также

17.

Для перехода к переменным
p, T или T , V исключим
с помощью уравнения Клапейрона-Менделеева
соответственно давление или объем:
1
TV
const
T p1 const
В этих уравнениях безразмерная величина
(i 2)
CV cV
i
Cp
cp
называется
показателем
коэффициентом Пуассона).
адиабаты
(или

18.

Для одноатомных газов ( Ne, He и др.), достаточно хорошо
удовлетворяющих условию идеальности, i 3 и 1,67
Для двухатомных газов ( H 2 , N 2 , O2 и др.), i 5
и 1,4
Значения , хорошо подтверждаются
экспериментом.
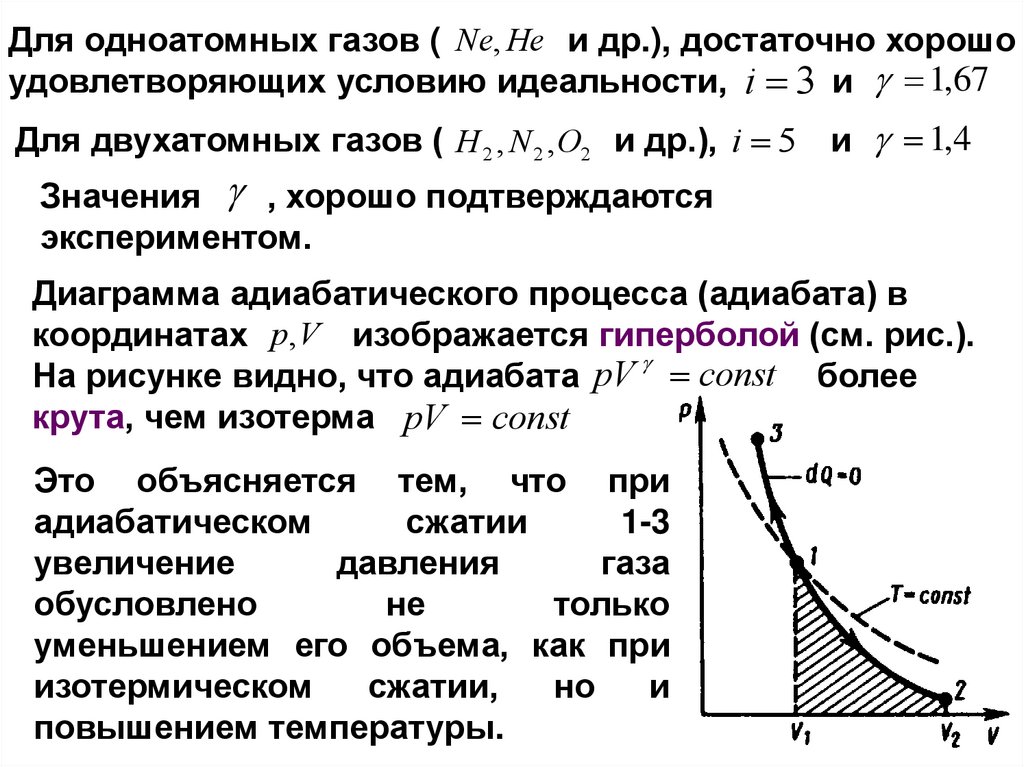
Диаграмма адиабатического процесса (адиабата) в
координатах p, V изображается гиперболой (см. рис.).
На рисунке видно, что адиабата pV const более
крута, чем изотерма pV const
Это объясняется тем, что при
адиабатическом
сжатии
1-3
увеличение
давления
газа
обусловлено
не
только
уменьшением его объема, как при
изотермическом
сжатии,
но
и
повышением температуры.

19.

Вычислим работу, совершаемую газом в адиабатическом процессе. Запишем первое начало в виде
A
m
CV dT
Если газ адиабатически расширяется от объема V1 до V2
то его температура уменьшается от T1 до T 2 и работа
расширения идеального газа
A
m
T2
CV dT
T1
m
CV (T1 T2 )
Применяя те же приемы, что и ранее, выражение для
работы при адиабатическом расширении можно
преобразовать к виду
1
1
V1
V1
p1V1
RT1 m
1
1
A
1 V2 1 V2

20.

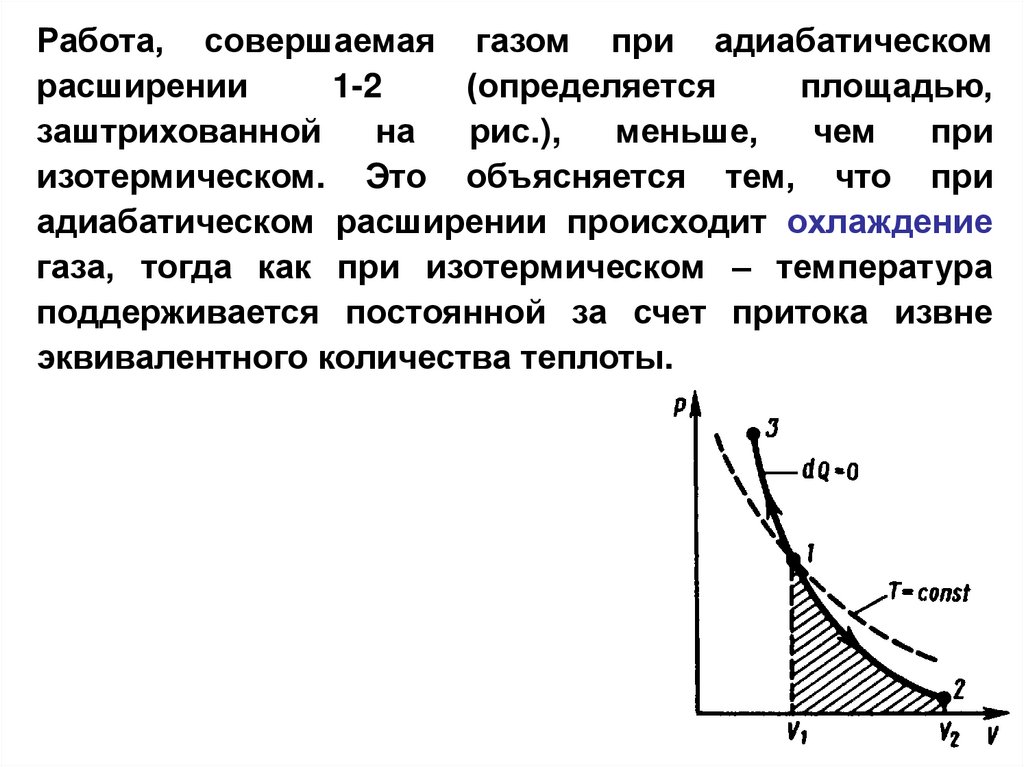
Работа, совершаемая газом при адиабатическом
расширении
1-2
(определяется
площадью,
заштрихованной
на
рис.),
меньше,
чем
при
изотермическом. Это объясняется тем, что при
адиабатическом расширении происходит охлаждение
газа, тогда как при изотермическом – температура
поддерживается постоянной за счет притока извне
эквивалентного количества теплоты.

21.

Политропные процессы
Рассмотренные
изохорный,
изобарный,
изотермический и адиабатический процессы имеют
общую особенность - они происходят при постоянной
теплоемкости.
В
первых
двух
процессах
теплоемкости
соответственно равны CV и C p ,
в изотермическом процессе ( dT 0
равна
) теплоемкость
в адиабатическом ( Q 0 ) теплоемкость равна нулю.
Процесс,
в
котором
теплоемкость
постоянной, называется политропным.
остается

22.

23.

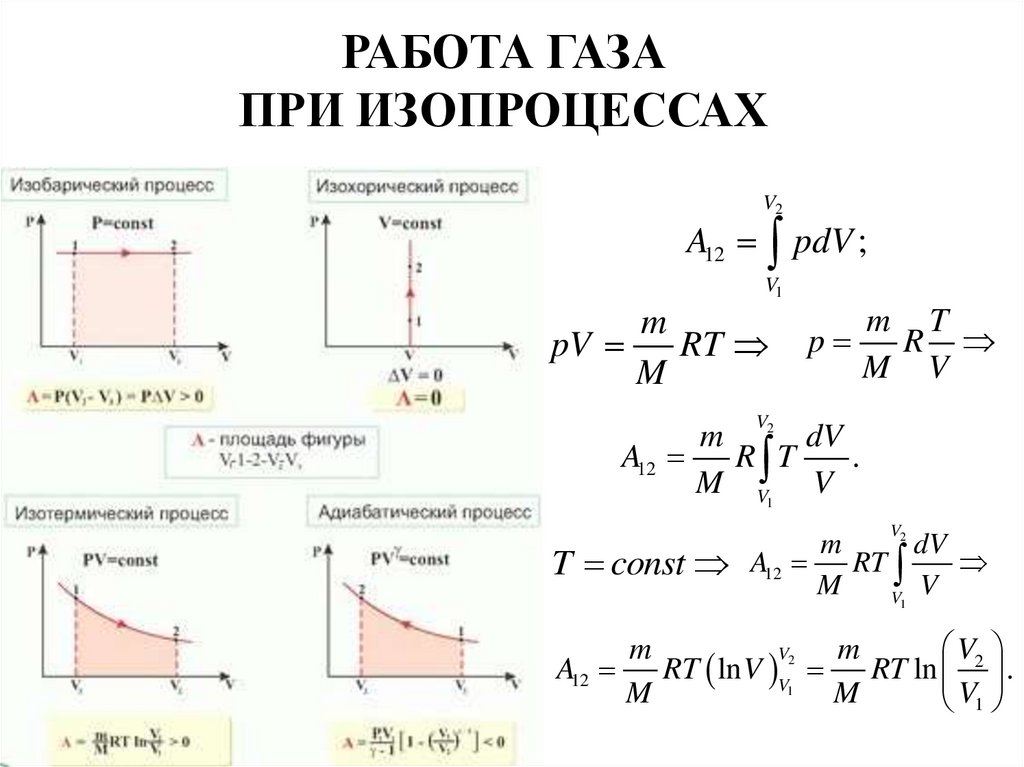
24. РАБОТА ГАЗА ПРИ ИЗОПРОЦЕССАХ

V2
A12 pdV ;
V1
m
pV
RT
M
p
m T
R
M V
V
m 2 dV
A12
R T
.
M V1 V
V
2
m
dV
T const A12 RT
M
V
V1
V2
m
m
V2
A12
RT ln V V
RT ln .
1
M
M
V1