Similar presentations:
Вычислите. Применение тригонометрических тождеств
1.
Вычислите2.
Цель: проверить умение учащихся (студентов):1.Применять тригонометрические тождества сумм и
разностей (sinA−sinB\sin A - \sin BsinA−sinB,
cosA+cosB\cos A + \cos BcosA+cosB и пр.).
2.Рационально упрощать выражения, используя базовые
значения sin\sinsin и cos\coscos стандартных углов
(π/6\pi/6π/6, π/3\pi/3π/3, π/5\pi/5π/5 и т. д.).
3.Выявлять итоговое числовое значение выражения
(включая специальные случаи, когда оно обращается
в ноль).
4.Лаконично и логично представлять решение, указывая
каждое тригонометрическое преобразование.
3.
Определение критериев (пример)Выделим 5 критериев, максимально по 2 балла за каждый (итого 10 баллов):
1.Понимание задачи и формулировка подхода
1. Оценка корректности интерпретации выражения и осознанного выбора тригонометрических
формул разности/суммы.
2.Применение тригонометрических тождеств
1. Проверка знания и корректного использования формул sinA−sinB\sin A - \sin
BsinA−sinB, cosA+cosB\cos A + \cos BcosA+cosB, а также значений
sin(π/6)\sin(\pi/6)sin(π/6), cos(π/3)\cos(\pi/3)cos(π/3) и т.п.
3.Алгебраическая аккуратность
1. Правильное выполнение вычислений без арифметических ошибок, внимательное обращение
с дробями и π\piπ.
4.Итоговый результат
1. Проверка, что учащийся дошёл до верного итогового значения (здесь оно равно 0).
Умение проверять результат.
5.Структура и ясность записи
1. Оформление решения по шагам, использование поясняющих комментариев, аккуратное
изложение.
4.
Выбор приёмов и формы оценивания• Формы:
• Индивидуальная письменная работа или устный разбор у
доски с комментариями.
• Тестовый формат с несколькими аналогичными заданиями на
упрощение тригонометрических выражений.
• Приёмы:
• Использовать список тригонометрических формулсокращений, чтобы ученик смог применить их
целенаправленно (например, выдаётся «шпаргалка» с
основными тождествами).
• Предварительная работа с типовыми углами и их
синусами/косинусами.
• Возможность самопроверки: вычислить приближённое
значение выражения на калькуляторе (до задания и после
решения), чтобы убедиться в правильности.
5.
Для тренировки предлагаеманалогичные выражения, чтобы
учащиеся отработали разные
комбинации:
6.
1. Понимание задачи и формулировка подхода1.
2.
3.
2 балла: явно указано, какие тождества планируется использовать (sinA−sinB\sin A - \sin BsinA−sinB, cosA+cosB\cos A + \cos
BcosA+cosB и т.д.), осознанно выбрана схема решения.
1 балл: подход в целом верный, но сформулирован кратко или упущены пояснения.
0 баллов: решение идёт «вслепую», без указания, какие именно формулы следует применять.
2. Применение тригонометрических тождеств
1.
2.
3.
2 балла: все формулы применены корректно, без путаницы в знаках и аргументах.
1 балл: допущены небольшие неточности (опечатки, знаки), но решение можно довести до верного при небольших исправлениях.
0 баллов: грубые ошибки (неверные формулы, неправильная замена).
3. Алгебраическая аккуратность
1.
2.
3.
2 балла: никакой путаницы с дробями, π\piπ и числовыми значениями тригонометрических функций, всё последовательно.
1 балл: есть арифметические огрехи, но итоговый результат всё же можно восстановить.
0 баллов: серьёзные или многочисленные ошибки, приводящие к неверному выводу.
4. Итоговый результат
1.
2.
3.
2 балла: чётко получено 000 (или иное искомое значение, если задача другая) и аргументировано, почему это именно так.
1 балл: ответ близок к правильному, но не доказано, либо отсутствует проверка.
0 баллов: итоговое значение неверно или вовсе не получено.
5. Структура и ясность записи
1.
2.
3.
2 балла: решение разбито по этапам; есть минимально необходимые пояснения, нет «скачков» между шагами.
1 балл: общий ход верен, но оформление страдает (сложно следить за логикой, часть шагов не пояснена).
0 баллов: работа выглядит как бессистемный набор выражений.
Суммируя баллы (максимум 10), педагог может выставить итоговую оценку и дать адресную обратную связь: на каком этапе
ученик ошибся или нуждается в более детальной проработке.
7.
Цель: проверить умение обучающихся применять тригонометрическиетождества для произведения косинусов, а также навыки грамотного
алгебраического упрощения с использованием базовых свойств синуса и
косинуса.
8.
Определение критериев9.
Выбор приёмов и формы оценивания• Приёмы:
• Использовать справочные таблицы тригонометрических
тождеств.
• Поощрять устный комментарий: «какой шаг и почему».
• Возможна самопроверка через подстановку конкретных
значений xxx (числовая проверка).
• Формы:
• Индивидуальная письменная работа
(контрольная/самостоятельная).
• Устный разбор у доски с поэтапной аргументацией.
10.
Для тренировки предлагаеманалогичные выражения, чтобы
учащиеся отработали разные
комбинации:
11.
Дескрипторы•Понимание задачи и подход (0–2)
•2 балла: ясно сформулировано, какие формулы планируется использовать, и почему.
•1 балл: частично указан метод или формула, но без пояснений.
•0 баллов: решение без понимания или с неправильным выбором формул.
•Тождества и их применение (0–2)
•2 балла: точное соблюдение формул
•1 балл: формулы в целом верные, но допущены мелкие ошибки (знаки, аргументы).
•0 баллов: неправильное использование тождества или путаница в формулах.
•Алгебраическая точность (0–2)
•2 балла: корректное упрощение
•1 балл: есть погрешности, но итог можно скорректировать.
•0 баллов: существенные ошибки, результат неверный.
•Ясность и логика (0–2)
•2 балла: решение по пунктам, каждый шаг понятен.
•1 балл: пропущена часть обоснований.
•0 баллов: ход решения не прослеживается.
•Получение итогового результата (0–2)
•2 балла: чёткое ответное выражение
•1 балл: результат почти получен, но не доведён или неверно оформлен.
•0 баллов: нет результата.
12.
13.
Формулировка цели оценивания• • Проверить умение использовать
тригонометрические тождества для нахождения
углов и функций.
• • Применять формулы половинного угла и другие
необходимые преобразования.
• • Выполнять алгебраические упрощения, включая
действия с радикалами.
• • Логично оформлять решение с соблюдением
математической корректности.
14.
Критерии оценивания (5критериев по 2 балла = 10)
1. Понимание условия и выбор метода (0–2)
2. Применение тригонометрических тождеств (0–2)
3. Алгебраическая точность (0–2)
4. Окончательный результат (0–2)
5. Логика и ясность оформления (0–2)
15.
Выбор приёмов и формыоценивания
• • Форма: индивидуальное письменное решение или
выступление у доски.
• • Приёмы:
– Использование справочных таблиц формул.
– Проверка приблизительных значений
(калькулятор).
– Рефлексия типичных ошибок в конце занятия.
16.
Разработка и подбор заданий• • Примерные тренировочные задачи:
17.
Дескрипторы оценивания1) Понимание условия: от полного до
отсутствующего (2–0).
2) Корректность тригонометрических тождеств: от
безупречных до неверных (2–0).
3) Алгебраические действия с корнями: от точных
до грубо ошибочных (2–0).
4) Итоговый результат совпадает с ответом.
ошибки (2–0).
5) Ясность оформления: аккуратно и логично vs.
хаотично (2–0).











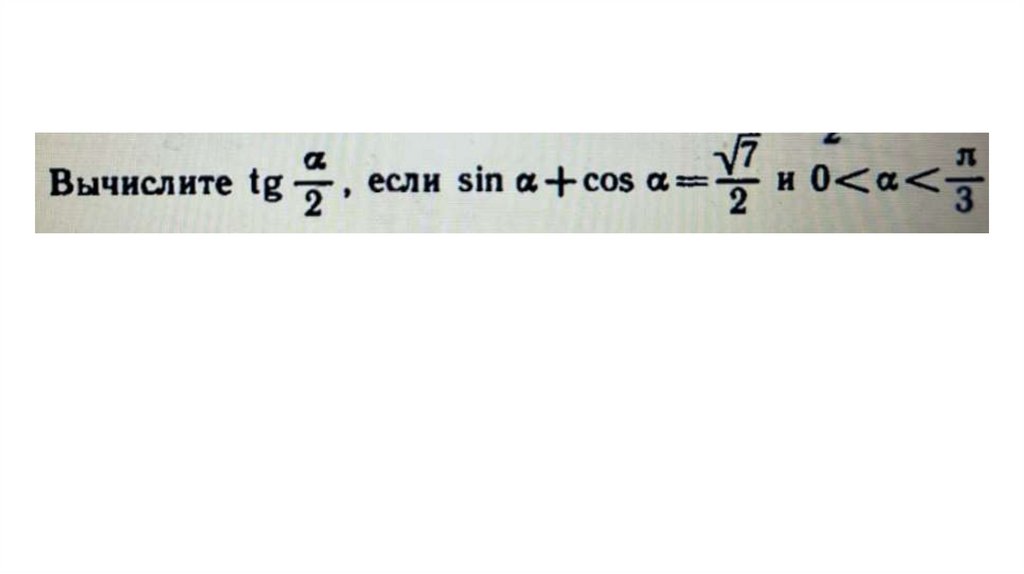





 mathematics
mathematics