Similar presentations:
Тригонометрические тождества
1.
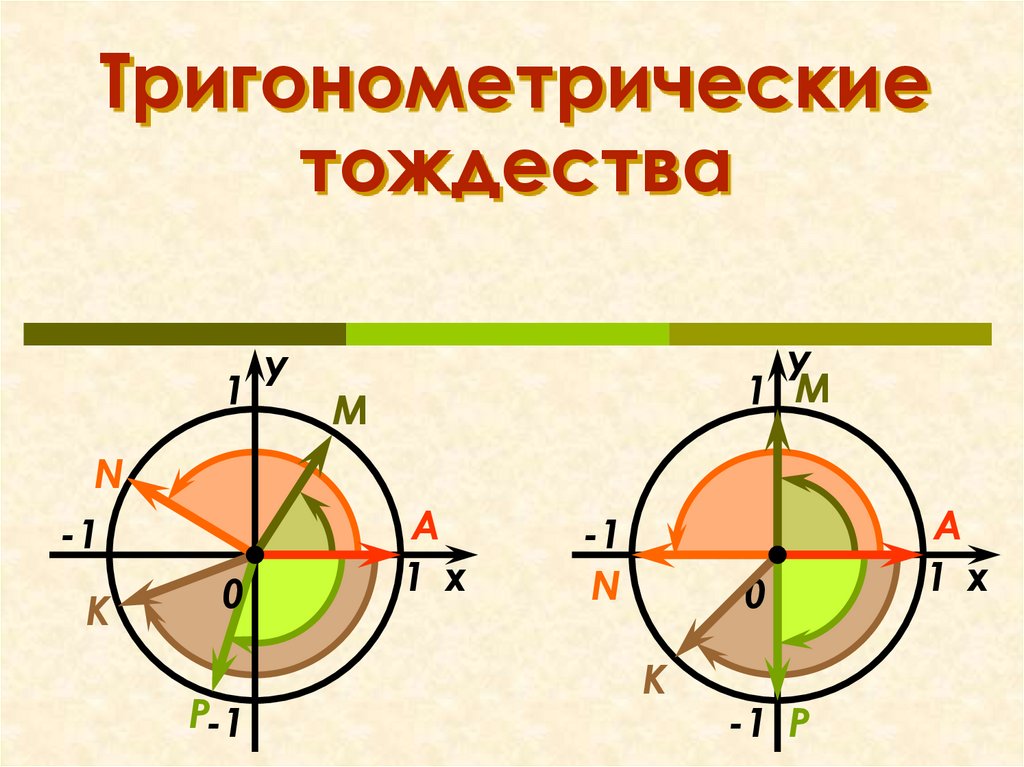
Тригонометрическиетождества
1
у
у
1 М
М
N
-1
K
0
P-1
А
1 x
-1
N
0
K
-1 P
А
1 x
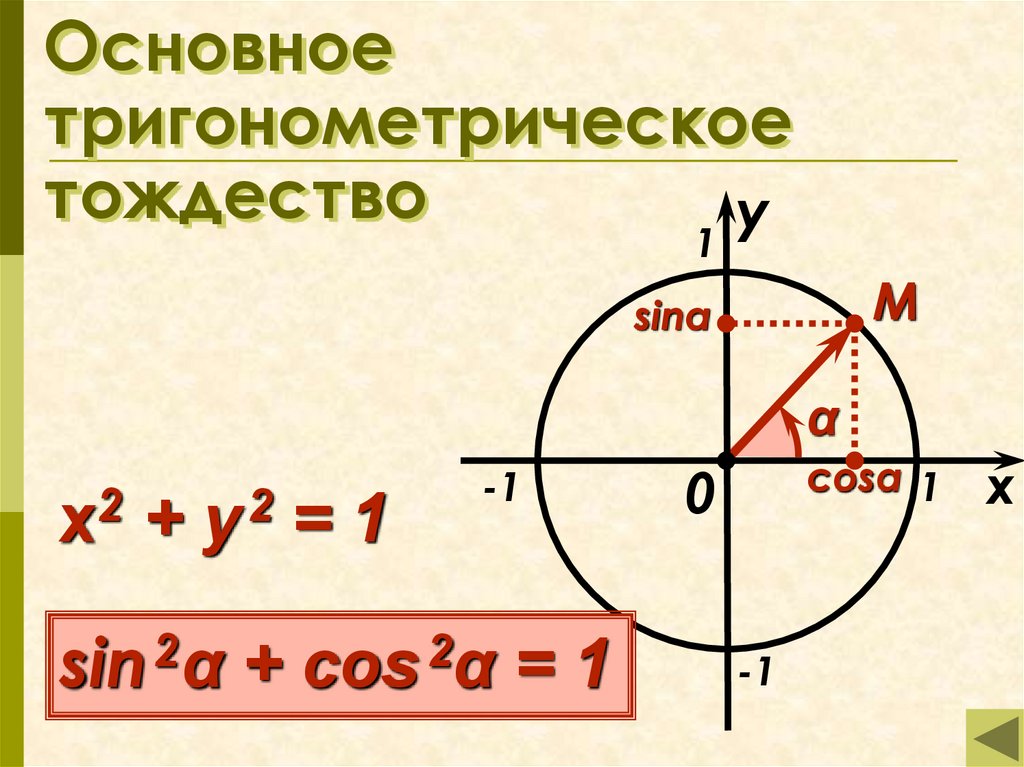
2. Основное тригонометрическое тождество
y1
M
sinα
α
2
x
+
2
y
=1
-1
sin 2α + cos 2α = 1
cosα 1
0
-1
x
3. Тригонометрическое тождество
sin2α+
cos2α
=1
:
2
cos α
sin2α cos2α
1
+
=
2
2
2
cos α cos α cos α
1
tg2α + 1 =
cos2α
4. Тригонометрическое тождество
sin2α+
cos2α
=1
:
2
sin α
sin2α cos2α
1
+
=
2
2
2
sin α sin α
sin α
1
1 + ctg2α =
sin2α
5. Тригонометрическое тождество
tgα x ctgα = 1sinα
cosα
x
=1
cosα
sinα
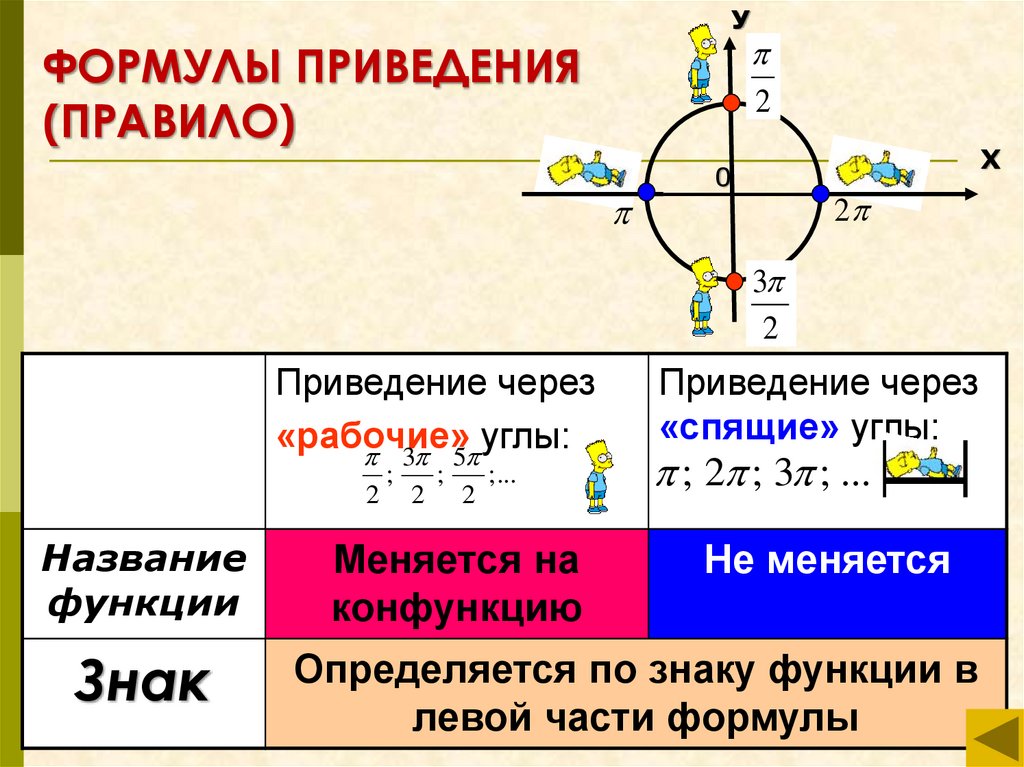
6. ФОРМУЛЫ ПРИВЕДЕНИЯ (ПРАВИЛО)
УФОРМУЛЫ ПРИВЕДЕНИЯ
(ПРАВИЛО)
2
Х
0
2
3
2
Приведение через
«рабочие»
углы:
3 5
2
Название
функции
Знак
;
2
;
2
; ...
Меняется на
конфункцию
Приведение через
«спящие» углы:
; 2 ; 3 ; ...
Не меняется
Определяется по знаку функции в
левой части формулы
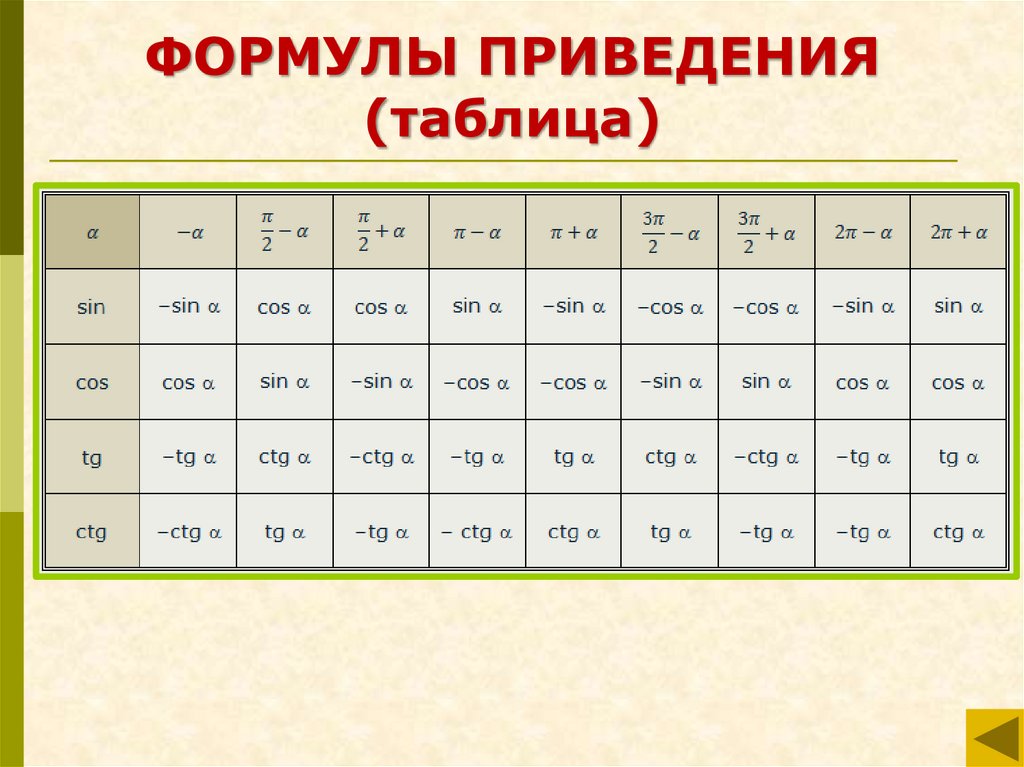
7.
ФОРМУЛЫ ПРИВЕДЕНИЯ(таблица)
8.
Формулы сложенияcos( ) cos cos sin sin
cos( ) cos cos sin sin
sin( ) sin cos cos sin
sin( ) sin cos cos sin
tg tg
tg ( )
1 tg tg
9.
Формулы суммы и разностиsin sin 2 sin
cos
2
2
sin sin 2 sin
cos
2
2
cos cos 2 cos
cos
2
2
cos cos 2 sin
sin
2
2
10.
Формулы суммы и разности11.
Формулы двойного аргументаsin 2 2sin cos
cos 2 cos sin
2
2
cos 2 1 2sin
2
cos 2 2 cos 1
2
2tg
tg 2
2
1 tg
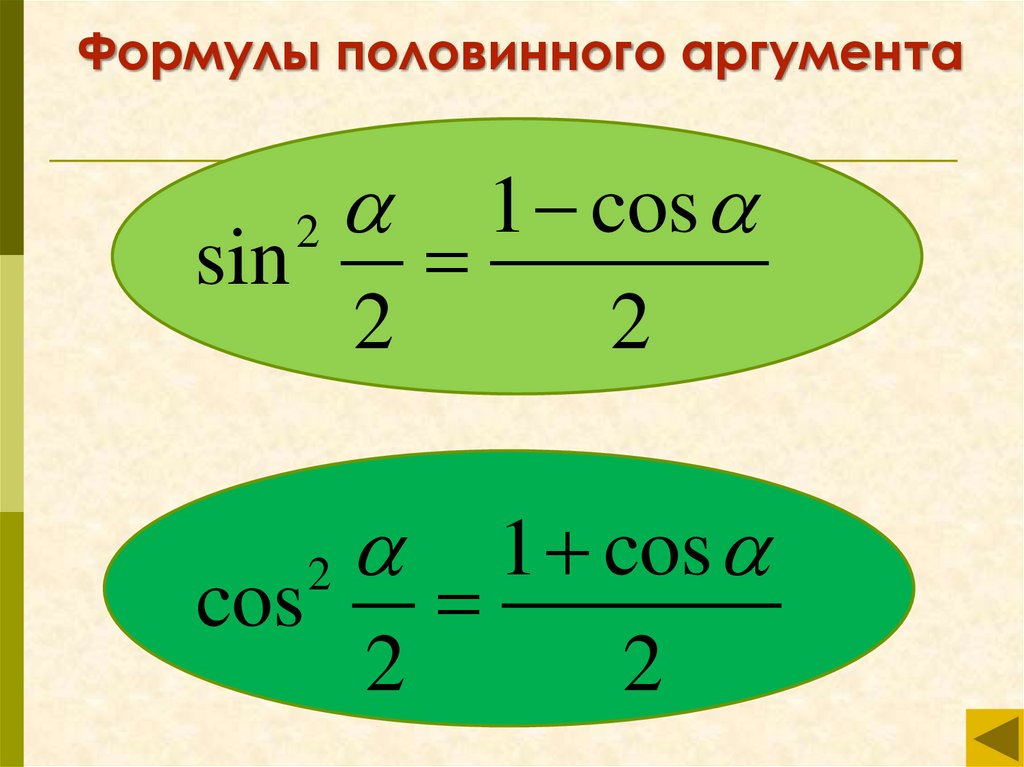
12.
Формулы половинного аргумента1 cos
sin
2
2
2
1 cos
cos
2
2
2
13.
Формулы преобразованияпроизведения в сумму
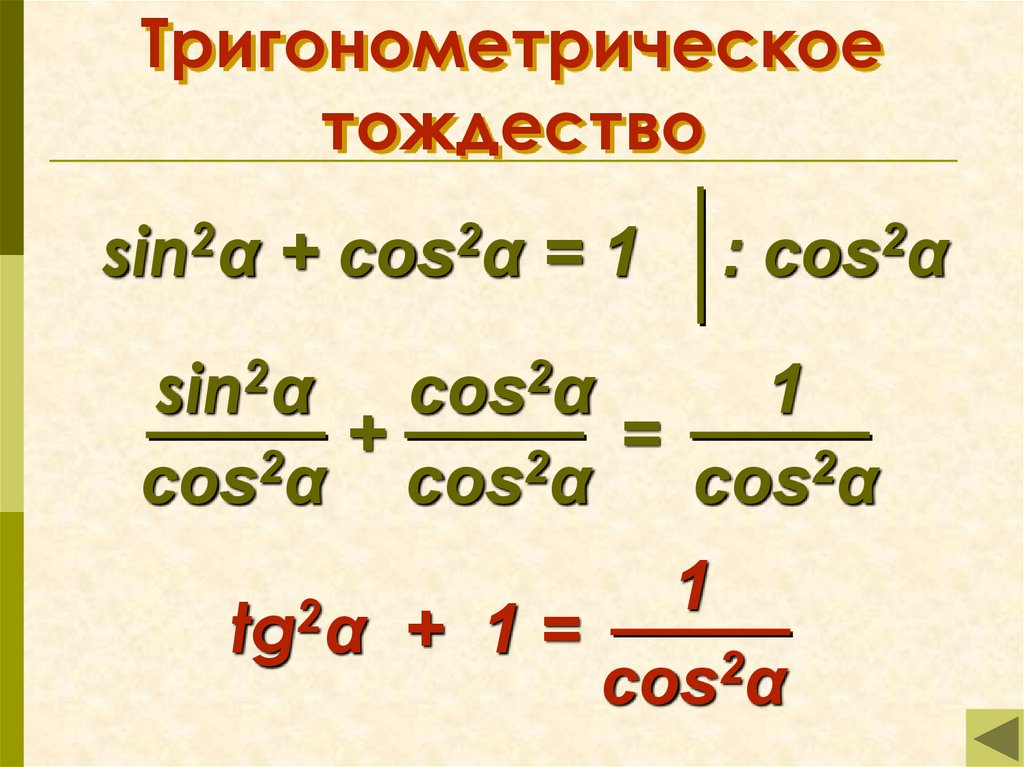







 mathematics
mathematics