Основные тригонометрические тождества. Решение задач

1.

Пускай кому- то мил английский,
Кому – то химия важна,
Без математики же всем нам
Но ни туда и ни сюда
Нам уравнения, как поэмы
А синусы поддерживают дух
Нам косинусы, будто песни,
А формулы тригонометрии
Ласкают слух!

2.

Тема урока:
“ Основные тригонометрические
тождества. Решение задач”.
Цель урока:
Знать:
Уметь:

3.

ЗНАЮ!
УМЕЮ!
РЕШУ!

4.

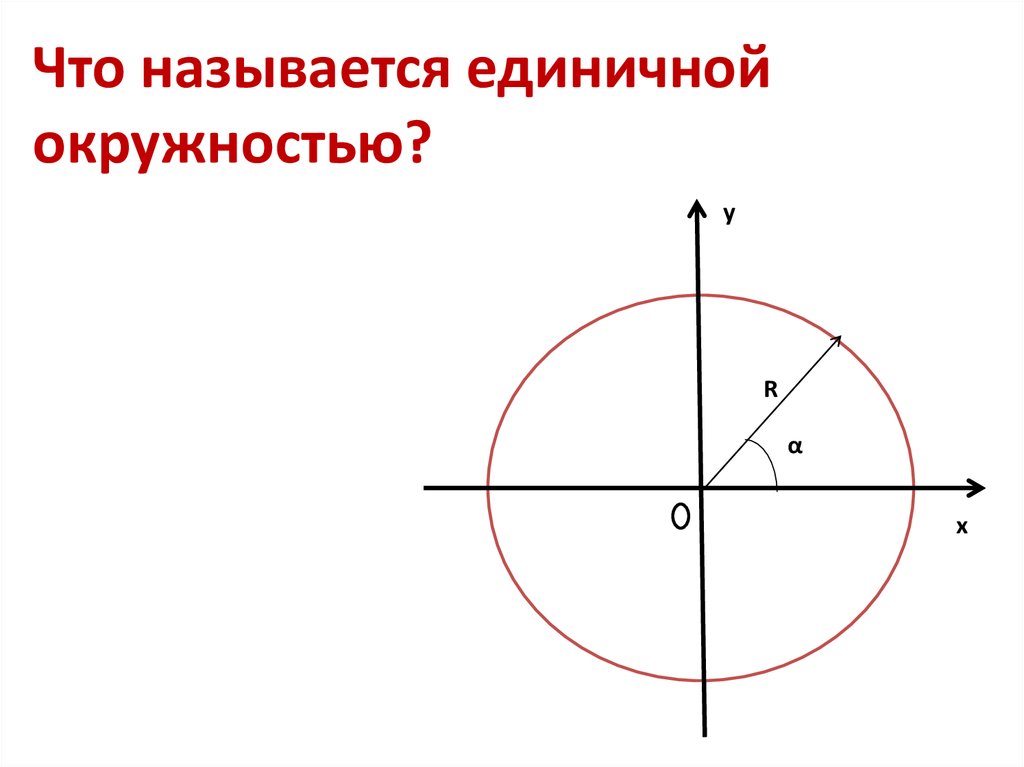
Что называется единичной
окружностью?
у
R
α
х

5.

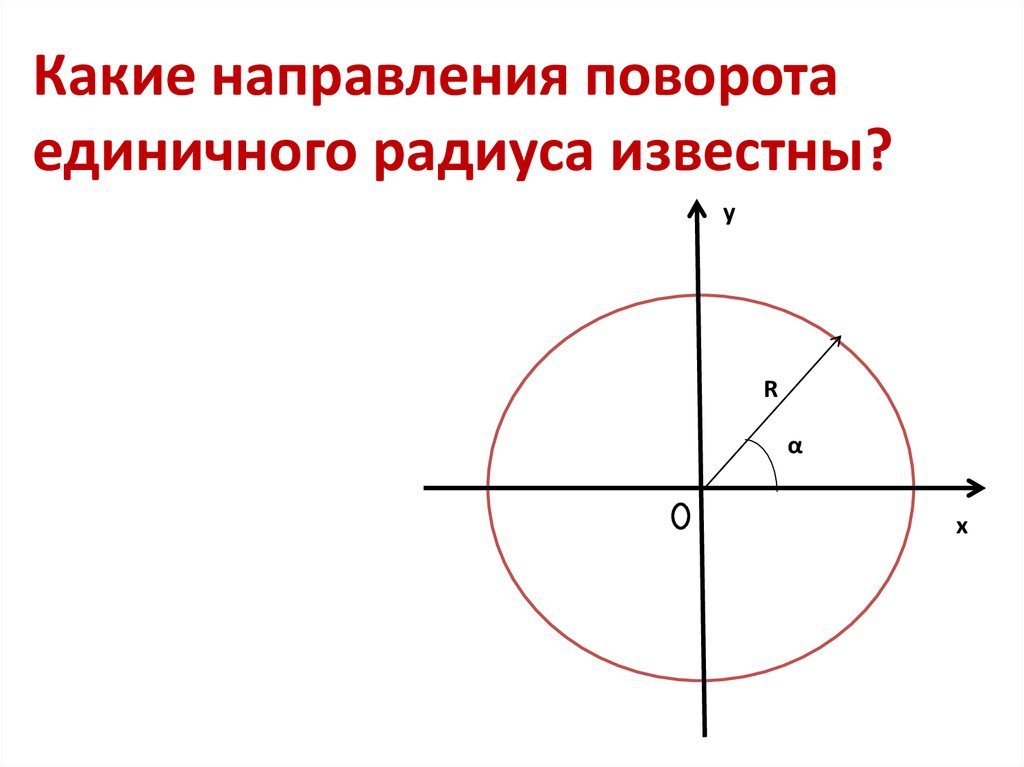
Какие направления поворота
единичного радиуса известны?
у
R
α
х

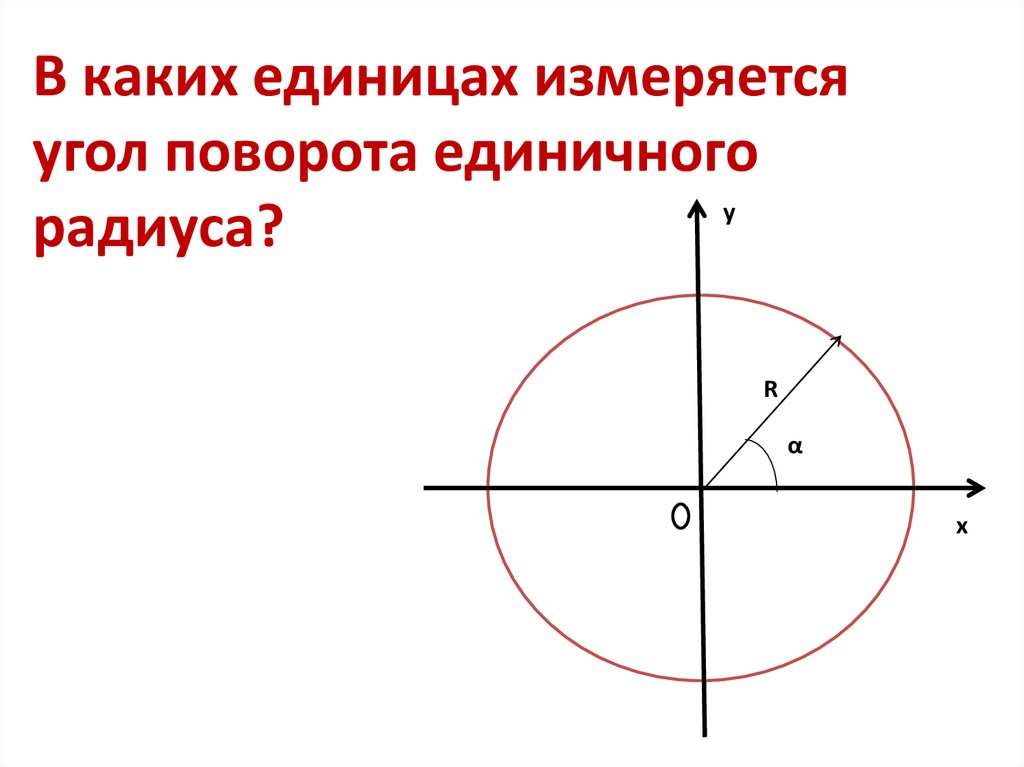
6.

В каких единицах измеряется
угол поворота единичного
у
радиуса?
R
α
х

7.

Что такое угол в один радиан?
Сколько приблизительно градусов
содержит угол в 1 радиан ? у
R
α
х

8.

Сформулируйте правила перевода
из градусной меры угла в
радианную меру и наоборот.

9.

Сформулируйте правила перевода
из градусной меры угла в
радианную меру и наоборот.
0
30
π
2
450
π
2π

10.

Какие тригонометрические
функции вы знаете?

11.

Какие тригонометрические
функции вы знаете?
От чего зависит значение
тригонометрических функций?

12.

Углом какой четверти является угол α , если:
α =15°
α =190°
α =100°

13.

Углом какой четверти является угол α , если:
α =-20°
α =-110°
α =289°

14.

Работа в группах
Правила работы в группе:
1.Группа совместно обсуждает и решает, выдвигает
идеи или опровергает их.
2.Каждый член группы должен работать в полную
меру своих сил.
3.Во время работы с уважением относитесь
к товарищам: принимая или отвергая идею, делайте
это вежливо. Помните, что каждый имеет право
на ошибку.
4.Помните, что успех группы зависит от того,
насколько каждый проявит свои достоинства.

15.

Работа в группах

16.

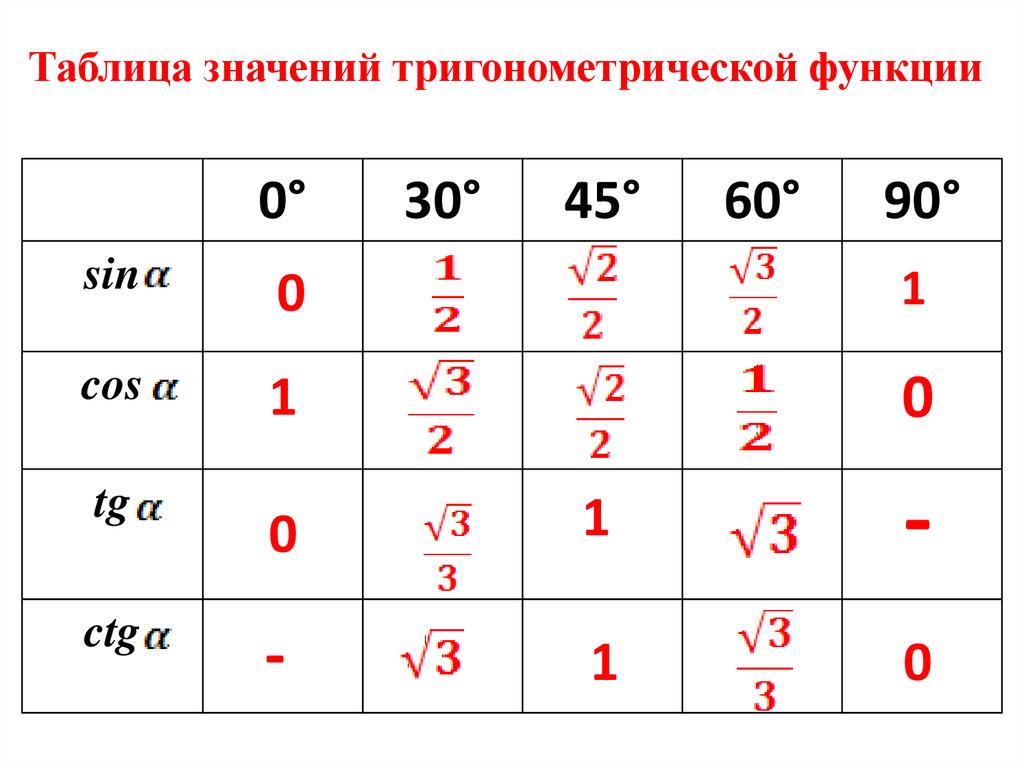
Таблица значений тригонометрической функции
0°
30°
45°
60°
90°
sin
0
1
cos
1
0
tg
ctg
0
1
-
-
1
0

17.

1
2
A
cos sin
2
2
2
B
3
sin 2 1
C
4
1 cos 2
D
5
1 tg
E
6
7
cos
2
1
ctg
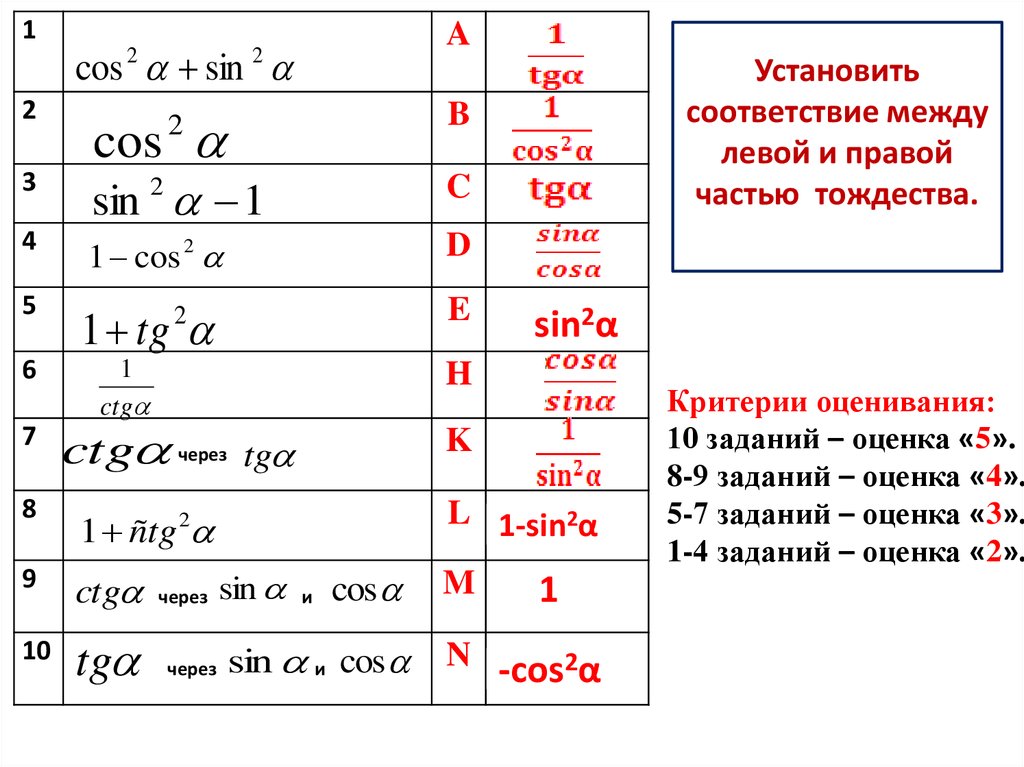
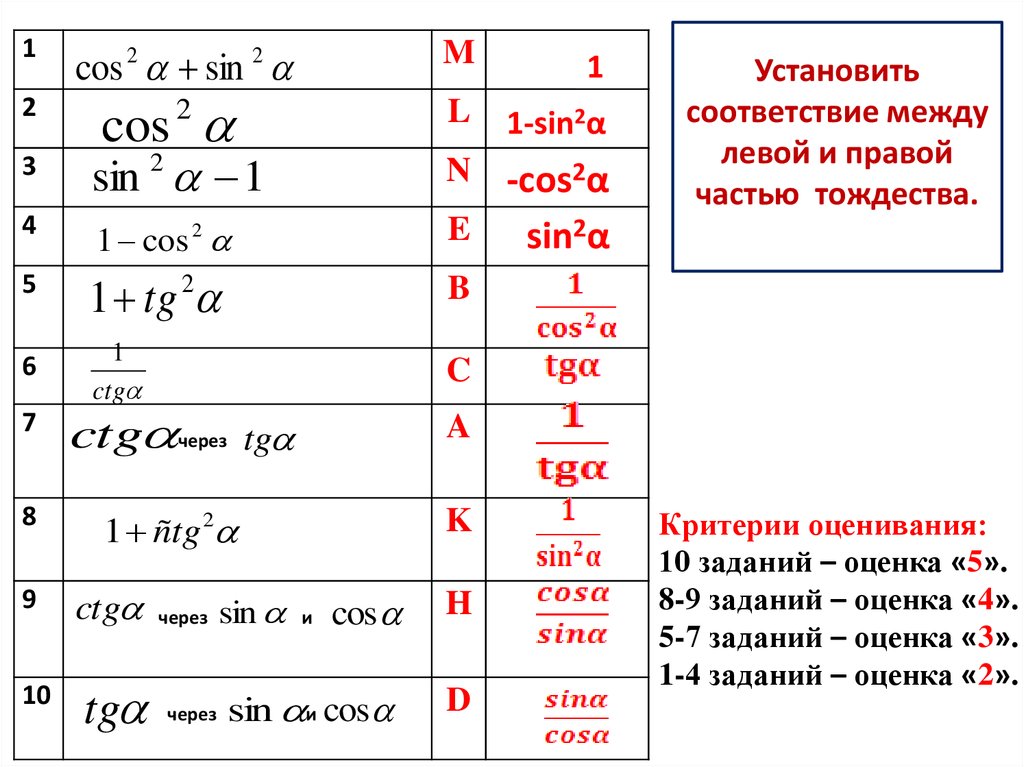
Установить
соответствие между
левой и правой
частью тождества.
sin2α
H
ctg через tg
8
1 ñtg 2
9
ctg
10
tg
через
через
K
L 1-sin2α
sin
и
cos
sin и cos
M
1
N -cos2α
Критерии оценивания:
10 заданий – оценка «5».
8-9 заданий – оценка «4».
5-7 заданий – оценка «3».
1-4 заданий – оценка «2».

18.

1
cos 2 sin 2
M
1
2
L
1-sin2α
3
sin 2 1
N
4
1 cos 2
-cos2α
E
sin2α
5
1 tg 2
B
6
1
ctg
C
2
7
8
cos
ctg через tg
A
1 ñtg 2
9
ctg
10
tg
через
через
K
cos
H
sin и cos
D
sin
Установить
соответствие между
левой и правой
частью тождества.
и
Критерии оценивания:
10 заданий – оценка «5».
8-9 заданий – оценка «4».
5-7 заданий – оценка «3».
1-4 заданий – оценка «2».

19.

Основное тригонометрическое тождество
2
2
cos sin 1
«тригонометрическая единица»

20.

Основное тригонометрическое тождество
2
2
cos sin 1
«тригонометрическая единица»
Косинус квадрат
Очень рад.
К нему едет брат
Синус квадрат!
Когда они встретятся
Окружность удивиться:
Выйдет целая семья,
То есть единица!

21.

Получите имя математика, в книге которого
впервые встречается термин –
1. 3 sin2 α+ 3 cos2 α
2. (1 – cos α)(1 + cos α) при α =90°
«тригонометрия».
3. 1- sin2 400
4. 2-2cos(-600)
5.
tgα∙ctgα
6. (ctg2α+ 1)(1 – sin2α)
7. tgα∙ctgα -1
8. cos2 α+ ctg2α+ sin2α
и
с
1
1
П
2
и
3
т
т
П
к
у
cos2 40°
3
ctg2α
0
4
и
5
с
6
к
7
у
8
с

22.

Питискус

23.

Аль-Батуни
Аль-Хорезми

24.

Бхаскара
Насиреддин
Туси

25.

Леонард Эйлер

26.

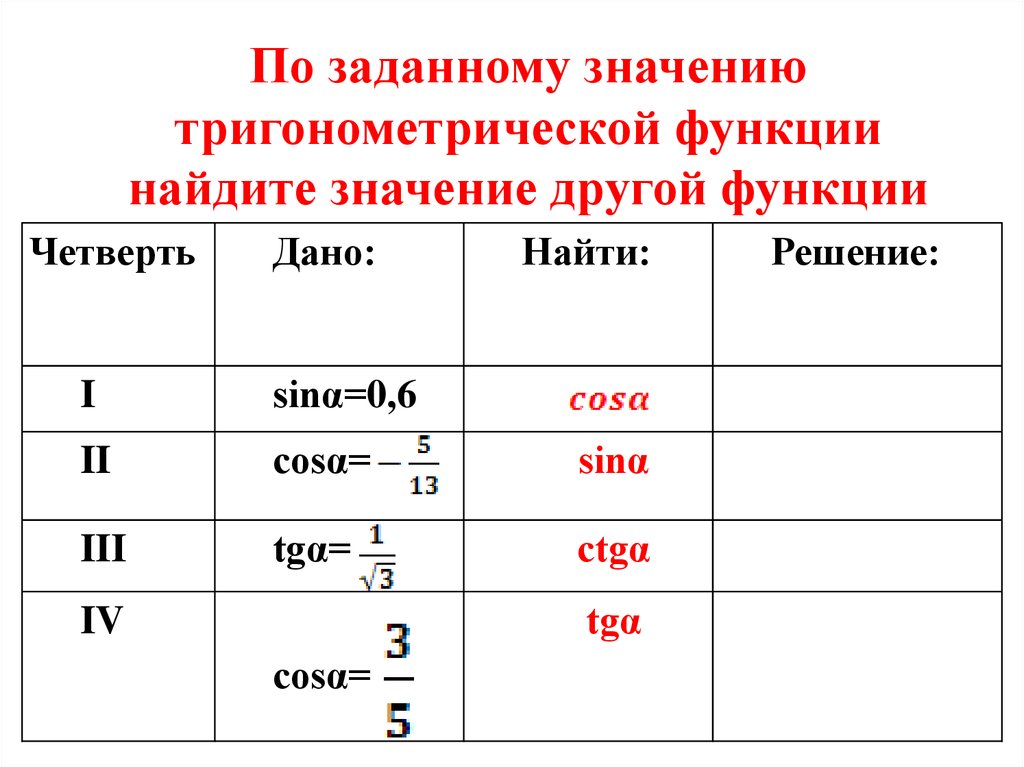
По заданному значению
тригонометрической функции
найдите значение другой функции
Четверть
Дано:
Найти:
I
sinα=0,6
II
cosα=
sinα
III
tgα=
ctgα
tgα
IV
cosα=
Решение:

27.

По заданному значению
тригонометрической функции
найдите значение другой функции
Четверть
I
Дано:
sinα=0,6
Найти:
Решение:

28.

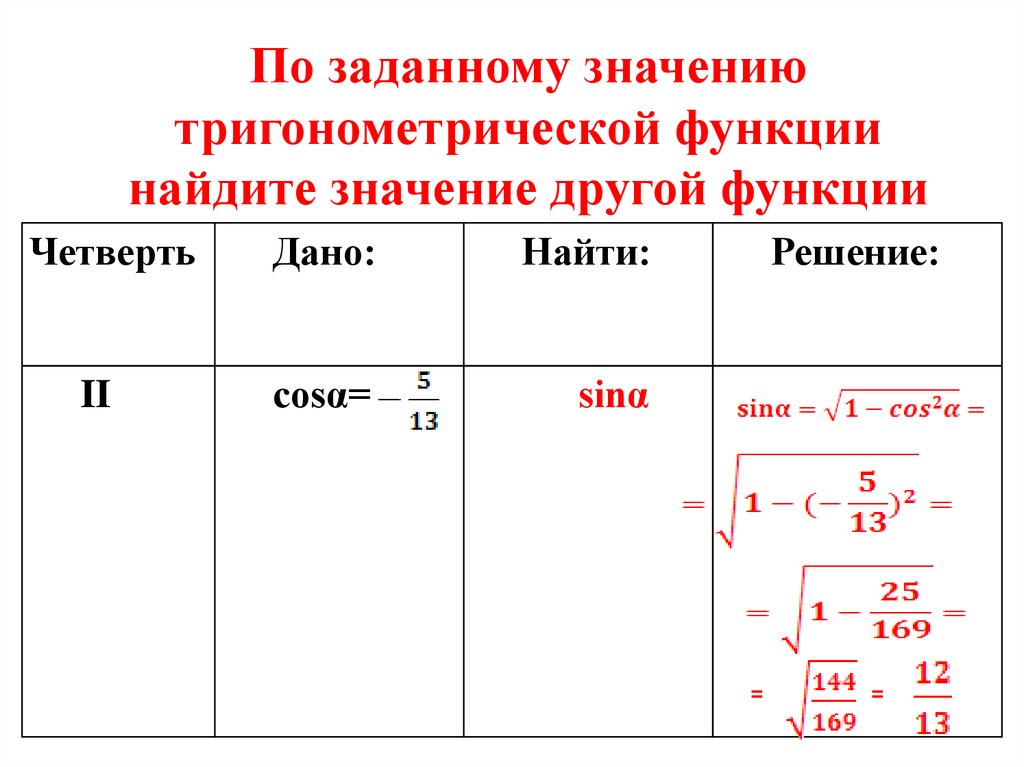
По заданному значению
тригонометрической функции
найдите значение другой функции
Четверть
II
Дано:
Найти:
cosα=
sinα
Решение:
=
=

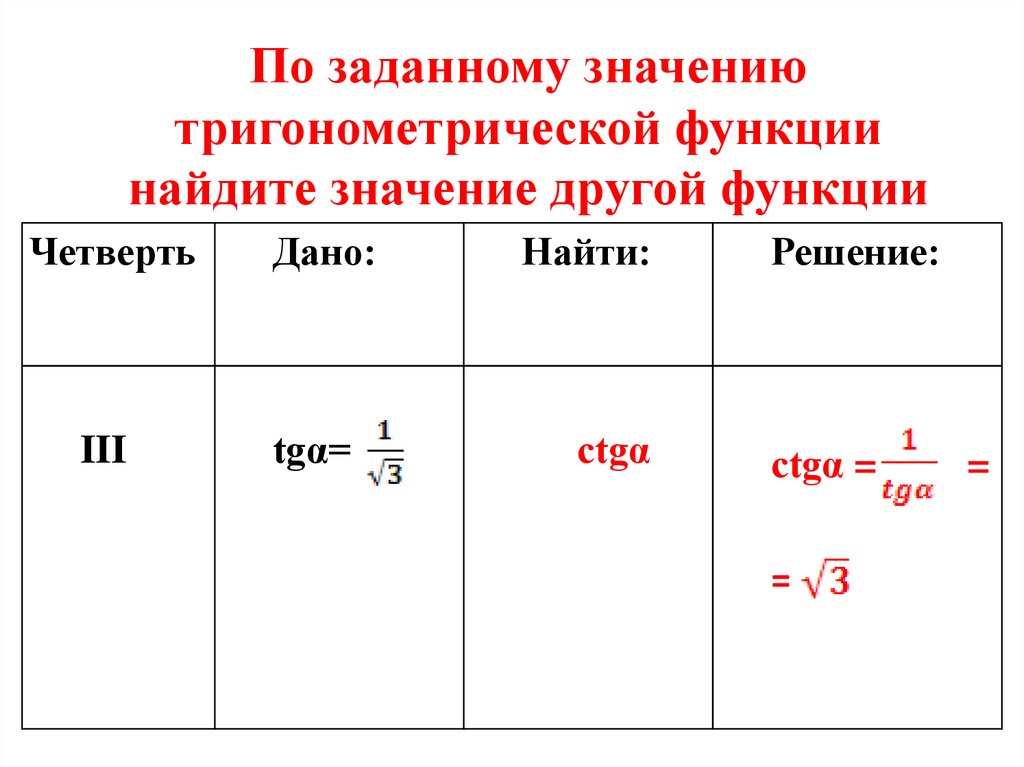
29.

По заданному значению
тригонометрической функции
найдите значение другой функции
Четверть
III
Дано:
tgα=
Найти:
ctgα
Решение:
ctgα =
=
=

30.

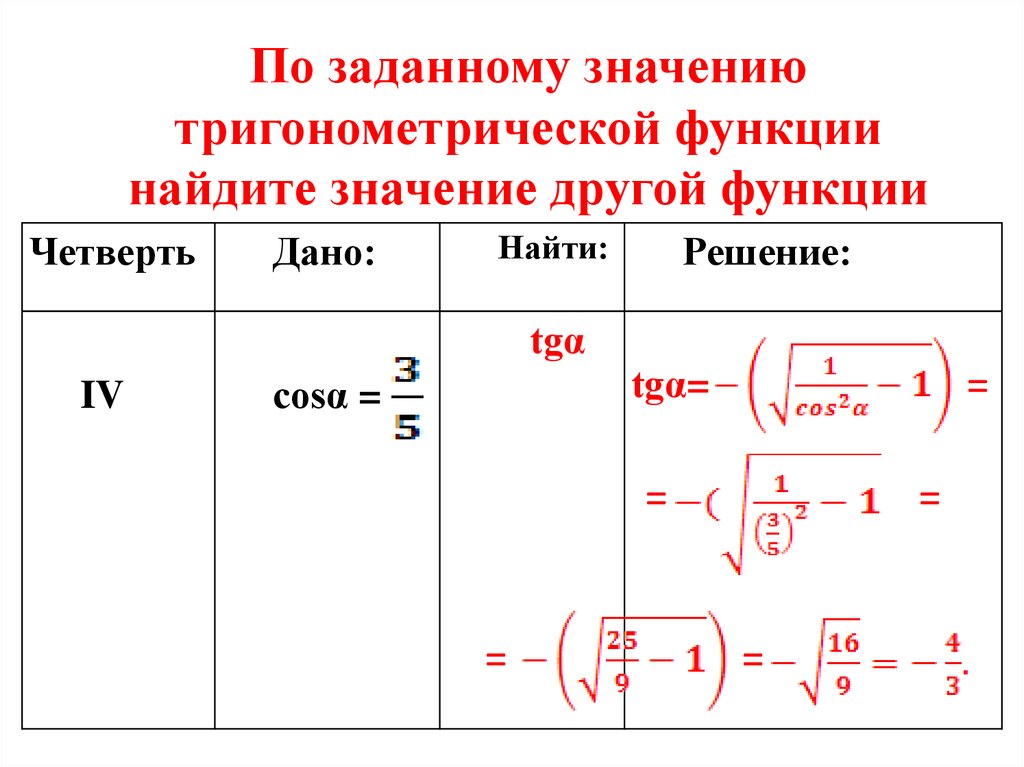
По заданному значению
тригонометрической функции
найдите значение другой функции
Четверть
Дано:
Найти:
tgα
IV
cosα =
Решение:
tgα=
=
=
=
=
=

31.

Применение тригонометрии в жизни человека.

32. Домашнее задание

•Сообщение:
«Тригонометрия в
жизни человека»
•№304 с.111

33.

y=sinx

34.

y=sinx
Спасибо за урок!

35.

Определите знак выражения
1 sin 240°
-
8
cos 290°
2 tg 98°
-
9
tg(-120°)
3 sin 70°
+
10 sin
4 ctg 200°
+
-
11 cos
-
12 cos
13 sin
+
+
+
14 tg
-
5 cos 113°
6 sin ( - 140° )
7 cos (-300° )
+
+
+